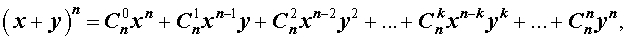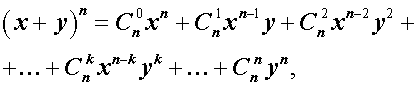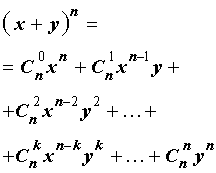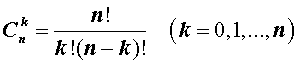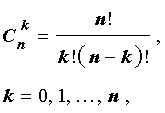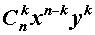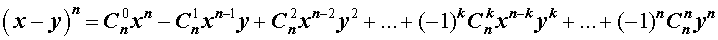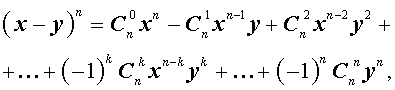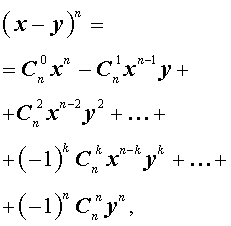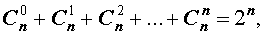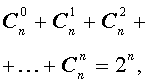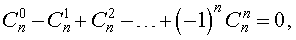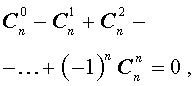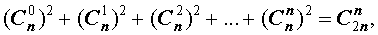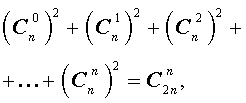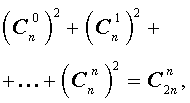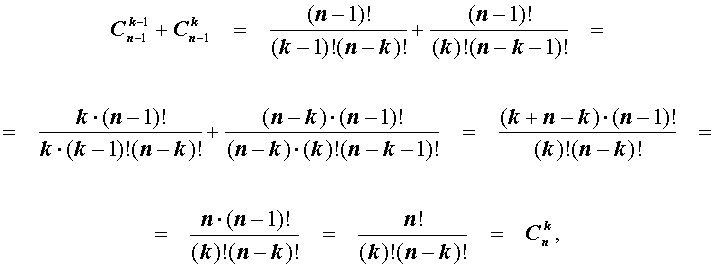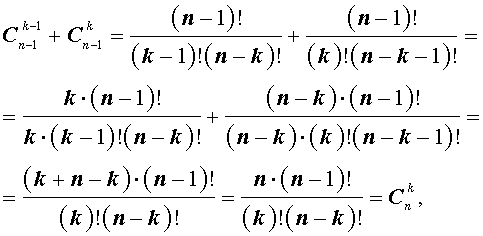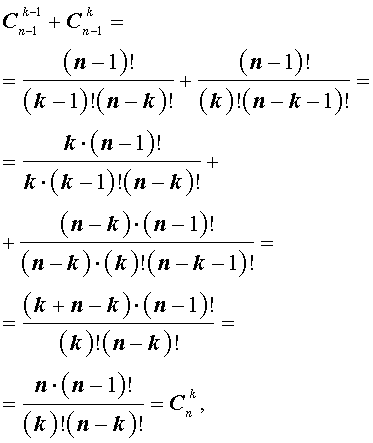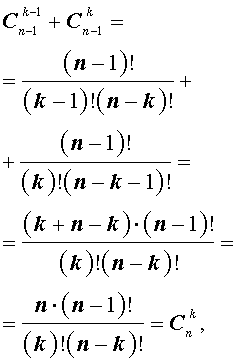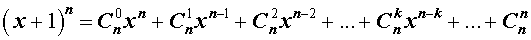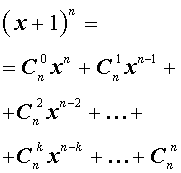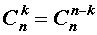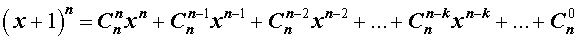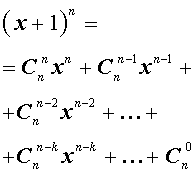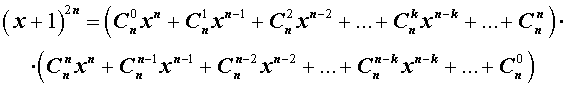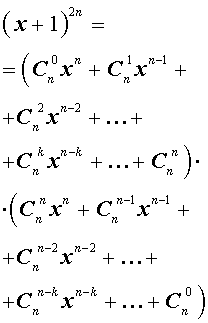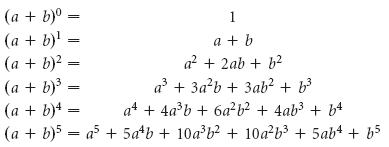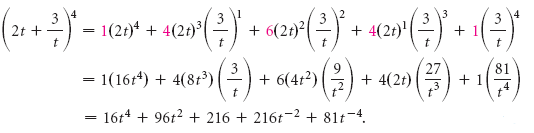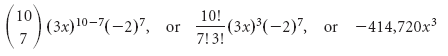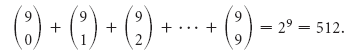Формула бинома Ньютона Формула бинома Ньютона |
 Связь бинома Ньютона с треугольником Паскаля Связь бинома Ньютона с треугольником Паскаля |
 Свойства биномиальных коэффициентов Свойства биномиальных коэффициентов |
- Формула бинома Ньютона
- Связь бинома Ньютона с треугольником Паскаля
- Свойства биномиальных коэффициентов
- Бином Ньютона
- Бином Ньютона — формула
- Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
- Доказательство формулы бинома Ньютона
- Бином Ньютона
- Биноминальное разложение с использованием треугольника Паскаля
- Бином Ньютона с использованием треугольника Паскаля
- Разложение бинома используя значения факториала
- Бином Ньютона с использованием обозначение факториала
- Нахождение определенного члена
- Нахождение (k + 1) члена
- Общее число подмножеств
- Полное число подмножеств
- 🎦 Видео
Видео:Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

Формула бинома Ньютона
В Таблице 1 из раздела «Формулы сокращенного умножения» приведены формулы для натуральных степеней бинома
в случаях, когда n = 1, 2, 3, 4, 5, 6.
В настоящем разделе рассматривается общий случай этой формулы, т.е. случай произвольного натурального значения n .
Утверждение . Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона :
– числа сочетаний из n элементов по k элементов.
В формуле (1) слагаемые
называют членами разложения бинома Ньютона , а числа сочетаний 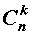
Если в формуле (1) заменить y на – y , то мы получим формулу для n — ой степени разности:
Видео:#219. БИНОМ НЬЮТОНА ДЛЯ ЧАЙНИКОВСкачать

Связь бинома Ньютона с треугольником Паскаля
Напомним, что треугольник Паскаля имеет следующий вид:
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
| № | Треугольник Паскаля |
| 0 | 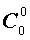 |
| 1 | 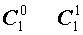 |
| 2 | 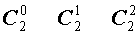 |
| 3 | 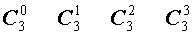 |
| 4 | 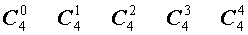 |
| 5 | 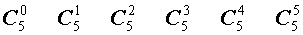 |
| 6 | 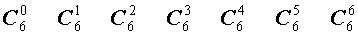 |
| … | … |
| Треугольник Паскаля |
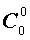 |
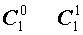 |
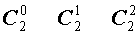 |
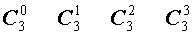 |
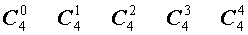 |
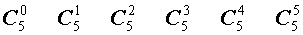 |
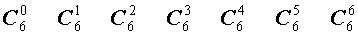 |
| … |
| Треугольник Паскаля |
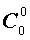 |
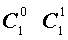 |
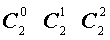 |
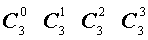 |
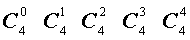 |
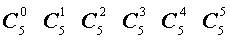 |
| … |
Видео:Треугольник ПаскаляСкачать

Свойства биномиальных коэффициентов
Для биномиальных коэффициентов справедливы равенства:
| 1 | 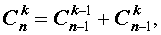 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Показатель степени | Биноминальные коэффициенты | ||||||||||
| 0 | C 0 0 | ||||||||||
| 1 | C 1 0 | C 1 1 | |||||||||
| 2 | C 2 0 | C 2 1 | C 2 2 | ||||||||
| 3 | C 3 0 | C 3 1 | C 3 2 | C 3 3 | |||||||
| ⋮ | … | … | … | … | … | … | … | … | … | ||
| n | C n 0 | C n 1 | … | … | … | … | … | C n n — 1 | C n n | ||
При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:
| Показатель степени | Биноминальные коэффициенты | ||||||||||||||
| 0 | 1 | ||||||||||||||
| 1 | 1 | 1 | |||||||||||||
| 2 | 1 | 2 | 1 | ||||||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| ⋮ | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| n | C n 0 | C n 1 | … | … | … | … | … | … | … | … | … | C n n — 1 | C n n | ||
Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.
Видео:БИНОМ Ньютона | треугольник ПаскаляСкачать

Доказательство формулы бинома Ньютона
Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:
- коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле C n p = C n n — p , где р = 0 , 1 , 2 , … , n ;
- C n p = C n p + 1 = C n + 1 p + 1 ;
- биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть C n 0 + C n 1 + C n 2 + . . . + C n n = 2 n ;
- при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.
Равенство вида a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n считается справедливым. Докажем его существование.
Для этого необходимо применить метод математической индукции.
Для доказательства необходимо выполнить несколько пунктов:
- Проверка справедливости разложения при n = 3 . Имеем, что
a + b 3 = a + b a + b a + b = a 2 + a b + b a + b 2 a + b = = a 2 + 2 a b + b 2 a + b = a 3 + 2 a 2 b + a b 2 + a 2 b + 2 a b + b 3 = = a 3 + 3 a 2 b + 3 a b 2 + b 3 = C 3 0 a 3 + C 3 1 a 2 b + C 3 2 a b 2 + C 3 3 b 3 - Если неравенство верно при n — 1 , тогда выражение вида a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1
- Доказательство равенства a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1 , основываясь на 2 пункте.
Доказательство 1
a + b n = a + b a + b n — 1 = = ( a + b ) C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1
Необходимо раскрыть скобки, тогда получим a + b n = C n — 1 0 · a n + C n — 1 1 · a n — 1 · b + C n — 1 2 · a n — 2 · b 2 + . . . + C n — 1 n — 2 · a 2 · b n — 2 + + C n — 1 n — 1 · a · b n — 1 + C n — 1 0 · a n — 1 · b + C n — 1 1 · a n — 2 · b 2 + C n — 1 2 · a n — 3 · b 3 + . . . + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n
Производим группировку слагаемых
a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n
Имеем, что C n — 1 0 = 1 и C n 0 = 1 , тогда C n — 1 0 = C n 0 . Если C n — 1 n — 1 = 1 и C n n = 1 , тогда C n — 1 n — 1 = C n n . При применении свойства сочетаний C n p + C n p + 1 = C n + 1 p + 1 , получаем выражение вида
C n — 1 1 + C n — 1 0 = C n 1 C n — 1 2 + C n — 1 1 = C n 2 ⋮ C n — 1 n — 1 + C n — 1 n — 2 = C n n — 1
Произведем подстановку в полученное равенство. Получим, что
a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 = C n — 1 n — 1 · b n
После чего можно переходить к биному Ньютона, тогда a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n .
Видео:ТРЕУГОЛЬНИК ПАСКАЛЯ 😊 ЧАСТЬ I #shorts #математика #егэ #задачи #задачаналогику #егэ2022 #огэ2022Скачать

Бином Ньютона
Биноминальное разложение с использованием треугольника Паскаля
Рассмотрим следующие выражения со степенями (a + b) n , где a + b есть любой бином, а n — целое число.
Каждое выражение — это полином. Во всех выражениях можно заметить особенности.
1. В каждом выражении на одно слагаемое больше, чем показатель степени n.
2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.
3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до «половины пути», а потом уменьшаются на те же значения обратно к 1.
Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b) 6 . Согласно особенности, которую мы только что заметили, здесь должно быть 7 членов
a 6 + c1a 5 b + c2a 4 b 2 + c3a 3 b 3 + c4a 2 b 4 + c5ab 5 + b 6 .
Но как мы можем определить значение каждого коэффициента, ci? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля:
Есть много особенностей в треугольнике. Найдите столько, сколько сможете.
Возможно вы нашли путь, как записать следующую строку чисел, используя числа в строке выше. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b) 6 путем добавления следующей строки, используя особенности, которые мы нашли:
Мы видим, что в последней строке
первой и последнее числа 1;
второе число равно 1 + 5, или 6;
третье число это 5 + 10, или 15;
четвертое число это 10 + 10, или 20;
пятое число это 10 + 5, или 15; и
шестое число это 5 + 1, или 6.
Таким образом, выражение (a + b) 6 будет равно
(a + b) 6 = 1a 6 + 6a 5 b + 15a 4 b 2 + 20a 3 b 3 + 15a 2 b 4 + 6ab 5 + 1b 6 .
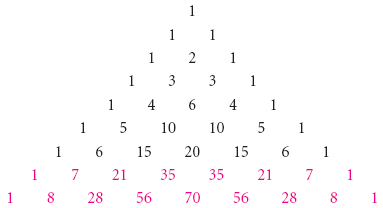
Для того, чтобы возвести в степень (a + b) 8 , мы дополняем две строки к треугольнику Паскаля:
Тогда
(a + b) 8 = a 8 + 8a 7 b + 28a 6 b 2 + 56a 5 b 3 + 70a 4 b 4 + 56a 3 b 5 + 28a 2 b 6 + 8ab 7 + b 8 .
Мы можем обобщить наши результаты следующим образом.
Бином Ньютона с использованием треугольника Паскаля
Для любого бинома a+ b и любого натурального числа n,
(a + b) n = c0a n b 0 + c1a n-1 b 1 + c2a n-2 b 2 + . + cn-1a 1 b n-1 + cna 0 b n ,
где числа c0, c1, c2. cn-1, cn взяты с (n + 1) ряда треугольника Паскаля.
Пример 1 Возведите в степень: (u — v) 5 .
Решение У нас есть (a + b) n , где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:
1 5 10 10 5 1
Тогда у нас есть
(u — v) 5 = [u + (-v)] 5 = 1(u) 5 + 5(u) 4 (-v) 1 + 10(u) 3 (-v) 2 + 10(u) 2 (-v) 3 + 5(u)(-v) 4 + 1(-v) 5 = u 5 — 5u 4 v + 10u 3 v 2 — 10u 2 v 3 + 5uv 4 — v 5 .
Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.
Пример 2 Возведите в степень: (2t + 3/t) 4 .
Решение У нас есть (a + b) n , где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:
1 4 6 4 1
Тогда мы имеем
Разложение бинома используя значения факториала
Предположим, что мы хотим найти значение (a + b) 11 . Недостаток в использовании треугольника Паскаля в том, что мы должны вычислить все предыдущие строки треугольника, чтобы получить необходимый ряд. Следующий метод позволяет избежать этого. Он также позволяет найти определенную строку — скажем, 8-ю строку — без вычисления всех других строк. Этот метод полезен в вычислениях, статистике и он использует биномиальное обозначение коэффициента 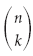
Мы можем сформулировать бином Ньютона следующим образом.
Бином Ньютона с использованием обозначение факториала
Для любого бинома (a + b) и любого натурального числа n,
Бином Ньютона может быть доказан методом математической индукции. Она показывает почему 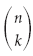
Пример 3 Возведите в степень: (x 2 — 2y) 5 .
Решение У нас есть (a + b) n , где a = x 2 , b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем 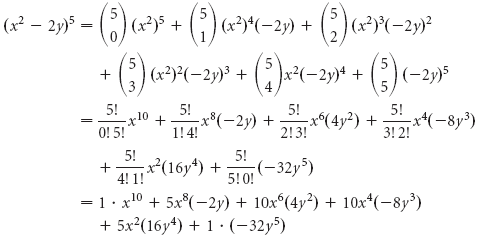
Наконец, (x 2 — 2y) 5 = x 10 — 10x 8 y + 40x 6 y 2 — 80x 4 y 3 + 80x 2 y 4 — 35y 5 .
Пример 4 Возведите в степень: (2/x + 3√ x ) 4 .
Решение У нас есть (a + b) n , где a = 2/x, b = 3√ x , и n = 4. Тогда, используя бином Ньютона, мы получим
Finally (2/x + 3√ x ) 4 = 16/x 4 + 96/x 5/2 + 216/x + 216x 1/2 + 81x 2 .
Нахождение определенного члена
Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.
Обратите внимание, что в биноме Ньютона 
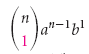

Нахождение (k + 1) члена
(k + 1) член выражения (a + b) n есть 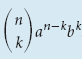
Пример 5 Найдите 5-й член в выражении (2x — 5y) 6 .
Решение Во-первых, отмечаем, что 5 = 4 + 1. Тогда k = 4, a = 2x, b = -5y, и n = 6. Тогда 5-й член выражения будет
Пример 6 Найдите 8-й член в выражении (3x — 2) 10 .
Решение Во-первых, отмечаем, что 8 = 7 + 1. Тогда k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член выражения будет
Общее число подмножеств
Предположим, что множество имеет n объектов. Число подмножеств, содержащих k элементов есть 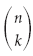

Теперь давайте рассмотрим возведение в степень (1 + 1) n :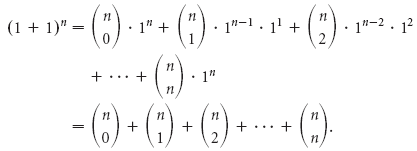
Так. общее количество подмножеств (1 + 1) n , или 2 n . Мы доказали следующее.
Полное число подмножеств
Полное число подмножеств множества с n элементами равно 2 n .
Пример 7 Сколько подмножеств имеет множество ?
Решение Множество имеет 5 элементов, тогда число подмножеств равно 2 5 , или 32.
Пример 8 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:
<кетчуп, горчица, майонез, помидоры, салат, лук, грибы, оливки, сыр>.
Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?
Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно
. Таким образом, Венди может предложить 512 различных гамбургеров.
🎦 Видео
Бином Ньютона. 10 класс.Скачать

Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)Скачать

Высшая математика для детей 6+Скачать

Бином Ньютона и его свойства. 9 класс.Скачать

Треугольник Паскаля Python. Коэффициенты для Бинома НьютонаСкачать

Бином Ньютона: формула, доказательство и Треугольник ПаскаляСкачать

Бином НьютонаСкачать

Бином Ньютона.Треугольник Паскаля.Скачать

✓ Бином Ньютона. Игра в слова. Числа сочетаний | Комбинаторика | Ботай со мной #057 | Борис ТрушинСкачать

Бином Ньютона. Практическая часть. 10 класс.Скачать

Несколько красивых свойств треугольника ПаскаляСкачать
Треугольник Паскаля. Бином НьютонаСкачать