Вопрос по математике:
Точка О – центр вписанной в треугольник АВС окружности. К
плоскости данного треугольника проведен перпендикуляр ОК.
Найдите расстояние от точки К до сторон треугольника, если
АВ=ВС=30 см., АС=36 см., ОК=18 см.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать
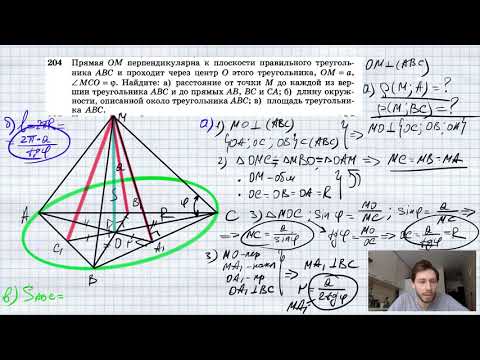
Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярная к плоскости треугольника. Найдите
Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Ваш ответ
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

решение вопроса
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,061
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Задание 16. ЕГЭ. Точка О – центр вписанной в треугольник АВС окружности.
Задание. Точка О – центр вписанной в треугольник АВС окружности. Прямая ВО вторично пересекает описанную около этого треугольника окружность в точке Е.
а) Докажите, что ∠ЕОС = ∠ЕСО.
б) Найдите площадь треугольника АСЕ, если радиус описанной около треугольника АВС окружности равен 6√3, ∠АВС = 60 0 .
Решение:
а) Докажите, что ∠ЕОС = ∠ЕСО.
Так как точка О – центр вписанной в треугольник ΔАВС окружности, то она является точкой пересечения биссектрис CО, ВО и AО треугольника ΔАВС.
Угол ∠ЕОС – внешний угол треугольника ΔВОС, тогда ∠ЕОС равен сумме двух углов треугольника ΔВOС, не смежных с ним, т. е.
∠ЕОС = ∠ВСО + ∠СВО
Так как СО – биссектриса угла ∠С треугольника ΔАВС, то
Так как BО – биссектриса угла ∠B треугольника ΔАВС, то
Угол ∠ECО равен: ∠ECО = ∠АСO + ∠ECA
Угол ∠АСO = ∠ВCО (CО – биссектриса).
Угол ∠ECA – вписанный в окружность угол, который опирается на дугу ᴗAE.
На дугу ᴗAE также опирается угол ∠AВE = ∠CВO (BО – биссектриса).
Значит, ∠ECО = ∠ВCО + ∠CBО, т.е.
Следовательно, ∠ЕОС = ∠ЕСО.
б) Найдите площадь треугольника АСЕ, если радиус описанной около треугольника АВС окружности равен 6√3, ∠АВС = 60 0 .
Около треугольника ΔCВE описана окружность с радиусом R = 6√3 и ∠CВE =∠CВО = 30 0 , тогда для треугольника ΔCBE справедливо равенство
Угол ∠CBE – вписанный в окружность угол, который опирается на дугу ᴗCE,
угол ∠EВA – вписанный в окружность угол, который опирается на дугу ᴗAE.
Так как ∠СВЕ = ∠ЕВА, то ᴗCE = ᴗAE и хорды СЕ и АЕ равны, т. е. СЕ = АЕ = 6√3.
Угол ∠АBС = 60 0 – вписанный в окружность угол, который опирается на дугу ᴗАEС и ᴗАEС = 120 0 .
Значит, дуга ᴗАВС = 360 0 — ᴗАEС = 360 0 – 120 0 = 240 0 .
Угол ∠АЕС – вписанный в окружность угол равен половине дуги ᴗАВC, на которую он опирается, т. е. угол ∠АЕС = 120 0 .
Площадь треугольника ΔАСЕ равна
Ответ: 27√3
🎦 Видео
Построить описанную окружность (Задача 1)Скачать

2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать

Геометрия В треугольнике ABC точка O – центр описанной окружности, точка L – середина стороны ABСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Вариант #19 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать

№213. Правильные треугольники ABC и DBC расположены так, что вершина D проектируется в центр треуголСкачать

✓ Спидран: Красивая олимпиадная планиметрия за 5 минут | Осторожно, спойлер! | Борис ТрушинСкачать

✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

Как найти центр круга в мастерской (4 способа)Скачать

Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать
