Теорема прямоугольного треугольника 30

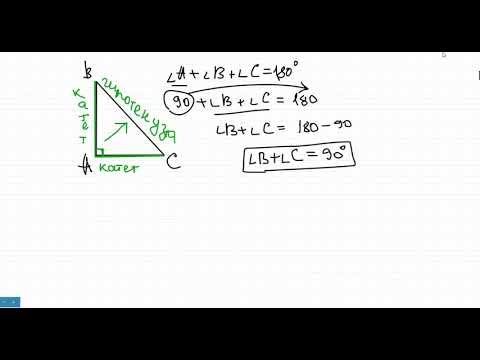
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Свойство катета прямоугольного треугольника, лежащего против угла в 30° с примерами

Свойство катета прямоугольного треугольника, лежащего против угла в 30°:

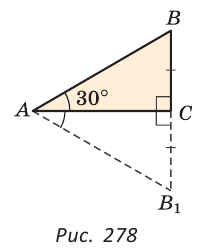
Теорема (о катете, лежащем против угла в 30°). Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

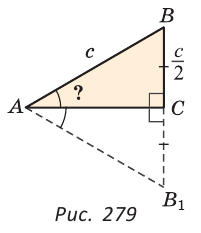
Дано:

Доказать: ВС = 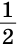АВ.

Доказательство:

На луче ВС отложим отрезок СВ₁ равный отрезку ВС. Так как АВ₁С =АВС по двум катетам (катет АС — общий), то B₁AC =BAC = 30°,

BAB₁ = 60°. Но В = В₁ = 60°. Известно, что если у треугольника все углы равны, то он равносторонний. Отсюда АВВ₁ — равносторонний, АВ = ВВ₁, ВС = ВВ₁ =АВ. Теорема доказана.

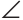
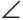
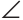
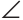
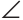
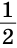
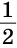
Верно и утверждение, обратное данному. Докажем его.

Теорема. Если в прямоугольном треугольнике катет равен половине гипотенузы, то этот катет лежит против угла в 30°.

Доказательство:

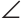
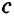
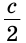
Пусть в треугольнике ABC C = 90°, АВ = , ВС= (рис. 279).

Докажем, что BAC = 30°. Продлим катет ВС на его длину: СВ₁ = ВС. Из равенства прямоугольных треугольников АСВ₁ и АСВ (по двум катетам) следует, что АВ₁ = АВ = ВВ₁ = . Значит, АВВ₁ — равносторонний, все его углы равны по 60°, а его высота АС является биссектрисой. Поэтому BAC = 30°. Что и требовалось доказать.

Пример:

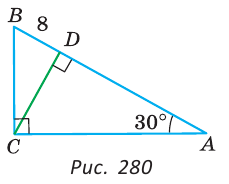
В прямоугольном треугольнике ABC, у которого C = 90°, A=30°, проведена высота CD. Найти отрезок AD, если BD = 8 см.

Решение:

Так как угол А и угол BCD дополняют угол В до 90°, то BCD=A=30° (рис. 280).

В прямоугольном треугольнике CDB катет BD лежит против угла в 30°. Поэтому СВ = 2BD = 16 см.

В треугольнике ABC катет ВС лежит против угла в 30°. Поэтому АВ = 2ВС = 32 см.

Отсюда AD=AB-BD = 32 — 8 = 24 (см).

Замечание. Мы доказали, что BC = 2BD, AB = 2BC = 4BD, AD = АВ — BD = 3BD, то есть в прямоугольном треугольнике с углом 30° высота делит гипотенузу в отношении 1 : 3.

Пример:

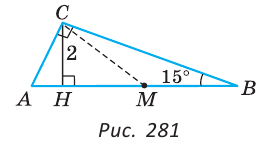
Дан прямоугольный треугольник с углом 15°. Высота, проведенная к гипотенузе, равна 2 см. Найти гипотенузу.

Решение:

Пусть в треугольнике ABC ACB = 90°, B = 15°, СН = 2 см — высота (рис. 281).

Нужно найти АВ. Проведем медиану СМ треугольника ABC. Так как в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы, то СМ = MB. Треугольник СМВ — равнобедренный, MCB = CBM = 15°, AMC — его внешний угол.

По свойству внешнего угла AMC =MCB +MBC = 15° + 15° = 30°.

В прямоугольном треугольнике СНМ катет СН лежит против угла в 30°, поэтому он равен половине гипотенузы СМ. Отсюда СМ = 2СН = 4 см, АВ = 2СМ = 8 см.

• Четырехугольник и его элементы
• Четырехугольники и окружность
• Параллелограмм, его свойства и признаки
• Площадь параллелограмма
• Соотношения в прямоугольном треугольнике
• Сумма углов треугольника
• Внешний угол треугольника
• Свойство точек биссектрисы угла

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Урок 22. Свойство катета прямоугольного треугольника, лежащего против угла в 30° (7 класс)Скачать

Треугольник. Свойство прямоугольного треугольника с углом в 30°.

Катет прямоугольного треугольника, противолежащий углу в 30°, будет равняться половине гипотенузы.

Изобразим прямоугольный треугольник АСВ с углом В = 30°. В этом случае второй его острый угол будет 60°.

Обоснуем, что катет АС равняется половине гипотенузы АВ то есть АС = 1/2АВ.

Продлим катет АС за вершину прямого угла С и начертим отрезок СМ, причем части равные СМ=АС. Прочертим ВМ, соединив таким образом точки В и М. Сформированные прямоугольные треугольники ВСМ и АСВ эквиваленты (равны по двум катетам). Наглядно видно, что всякий угол треугольника АМВ по 60°, значит можно сделать вывод, что образовавшийся треугольник — равносторонний.

Сторона АС = 1/2 АМ, а поскольку АМ = АВ, а значит и катет АС будет равен 1/2 гипотенузы АВ.

🎦 Видео

Свойства прямоугольного треугольника. 7 класс.Скачать

Задача о катете треугольника 30, 60, 90Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Задачи на правило 30 грдаусов в прямоугольном треугольнике и немного теорема пифагораСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Теорема Пифагора для чайников)))Скачать

№485. Найдите катет прямоугольного треугольника, лежащий против угла 60°, если гипотенуза равна с.Скачать

Урок 1. Почему катет, лежащий напротив 30 градусов равен половине гипотенузы? №15 ОГЭ.Скачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Известна площадь прямоугольного треугольника и один из острых углов. Найти противолежащий катетСкачать

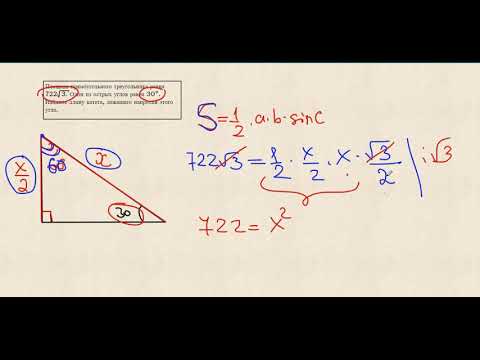
Катет напротив 30° равен половине гипотенузыСкачать

Свойство прямоугольного треугольникаСкачать

Некоторые свойства прямоугольного треугольника | Геометрия 7-9 класс #35 | ИнфоурокСкачать

Угол 30 градусов в прямоугольном треугольникеСкачать

Свойства прямоугольного треугольникаСкачать

Катет, лежащий напротив угла в 30 градусовСкачать