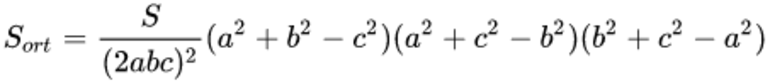Теорема пересечения высот треугольника (6 видео)

Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра

Содержание

Что такое высота
Свойства ортоцентра
Полезные факты
Задача Фаньяно
История изучения
Теорема о пересечении высот треугольника
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
📽️ Видео

Видео:8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать

Что такое высота

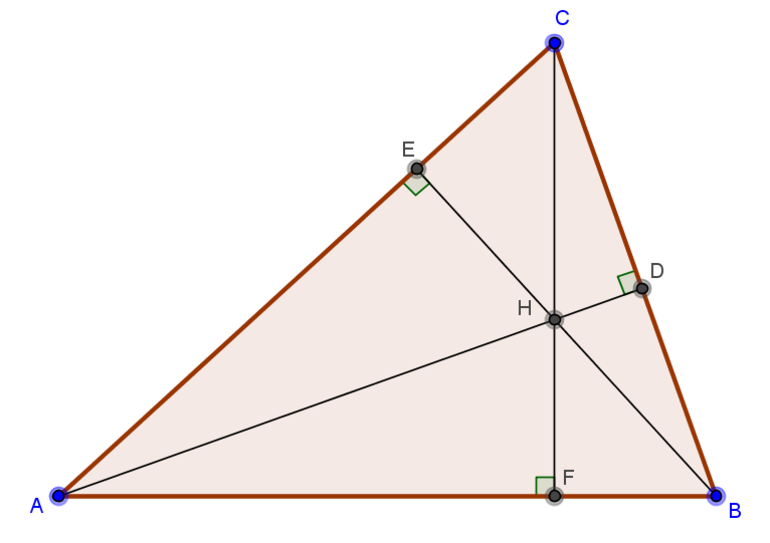
Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

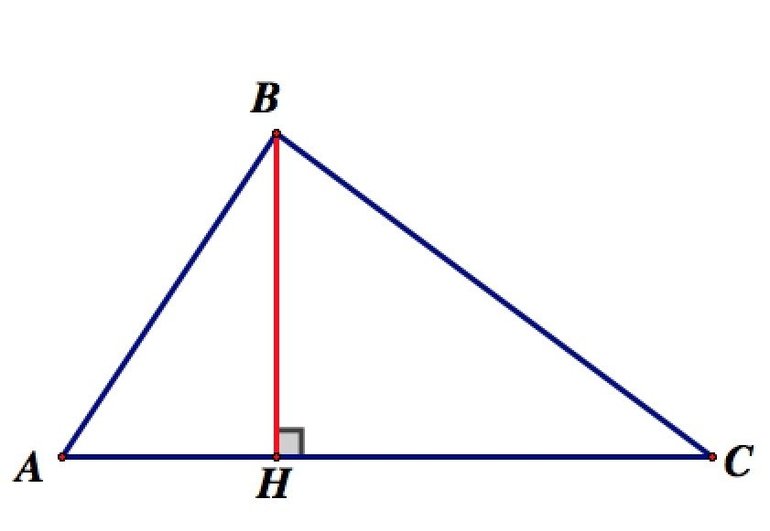
У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Видео:Геометрия 8 класс (Урок№31 - Теорема о пересечении высот треугольника.)Скачать

Свойства ортоцентра

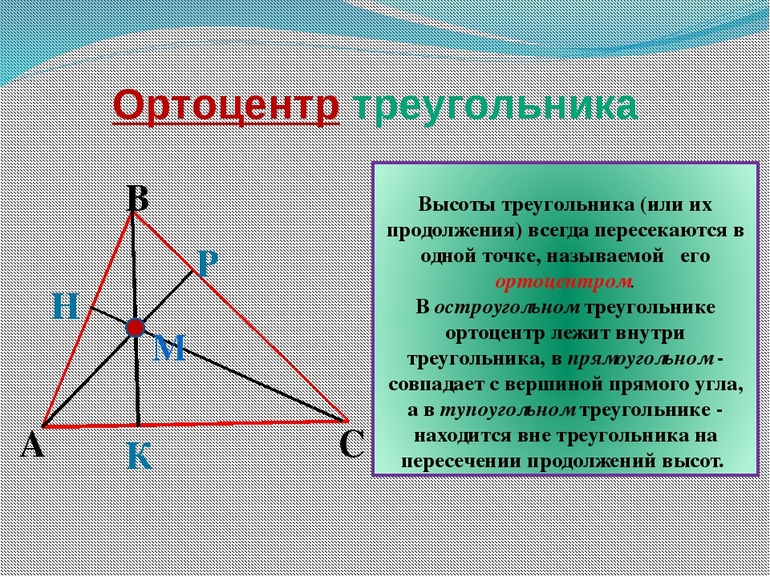
Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

внутри;
снаружи;
в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

H — ортоцентр в ABC;
О — центр описанной окружности.

Тогда:

окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
отрезок BH вдвое длиннее отрезка АС;
середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

Видео:ПЕРЕСЕЧЕНИЕ ВЫСОТ треугольника ТЕОРЕМА 8 класс АтанасянСкачать

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

Видео:72 Теорема о пересечении высот треугольникаСкачать

Теорема о пересечении высот треугольника

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим важную теорему о том, что высоты треугольника или их продолжения пересекаются в одной точке.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»

Видео:Теорема о пересечении высот треугольникаСкачать

Please wait.

Видео:76. Теорема о пересечении высот треугольникаСкачать

We are checking your browser. mathvox.ru

Видео:Теорема о пересечении высот треугольника | Геометрия 7-9 класс #73 | ИнфоурокСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Новое доказательство пересечения высот треугольника в одной точкеСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d7c269b082f16f0 • Your IP : 85.95.188.35 • Performance & security by Cloudflare