Видео:Свойство пересекающихся хорд окружности. Геометрия 8-9 классСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Задачи по геометрии 8 класс. Касательные, отрезки пересекающихся хорд и отрезки секущих к окружности.
Свойство пересекающихся хорд: произведение
отрезков одной хорды равно произведению
отрезков другой хорды
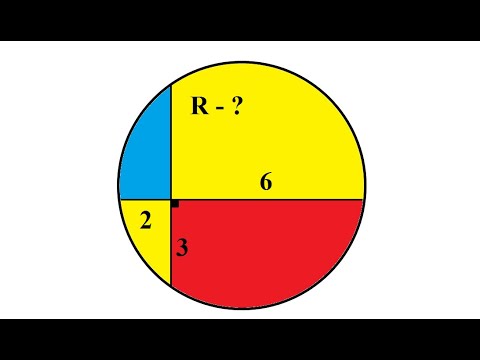
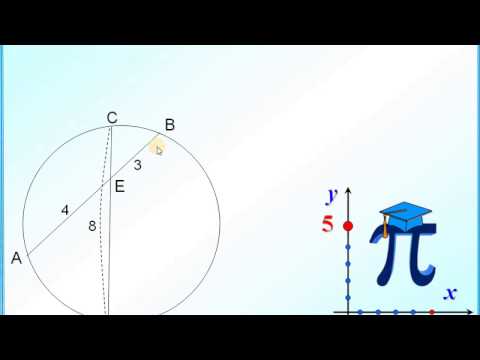
Хорды окружности АВ и СР пересекаются в точке Е. Найти длину отрезка РЕ, если СЕ= 8см, АЕ = 3 см, ВЕ = 6 см.
Хорды окружности АК и МЕ пересекаются в точке О. Найти длину отрезка МО, если АО= 4см, ОЕ = 5 см, ОК = 15 см.
Хорды окружности АК и МЕ пересекаются в точке О. Найти длину отрезка МО и ОЕ, если АО = 2 см, ОК = 12 см, МЕ = 10 см.
Хорды окружности АВ и СР пересекаются в точке Е. Найти длину отрезка РЕ и СЕ, если СР = 12 см, АЕ=7 см, ЕВ = 4 см.
Хорды окружности АВ и СД пересекаются в точке О. Найти длину отрезка ДО и ОС, если АО = 12 см, ОВ=4 см, ДО : ОС = 3 : 4.
Хорды окружности МК и СД пересекаются в точке А. Найти длину отрезка ДО и ОС, если МА = 6 см, АК=15 см, СА : АД = 2 : 5.
Свойство секущих к окружности, исходящих из
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АС и ВС, если АМ = 3, МК = 5, АВ = 4.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и МК, если АВ = 4, ВС = 6, АК = 12.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и АС, если АМ = 2, АК = 6, длина отрезка АС на 4 больше длины отрезка АВ.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и АК, если АВ = 2, АС = 8, длина отрезка АМ на 6 меньше длины отрезка АК.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и ВС, если АМ = 4, АК = 6, АВ : ВС = 2 :4.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и АК, если АМ : АК = 3 : 5, АВ = 5, ВС = 7.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и АС, если АМ = 2, АК = 4, длина отрезка ВС на 6 больше длины отрезка АВ.
Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и МК, если АМ на 8 меньше длины отрезка МК и длина отрезка АВ = 3, АС = 8.
Свойство секущей и касательной к окружности,
исходящих из одной точки:
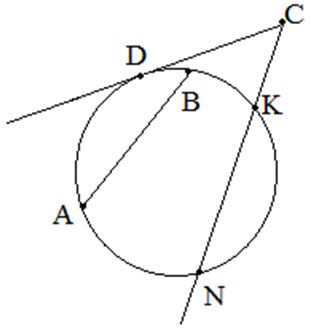
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АВ, если АК = 4, АР = 9.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АВ, если АК = 4, АР = 16.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР, если АК = 4, АВ = 8.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР, если АК = 5, АВ = 10.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АК и АР, если АВ = 5, а отрезок КР на 5 больше отрезка АК.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АК и АР, если АВ = 6, а отрезок КР на 6 больше отрезка АК.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР и АК, если АК : КР = 4 : 5, АВ = 12.
Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР и АК, если АК : КР = 1 : 3, АВ = 14.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Окружность. Свойства отрезков пересекающихся хорд, секущих и касательных
Презентация к уроку
Цель: повысить мотивацию к обучению; развивать вычислительные навыки, сообразительность, умение работать в команде.
Окружность — это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.
На слайде изображена окружность, отмечен ее центр — точка О, проведены два отрезка: ОА и СВ. Отрезок ОА соединяет центр окружности с точкой на окружности. Он называется РАДИУСОМ (по-латыни radius — “спица в колесе”). Отрезок СВ соединяет две точки окружности и проходит через ее центр. Это диаметр окружности (в переводе с греческого – “поперечник”).
Также нам понадобится определение хорды окружности — это отрезок, соединяющий две точки окружности (на рисунке – хорда DE).
Давайте выясним вопрос о взаимном расположении прямой и окружности.
Следующий вопрос и он будет основным: выяснить свойства, которыми обладают пересекающиеся хорды, секущие и касательные.
Доказывать эти свойства вы будете на уроках математики, а наша задача научиться применять эти свойства при решении задач, так как они находят широкое применение на экзаменах и в форме ЕГЭ, и в форме ГИА.
Задание для команд.
Далее продолжим работать в парах над решением простейших задач по применению этих свойств:
Используя данные на рисунке, найдите х. Слайд 5–6
Кто быстрее, правильней. С последующим обсуждением и проверкой решения всех задач. Отвечающие зарабатывают для своей команды поощрительные баллы.
Ну, а теперь приступим к решению более серьезных задач. Вашему вниманию предлагается три блока: пересекающиеся хорды, касательная и секущая, две секущие. Подробным образом разберем решение по одной задачи из каждого блока.
(Разбирается решение с подробной записью №4, №7, №12)
2. Практикум по решению задач
а) Пересекающиеся хорды
1. E – точка пересечения хорд AB и CD. AE=4, AB=10, СE:ED=1:6. Найти CD.
Решение:
2. E – точка пересечения хорд AB и CD. AB=17, CD=18, ED=2CE. Найти AE и BE.
Решение:
3. E – точка пересечения хорд AB и CD. AB=10, CD=11, BE=CE+1. Найти CE.
Решение:
4. E – точка пересечения хорд AB и CD. ED=2AE, CE=DE-1, BE=10. Найти CD.
Решение:
б) Касательная и секущая
5. Из одной точки проведены к окружности касательная и секущая. Касательная равна 6, секущая – 18. Определить внутренний отрезок секущей.
Решение:
6. Из одной точки проведены к окружности касательная и секущая. Найти касательную, если известно, что она меньше внутреннего отрезка секущей на 4 и больше внешнего отрезка на 4.
Решение:
7. Из одной точки проведены к окружности касательная и секущая. Найти секущую, если известно, что внутренний её отрезок относится к внешнему, как 3:1, а длина касательной равна 12.
Решение:
8. Из одной точки проведены к окружности касательная и секущая. Найти внешний отрезок, секущей, если известно, что внутренний её отрезок 12, а длина касательной 8.
Решение:
9. Касательная и секущая, исходящие из одной точки, соответственно равны 12 и 24. Определить радиус окружности, если секущая удалена от центра на 12.
Решение:
10. Из одной точки проведены к окружности две секущие, внутренние отрезки которых соответственно равны 8 и 16. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой. Найти длину каждой секущей.
Решение:
11. Из одной точки проведены к окружности две секущие. Внешний отрезок первой секущей относится к своему внутреннему, как 1:3. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой и относится к своему внутреннему отрезку, как 1:8. Найти длину каждой секущей.
Решение:
12. Через точку А, которая находится вне окружности на расстоянии 7 от её центра, проведен прямая, пересекающая окружность в точках В и С. Найдите длину радиуса окружности, если АВ=3, ВС=5.
Решение:
13. Из точки А проведены к окружности секущая длиной 12 см и касательная, составляющая 
Решение:
3. Закрепление знаний
Считаю, что вы обладаете достаточным запасом знаний, чтобы отправится в небольшое путешествие по лабиринтам вашего интеллекта, посетив следующие станции:
- Соображай-ка!
- Решай-ка!
- Отвечай-ка!
На станции можно находиться не более 6 минут. За каждое верное решение задачи команда получает поощрительные баллы.
Командам вручаются маршрутные листы:
| Станция | Номера задач | Отметка о решении |
| Решай-ка! | №1, №3 | |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
4. Подведение итогов
Хотелось бы подвести итоги нашего занятия:
Помимо новых знаний надеюсь, вы лучше познакомились друг с другом, приобрели опыт работы в команде. А как вы думаете, полученные знания находят где-то применение в жизни?
Поэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в своем романе “Каванг”, позволяют запечатлеть на всю жизнь некоторые теоремы и их применение. Читаем в романе следующую задачу:
“Лилия, на одну пядь поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в двух локтях от прежнего места; исходя из этого требовалось определить глубину озера” (1 пядь равна 10 дюймам, 2 локтя – 21 дюйму).
А решается эта задача на основе свойства пересекающихся хорд. Посмотрите на рисунок, и станет ясно, как находится глубина озера.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика. Задачи. Хорды, касательные и секущие.
Хорды, касательные и секущие.
Окружностью называется геометрическое место точек, равноудаленных от одной точки, которая называется центром окружности.
Отрезок, соединяющий две точки окружности, называется хордой (на рисунке это отрезок ). Хорда, проходящая через центр окружности, называется диаметром окружности.
Хорда окружности обладает следующими свойствами:
- Хорды, находящиеся на одинаковом расстоянии от центра окружности, равны.
- Если хорды стягивают равные центральные углы, то они равны.
- Если диаметр перпендикулярен хорде, то он проходит через ее середину.
- Если вписанные углы опираются на одну хорду, то они равны.
- Две дуги равны, если они заключены между двумя равными хордами.
- Если пара вписанных углов опирается на одну и ту же хорду, а их вершины лежат по разные стороны хорды, то их сумма составляет 180°.
- Для любых двух хорд
и
, пересекающихся в точке О, выполняется равенство:
.
Прямая, имеющая с окружностью одну общую точку, называется касательной (на рисунке отрезок ).
Прямая, имеющая с окружностью две общие точки, называется секущей (отрезок ).
Свойства касательной и секущей
- Касательная перпендикулярна радиусу, проведенному в точку касания.
- Отрезки касательных, проведенных из одной точки, равны.
- Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть:
🎦 Видео
Теорема об отрезках хорд и секущихСкачать

Пересекающиеся хорды окружности. Решишь задачу?Скачать

Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать

Свойство хорд, пересекающихся внутри окружностиСкачать
Теорема о произведении отрезков пересекающихся хорд.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

теоренма об отрезках пересекающихся хордСкачать

Докажите, что произведение отрезков одной хорды равно произведению отрезков другой хордыСкачать

Свойство диаметра окружности. 7 класс.Скачать

№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Свойства хорд, касательных, секущих окружности I Для решения задач из ОГЭ И ЕГЭ I Часть 1Скачать

Задание 24 Свойство пересекающихся хордСкачать

теорема об отрезках пересекающихся хорд и еще несколько свойств окружностиСкачать

Математика ОГЭ Задание 24 Отрезки пересекающихся хордСкачать
Окружность. 7 класс.Скачать

Теорема о секущей и касательной, о секущих, о пересекающихся хордах | Теоремы об окружностях - 1Скачать

Найти радиус окружности если известны длины пересекающихся хордСкачать