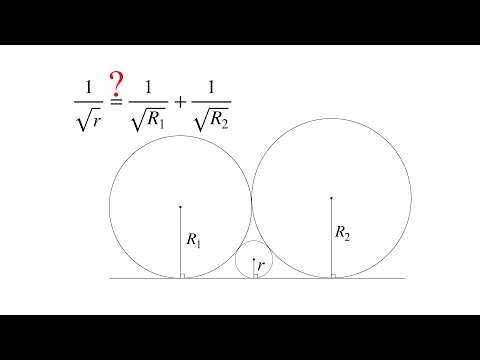
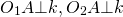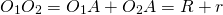Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним.
- Внутреннее касание
- Внешнее касание
- Касание двух окружностей
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- 🎬 Видео
Видео:КАСАЮЩИЕСЯ ОКРУЖНОСТИСкачать
Внутреннее касание
Касание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом.
При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов.
Видео:ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать
Внешнее касание
Касание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом.
При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов.
Видео:Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать
Касание двух окружностей
Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.
Общая точка двух окружностей называется точкой касания окружностей.
Касание окружностей может быть внешним и внутренним.
Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной.
Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.
Касающиеся окружности имеют только одну общую точку — точку касания.
Центры касающихся окружностей и их общая точка касания лежат на одной прямой.
При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания:
По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k.
Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой.
Что и требовалось доказать .
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами окружностей равно разности радиусов:
Видео:Касание окружностейСкачать
Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:ЕГЭ Задание 16 Три окружностиСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:ПЛАНИМЕТРИЯ ЕГЭ | 16 задача из 1 варианта Ященко 2021 🔴Скачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, 🎬 ВидеоЕГЭ Задание 16 Внутреннее касание двух окружностейСкачать  КРАСИВАЯ ПЛАНИМЕТРИЧЕСКАЯ ЗАДАЧА (3 ОКРУЖНОСТИ)Скачать  7 класс, 21 урок, ОкружностьСкачать  ОГЭ № 25. "Окружности касаются внешним образом... "Скачать  Круг. Окружность | Математика 3 класс #21 | ИнфоурокСкачать  Окружности соприкасаются внутренним образом.#hard (1 вариант решения)Скачать  9 класс, 8 урок, Взаимное расположение двух окружностейСкачать  ✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Задание 18 все типы | МАТЕМАТИКА ОГЭ 2023Скачать  Задача №16. Пересекающиеся и касающиеся окружности.Скачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать  |
