Сумма углов прямоугольного треугольника (8 видео)

Сумма углов прямоугольного треугольника

Средняя оценка: 4.5

Всего получено оценок: 164.

Средняя оценка: 4.5

Всего получено оценок: 164.

Сумма углов любого треугольника – величина устойчивая. Но прямоугольный треугольник выделяется среди прочих набором специфических свойств. Сумма углов не является исключением, поэтому стоит поговорить об этом свойстве прямоугольных треугольников, чтобы не возникало вопросов в дальнейшем изучении.

Содержание

Треугольник
Сумма углов треугольника
Прямоугольный треугольник
Что мы узнали?
Сумма углов прямоугольного треугольника – чему равна
Треугольник
Сумма углов треугольника
Прямоугольный треугольник
Что мы узнали?
Геометрия. 7 класс
📺 Видео

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Треугольник

Несмотря на свою обособленность от прочих фигур, треугольник является таким же многоугольником, как и прямоугольник, квадрат или ромб. Все отличие только в количестве углов. Существует формула, по которой определяется сумма углов любого многоугольника в зависимости от количества сторон, поговорим о ней немного позже.

Итак, треугольник это фигура, имеющая три стороны и три угла. Традиционно, одна из сторон считается основанием, а две другие стороны зовутся боковыми. Обозначение не является принципиальным, поэтому любая из сторон треугольника принимается за условное основание. Такое обозначение нужно только для облегчения понимания чертежа.

Треугольник в математике считается минимально возможно фигурой. Любая из возможных фигур может быть разбита на треугольники. Это свойство иногда используется при решении задач.

Видео:№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

Сумма углов треугольника

Есть два варианта нахождения общей суммы углов треугольника:

Математический анализ. За столь страшными словами кроется обычная простая формула:

180*(n-2)- где n – количество сторон многоугольника.

Второй способ – геометрический. Именно таким образом было в первый раз выведено утверждение о том, что сумма углов треугольника равна 180 градусам. Рассмотрим его подробнее.

Рис. 2. Рисунок к задаче

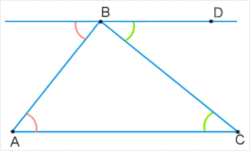
Пусть треугольник АВС – произвольный треугольник с основанием АС. Тогда построим прямую ВD, проходящую через точку В, параллельно основанию. Тогда получается две параллельные прямые: АС и ВD с двумя секущими АВ и ВС.

Рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.

Важно понимать, что наружные углы нельзя называть внешними углами треугольника, так как внешние углы получаются с помощью продолжения одной из сторон треугольника, а прямая ВD продолжением стороны треугольника не является.

Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.

Видео:Сумма острых углов прямоугольного треугольника равна 90°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Прямоугольный треугольник

Прямоугольный треугольник содержит угол в 90 градусов. Такой угол зовут прямым, отсюда и название фигуры. Чему равна сумма углов прямоугольного треугольника? Так же,как и в любом другом треугольнике – 180 градусам. Но если один из углов определен и равен 90 градусам, то можно определить сумму двух оставшихся:

180-90=90 – то есть сумма непрямых углов прямоугольного треугольника равна 90 градусам.

Но непрямые углы это нематематическое определение. Может ли в прямоугольном треугольнике еще один угол быть прямым? Если бы такой угол мог существовать, то он был бы равен 90 градусам. То есть оставшийся третий угол:

90-90=0 – и третий угол в этом случае был бы нулевым, что невозможно. Так же, как и невозможно существование тупого угла в прямоугольном треугольнике. Потому что тупой угол всегда больше 90 градусов.

Значит, можно сделать вывод о том, что в прямоугольном треугольнике сумма острых углов равна 90 градусам.

Рис. 3. Острые углы прямоугольного треугольника

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Что мы узнали?

Мы поговорили о формуле суммы углов прямоугольного треугольника. Вывели ее геометрическим способом и определили аналитический способ вывода, который вытекает из геометрического. Рассказали, почему невозможно существование тупоугольного прямоугольного треугольника.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Сумма углов прямоугольного треугольника – чему равна

Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Треугольник

Треугольник в математике считается минимально возможно фигурой. Любая из возможных фигур может быть разбита на треугольники. Это свойство иногда используется при решении задач.

Рис. 1. Фигура, разбитая на треугольники

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Сумма углов треугольника

Есть два варианта нахождения общей суммы углов треугольника:

Математический анализ. За столь страшными словами кроется обычная простая формула:

180*(n-2)- где n – количество сторон многоугольника.

Второй способ – геометрический. Именно таким образом было в первый раз выведено утверждение о том, что сумма углов треугольника равняется 180 градусам. Рассмотрим его подробнее.

Рис. 2. Рисунок к задаче

Тогда рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.

Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.

Видео:Сумма углов прямоугольного треугольника равна 90°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Прямоугольный треугольник

Прямоугольный треугольник содержит угол в 90 градусов. Такой угол зовут прямым, отсюда и название фигуры. Чему равна сумма углов прямоугольного треугольника? Так же, в любом другом треугольнике 180 градусов. Но если один из углов определен и равен 90 градусам, то можно определить сумму двух оставшихся:

180-90=90 – то есть сумма непрямых углов прямоугольного треугольника равняется 90 градусам.

90-90=0 – то есть третий угол в этом случае был бы нулевым, что невозможно. Так же, как и невозможно существование тупого угла в прямоугольном треугольнике. Потому что тупой угол всегда больше 90 градусов.

Значит, можно сделать вывод о том, что в прямоугольном треугольнике сумма острых углов равняется 90 градусам.

Рис. 3. Острые углы прямоугольного треугольника

Видео:Сумма острых углов прямоугольного треугольникаСкачать

Что мы узнали?

Видео:Сумма углов треугольникаСкачать

Геометрия. 7 класс

Конспект урока

Сумма углов треугольника

Перечень рассматриваемых вопросов:

Формулирование и доказательство теоремы о сумме углов треугольника.
Следствия теоремы о сумме углов треугольника.
Классификация треугольников по видам углов.
Формулирование и доказательство теоремы о свойствах прямоугольного треугольника.
Решение задач с применением пройденного материала;
Угловой отражатель.

Внешний угол треугольника– это угол, смежный с каким-либо углом этого треугольника.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее, на уроках математики, вы познакомились с различными геометрическими фигурами, в том числе и с треугольниками. При изучении геометрии, вы узнали признаки равенства треугольников, выяснили, что такое медиана, биссектриса и высота треугольника.

Сегодня мы продолжим изучать треугольники и рассмотрим одну из важнейших теорем геометрии– теорему о сумме углов треугольника.

Сформулируем эту теорему.

Сумма углов треугольника равна 180°.

Проведем через вершину В прямую а ║АС.

∠1 = ∠4 (по свойству параллельных прямых, т. к. это накрест лежащие углы при пересечении прямых а и АС и секущей АВ), ∠3 = ∠5 (по свойству параллельных прямых, т. к. это – накрест лежащие углы при пересечении прямых а и АС и секущей ВС)→ ∠4 + ∠2 + ∠5 = 180° (по свойству развёрнутого угла) → ∠1 + ∠2 + ∠3 = 180° → ∠А + ∠В + ∠С = 180°.

Что и требовалось доказать.

Теперь введём ещё одно понятие, связанное с треугольниками –внешний угол треугольника. Это угол, смежный с каким-либо углом этого треугольника.

Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

∠3 + ∠4 = 180° (по свойству развёрнутого угла).

∠3 + (∠2 + ∠1) = 180° (по теореме о сумме углов треугольника) → ∠4 = ∠2 + ∠1.

Что и требовалось доказать.

Из теоремы о сумме углов треугольника следует, что если один из углов треугольника равен 90 градусам или больше 90 градусов, то остальные два угла будут острые, т.к. их сумма не должна превышать 90 градусов. Поэтому, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

Исходя из этого, можно классифицировать треугольники по углам.

По углам треугольник может быть:

‑ остроугольным, если все его углы являются острыми (т.е. меньше 90°);

‑ тупоугольным, если один из его углов тупой (т.е. больше 90°);

‑ прямоугольным, если один угол 90° (т.е. прямой).

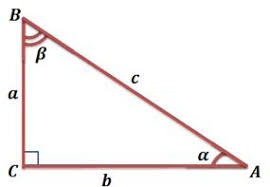
В прямоугольном треугольнике стороны имеют свои названия.

Сторона треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие – катетами.

Докажем свойство прямоугольного треугольника, которое устанавливается с помощью теоремы о сумме углов треугольника.

Сумма двух острых углов прямоугольного треугольника равна 90º.

∠А +∠С + ∠В = 180° (по теореме о сумме углов треугольника).

∠В = 90° (по определению прямоугольного треугольника) →∠А + ∠С + 90° = 180°

∠А + ∠С = 180 – 90° = 90°

Что и требовалось доказать.

Докажем, что в равностороннем треугольнике каждый угол равен 60 °.

Доказать: ∠А =∠С = ∠В = 60°.

Так как треугольник АВС равносторонний →АС = АВ = ВС (по определению равностороннего треугольника) → если АС = АВ → ∠С = ∠В (по свойству равнобедренного треугольника). Аналогично, если АС = СВ → ∠А = ∠В (по свойству равнобедренного треугольника) → ∠А = ∠С = ∠В.

∠А + ∠С + ∠В = 180° (по теореме о сумме углов треугольника).

∠А = ∠С = ∠В = 180° : 3 = 60°.

Что и требовалось доказать.

Материал для углублённого изучения темы.

Одно из свойств прямоугольного треугольника ‑сумма двух его острых углов равна 90°‑используется в технике, например, в угловом отражателе. Это устройство, которое отражает падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей.

Отражатель, например, устанавливается на заднем крыле велосипеда, для того, чтобы «возвращать назад» свет автомобильных фар, чтобы водитель машины видел велосипедиста ночью.

Ещё угловой отражаетель был установлен на автоматической космической станции, запущенной на Луну( выделен на рисунке кружочком), с целью определения точного расстояния от Земли до Луны.