Сумма градусов прямоугольного треугольника

Средняя оценка: 4.5

Всего получено оценок: 165.

Средняя оценка: 4.5

Всего получено оценок: 165.

Сумма углов любого треугольника – величина устойчивая. Но прямоугольный треугольник выделяется среди прочих набором специфических свойств. Сумма углов не является исключением, поэтому стоит поговорить об этом свойстве прямоугольных треугольников, чтобы не возникало вопросов в дальнейшем изучении.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Треугольник

Несмотря на свою обособленность от прочих фигур, треугольник является таким же многоугольником, как и прямоугольник, квадрат или ромб. Все отличие только в количестве углов. Существует формула, по которой определяется сумма углов любого многоугольника в зависимости от количества сторон, поговорим о ней немного позже.

Итак, треугольник это фигура, имеющая три стороны и три угла. Традиционно, одна из сторон считается основанием, а две другие стороны зовутся боковыми. Обозначение не является принципиальным, поэтому любая из сторон треугольника принимается за условное основание. Такое обозначение нужно только для облегчения понимания чертежа.

Треугольник в математике считается минимально возможно фигурой. Любая из возможных фигур может быть разбита на треугольники. Это свойство иногда используется при решении задач.

Видео:Сумма острых углов прямоугольного треугольника равна 90°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Сумма углов треугольника

Есть два варианта нахождения общей суммы углов треугольника:

• Математический анализ. За столь страшными словами кроется обычная простая формула:

180*(n-2)- где n – количество сторон многоугольника.

• Второй способ – геометрический. Именно таким образом было в первый раз выведено утверждение о том, что сумма углов треугольника равна 180 градусам. Рассмотрим его подробнее.

Рис. 2. Рисунок к задаче

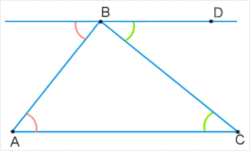
Пусть треугольник АВС – произвольный треугольник с основанием АС. Тогда построим прямую ВD, проходящую через точку В, параллельно основанию. Тогда получается две параллельные прямые: АС и ВD с двумя секущими АВ и ВС.

Рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.

Важно понимать, что наружные углы нельзя называть внешними углами треугольника, так как внешние углы получаются с помощью продолжения одной из сторон треугольника, а прямая ВD продолжением стороны треугольника не является.

Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.

Видео:№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

Прямоугольный треугольник

Прямоугольный треугольник содержит угол в 90 градусов. Такой угол зовут прямым, отсюда и название фигуры. Чему равна сумма углов прямоугольного треугольника? Так же,как и в любом другом треугольнике – 180 градусам. Но если один из углов определен и равен 90 градусам, то можно определить сумму двух оставшихся:

180-90=90 – то есть сумма непрямых углов прямоугольного треугольника равна 90 градусам.

Но непрямые углы это нематематическое определение. Может ли в прямоугольном треугольнике еще один угол быть прямым? Если бы такой угол мог существовать, то он был бы равен 90 градусам. То есть оставшийся третий угол:

90-90=0 – и третий угол в этом случае был бы нулевым, что невозможно. Так же, как и невозможно существование тупого угла в прямоугольном треугольнике. Потому что тупой угол всегда больше 90 градусов.

Значит, можно сделать вывод о том, что в прямоугольном треугольнике сумма острых углов равна 90 градусам.

Рис. 3. Острые углы прямоугольного треугольника

Видео:Найдите площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать

Что мы узнали?

Мы поговорили о формуле суммы углов прямоугольного треугольника. Вывели ее геометрическим способом и определили аналитический способ вывода, который вытекает из геометрического. Рассказали, почему невозможно существование тупоугольного прямоугольного треугольника.

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Сумма углов прямоугольного треугольника – чему равна

Сумма углов любого треугольника – величина устойчивая. Но прямоугольный треугольник выделяется среди прочих набором специфических свойств. Сумма углов не является исключением, поэтому стоит поговорить об этом свойстве прямоугольных треугольников, чтобы не возникало вопросов в дальнейшем изучении.

Видео:Сумма острых углов прямоугольного треугольникаСкачать

Треугольник

Несмотря на свою обособленность от прочих фигур, треугольник является таким же многоугольником, как и прямоугольник, квадрат или ромб. Все отличие только в количестве углов. Существует формула, по которой определяется сумма углов любого многоугольника в зависимости от количества сторон, поговорим о ней немного позже.

Итак, треугольник это фигура, имеющая три стороны и три угла. Традиционно, одна из сторон считается основанием, а две другие стороны зовутся боковыми. Обозначение не является принципиальным, поэтому любая из сторон треугольника принимается за условное основание. Такое обозначение нужно только для облегчения понимания чертежа.

Треугольник в математике считается минимально возможно фигурой. Любая из возможных фигур может быть разбита на треугольники. Это свойство иногда используется при решении задач.

Рис. 1. Фигура, разбитая на треугольники

Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Сумма углов треугольника

Есть два варианта нахождения общей суммы углов треугольника:

• Математический анализ. За столь страшными словами кроется обычная простая формула:

180*(n-2)- где n – количество сторон многоугольника.

• Второй способ – геометрический. Именно таким образом было в первый раз выведено утверждение о том, что сумма углов треугольника равняется 180 градусам. Рассмотрим его подробнее.

Рис. 2. Рисунок к задаче

Пусть треугольник АВС – произвольный треугольник с основанием АС. Тогда построим прямую ВD, проходящую через точку В, параллельно основанию. Тогда получается две параллельные прямые: АС и ВD с двумя секущими АВ и ВС.

Тогда рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.

Важно понимать, что наружные углы нельзя называть внешними углами треугольника, так как внешние углы получаются с помощью продолжения одной из сторон треугольника, а прямая ВD продолжением стороны треугольника не является.

Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.

Видео:Теорема Пифагора для чайников)))Скачать

Прямоугольный треугольник

Прямоугольный треугольник содержит угол в 90 градусов. Такой угол зовут прямым, отсюда и название фигуры. Чему равна сумма углов прямоугольного треугольника? Так же, в любом другом треугольнике 180 градусов. Но если один из углов определен и равен 90 градусам, то можно определить сумму двух оставшихся:

180-90=90 – то есть сумма непрямых углов прямоугольного треугольника равняется 90 градусам.

Но непрямые углы это нематематическое определение. Может ли в прямоугольном треугольнике еще один угол быть прямым? Если бы такой угол мог существовать, то он был бы равен 90 градусам. То есть оставшийся третий угол:

90-90=0 – то есть третий угол в этом случае был бы нулевым, что невозможно. Так же, как и невозможно существование тупого угла в прямоугольном треугольнике. Потому что тупой угол всегда больше 90 градусов.

Значит, можно сделать вывод о том, что в прямоугольном треугольнике сумма острых углов равняется 90 градусам.

Рис. 3. Острые углы прямоугольного треугольника

Видео:7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Что мы узнали?

Мы поговорили о формуле суммы углов прямоугольного треугольника. Вывели ее геометрическим способом и определили аналитический способ вывода, который вытекает из геометрического. Рассказали, почему невозможно существование тупоугольного прямоугольного треугольника.

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Углы прямоугольного треугольника

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Калькулятор расчёта углов прямоугольного треугольника

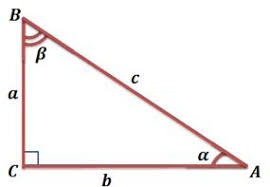
Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

• tg α — тангенс угла α
• a — противолежащий катет
• b — прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Видео:Сумма углов прямоугольного треугольника равна 90°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла — острые.

📺 Видео

Решение задач (сумма острых углов прямоугольного треугольника)Скачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Почему сумма углов треугольника 180 градусов?Скачать

Нахождение стороны прямоугольного треугольникаСкачать

Решение прямоугольных треугольниковСкачать

1698 один из острых углов прямоугольного треугольника равен 57 градусовСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать