Сторона правильного шестиугольника вписанного в окружность равна 8см

Правильный шестиугольник – это геометрическая фигура; правильный многоугольник с 6 равными углами и сторонами.

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Общая формула вычисления площади

Площадь (S) правильного шестиугольника вычисляется по формуле ниже, где a – длина его стороны:

Формула получена следующим образом:

Правильный шестиугольник состоит из шести равных равносторонних треугольников. Площадь каждого рассчитывается так:

Следовательно, площадь правильного шестиугольника равна:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Площадь правильного шестиугольника, вписанного в окружность

Сторона правильного шестиугольника равняется радиусу окружности, описанной вокруг него (a=r).

Это значит, что формула площади может быть представлена в таком виде (а заменяем на r):

Видео:ЕГЭ-2014 Задание В-8 Урок №185 Чему равна сторона правильного шестиугольника...Скачать

Примеры задач

Задание 1
Сторона правильного шестиугольника равна 8 см. Найдите его площадь.

Решение:
Используем первую формулу, в которой задействована длина стороны:

Задание 2
Вычислите площадь правильного шестиугольника, ели радиус описанной вокруг нее окружности равен 15 см.

Решение:
Воспользуемся второй формулой (через радиус окружности):

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

ГДЗ по геометрии 9 класс Мерзляк дидактические материалы контрольная работа вариант №2 — 2

Авторы: Мерзляк А.Г. , Полонский В.Б. , Рабинович Е.М. , Якир М.С. .

Издательства: Просвещение, Вентана-граф 2017-2021

Тип: Дидактические материалы, Алгоритм успеха

Подробный решебник (ГДЗ) по Геометрии за 9 (девятый) класс дидактические материалы — готовый ответ контрольная работа вариант №2 — 2. Авторы учебника: Мерзляк, Полонский, Рабинович, Якир. Издательство: Вентана-граф 2017-2021.

Видео:Геометрия - Построение шестиугольникаСкачать

Похожие ГДЗ

ГДЗ учебник геометрия 9 класс А.Г. Мерзляк

ГДЗ Самостоятельные и контрольные работы геометрия 9 класс Мерзляк А.Г. углубленный уровень

ГДЗ учебник геометрия 9 класс Мерзляк А.Г. углубленный уровень

ГДЗ Математические диктанты, Контрольные работы (Методическое пособие) геометрия 9 класс Буцко Е.В.

ГДЗ Рабочая тетрадь геометрия 9 класс Мерзляк А.Г.

1. Найдите углы правильного 72-угольника. 2. Найдите площадь круга, вписанного в правильный треугольник со стороной 6 см. 3. В окружность вписан правильный шестиугольник со стороной 4 см. Найдите сторону квадрата, описанного около этой окружности. 4. Радиус окружности, описанной около правильного многоугольника, равен 42 см, а сторона многоугольника — 8 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника. 5. Сторона треугольника равна 6√3 см, а прилежащие к ней углы равны 50° и 70°. Найдите длины дуг, на которые делят окружность, описанную около треугольника, его вершины. 6. Найдите диагональ AD правильного восьмиугольника ABCDEFKP, если АВ = а.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Шестиугольник, виды, свойства и формулы

Видео:Задача 6 №27917 ЕГЭ по математике. Урок 134Скачать

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Чем он отличается от неправильного?

Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.

В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.

В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.

Видео:Как построить шестиугольник вписанный в окружностьСкачать

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Видео:Как построить правильный шестиугольник.Скачать

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a1 = a2 = a3 = a4= a5= a6.

2. Все углы равны между собой и составляют 120°.

α1 = α2 = α3 = α4 = α5 = α6 = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

1. диаметр описанной окружности;
2. диаметр вписанной окружности;
3. площадь;
4. периметр.

Описанная окружность и возможность построения

Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

1. Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
2. Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
3. Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

1. Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
2. Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
3. Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
4. Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Видео:Вариант 32, №8. Радиус окружности, вписанной в правильный шестиугольник. Длина окружности. ЗадачаСкачать

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

Видео:Свойства правильного шестиугольника. Сравнение площадей. Разбор задачи из стереометрии.Скачать

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

Видео:Задание 24 Правильный шестиугольник вписан в окружностьСкачать

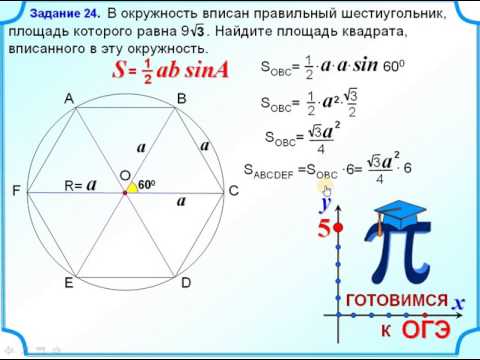
Правильный шестиугольник

Знаете ли вы, как выглядит правильный шестиугольник? Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.

Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.

Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?

Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.

Мы знаем, что площадь правильного треугольника: .

Тогда площадь правильного шестиугольника — в шесть раз больше.

, где — сторона правильного шестиугольника.

Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.

Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне. Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти. Он равен . Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.

Ты нашел то, что искал? Поделись с друзьями!

. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .

. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

(бесплатный звонок по России)
+7
(бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Обучающее видео БЕСПЛАТНО

Техническая поддержка: [email protected] (круглосуточно)

Закажите звонок и получите скидку -50% на первый месяц занятий!

Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.

📸 Видео

Длина окружности. Площадь круга - математика 6 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Построение правильного шестиугольника при помощи циркуля и линейкиСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

ЕГЭ Задание 16 Правильный шестиугольникСкачать

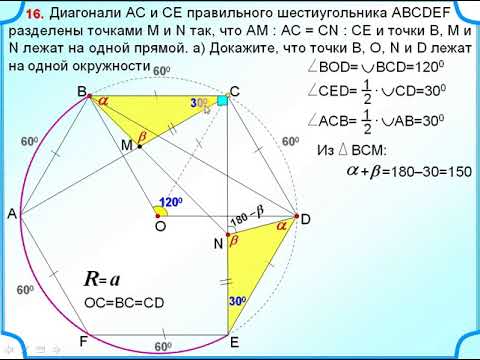
Построить описанную окружность (Задача 1)Скачать