Сторона квадрата равна 22 найдите радиус окружности вписанной в квадрат

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Округление:

Cторона, диаметр вписанной окружности (L) = 22

Диагональ, диаметр описанной окружности (M) = (sqrt<2*L^>) = (sqrt<2*22^>) = 31.11

Радиус вписанной окружности (R1) = (frac) = (frac) = 11

Радиус описанной окружности (R2) = (frac) = (frac) = 15.56

Периметр (P) = (L*4) = (22*4) = 88

Видео:СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:ПОДРОБНОЕ РЕШЕНИЕ ВОСЕМНАДЦАТОГО ЗАДАНИЯ ОГЭ МАТЕМАТИКА 2018Скачать

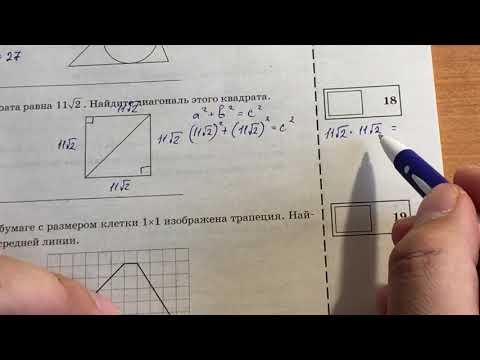
Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:ОГЭ ЗАДАНИЕ 15 НАЙДИТЕ РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ ОКОЛО КВАДРАТА #математика #2023 #огэ #mathСкачать

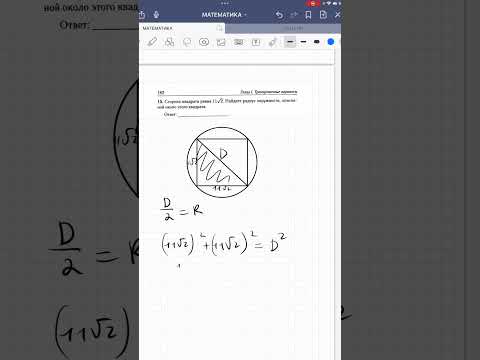
Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Задача № 27933 ЕГЭ по математике. Урок 147Скачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

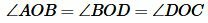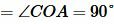(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

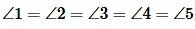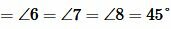(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Найдите сторону квадрата вписанного в окружность радиуса 22 корень из 2?

Геометрия | 5 — 9 классы

Найдите сторону квадрата вписанного в окружность радиуса 22 корень из 2.

Радиус описанной вокруг квадрата окружности равен половине диагонали квадрата, которая равна «a» квадратных корней из числа «2», где a — сторона квадрата, из чего следует, что радиус вышеназванной окружности равен»a» квадратных корней из числа «2», делённых на два

Приравняем две части «уравнения»

22 квадратных корня из двух = a квадратных корнейиз двух пополам

Умножаем обе части на два

44 квадратных корня из двух = a квадратных корней из двух

Делим обе части на квадратный корень из двух

Ответ : сторона квадрата равна 44.

Видео:17 задание ОГЭ по математикеСкачать

Найдите радиус окружности, вписанной в квадрат со стороной 12?

Найдите радиус окружности, вписанной в квадрат со стороной 12.

Видео:Задания 16. Тесты 1-5. ОГЭ. Математика.Скачать

Сторона квадрата равна 16см найдите радиусы вписанной и описанной окружности?

Сторона квадрата равна 16см найдите радиусы вписанной и описанной окружности.

Видео:17 задание из ОГЭСкачать

Правильный треугольник со стороной корень 12 вписан в окружность?

Правильный треугольник со стороной корень 12 вписан в окружность.

Найдите сторону квадрата вписанного в эту окружность.

Видео:Квадрат в окружности или окружность в квадрате #ShortsСкачать

Квадрат вписана окружность радиуса 2 см найдите сторону квадрата радиуса окружности описанной около данного квадрата?

Квадрат вписана окружность радиуса 2 см найдите сторону квадрата радиуса окружности описанной около данного квадрата.

Видео:Задание 16 Часть 3Скачать

В квадрат вписана окружность радиусом 2см?

В квадрат вписана окружность радиусом 2см.

Найти : сторону квадрата ; радиус окружности, описанный около данного квадрата.

Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Найдите сторону квадрата, вписанного в окружность радиуса 68 корней из 3?

Найдите сторону квадрата, вписанного в окружность радиуса 68 корней из 3.

Видео:R и r для квадрата. Как вывести формулы радиуса вписанной и описанной окружностей для квадрата.Скачать

Около квадрата описана окружность и в квадрат вписана окружность?

Около квадрата описана окружность и в квадрат вписана окружность.

Найдите отношение радиуса описанной окружности к радиусу вписанной окружнности.

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

1) Периметр правильного треугольника равен см?

1) Периметр правильного треугольника равен см.

Найдите радиус вписанной окружности.

2) Около квадрата описана окружность и в квадрат вписана окружность.

Найдите отношение радиуса описанной окружности к радиусу вписанной окружности.

Найдите сторону квадрата, вписанного в окружность радиуса корень из 8 — ми?

Найдите сторону квадрата, вписанного в окружность радиуса корень из 8 — ми.

На стороне правильного треугольника , вписанного в окружность с радиусом 4дм , построен квадрат ?

На стороне правильного треугольника , вписанного в окружность с радиусом 4дм , построен квадрат .

Найдите радиус окружности , описанной около этого квадрата .

С решением пожалуйста.

Перед вами страница с вопросом Найдите сторону квадрата вписанного в окружность радиуса 22 корень из 2?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Ответ : 14Пошаговое объяснение : CD = BD — BCCD = 27 + x — (3x + 47) = 27 + x — 3x — 47 = — 2x — 20CE = CD + DE = — 2x — 20 + 10 = — 2x — 10С другой стороны, СЕ = х + 26, x + 26 = — 2x — 103x = — 36x = — 12CE = x + 26 = — 12 + 26 = 14.

Решение в приложении.

ЕН⊥СН и EF⊥CF. Углы между соответственно перпендикулярными прямыми равны, значит∠FCH = ∠FEH. ВЕ = CF, значит ЕBCF — прямоугольник. BF — диагональ. Точка О — центр описанной окружности около прямоугольника. ∠FCH = ∠FEH значит FH — хорда окружност..

По теореме Пифагора 100 — 73 = 27. Сторона треугольника равна 2 корень из 27, или 6 корень из 3. Треугольник равносторонний. Расстояние от данной точки до плоскости треугольника — расстояние от точки до точки пересечения биссектрис (высот, медиан)..

16 — (5×2) = 6 6÷2 = 3 Друга сторона паралелограма 3см.

Sтрап. = ½(17 + 9)×4 = 13×4 = 52см².

12) С 16) А 17) D 18) С.

180 — 90 — 70 = 20 180 — (20 * 2) = 140 — один угол 180 — 140 = 40 — другой угол.

4, 2 / 6 = 0, 7 — будет равны две части, поделенные в серединке. 4, 2 — 0, 7 = 3, 5.

Значит угол B = углуD = 120 как противоположные в параллелограмме угол D находится между сторонами AD и DC значит можно воспользоваться формулою площади S = AD * DC * sinD = 12 * 32 / кор3 * кор3 / 2 = 192 см ^ 2 что такое кор3 / 2 это синус120.