Сторона квадрата описанного около окружности равна 8 см

Геометрия | 5 — 9 классы

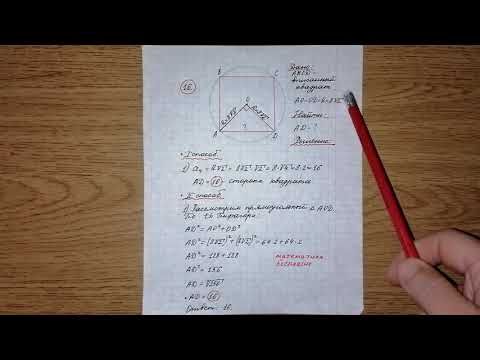
Квадрат со стороной 8 см описан около окружности.

Найдите площадь прямоугольного треугольника с острым углом 30 градусов, вписанного в данную окружность.

Диаметр окружности равен стороне квадрата, то есть D = 8.

Если в эту окружность вписан прямоугольный треугольник с углом 30 градусов, то гипотенуза у него — диаметр D = 8, один из катетов в 2 раза меньше, то есть 4, а второй катет находится по теореме Пифагора корень(8 ^ 2 — 4 ^ 2) = 4 * корень(3), площадь треугольника равна 4 * 4 * корень(3) / 2 = 8 * корень(3).

Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Площадь квадрата, вписанного в окружность, равна 16 см(в квадрате)?

Площадь квадрата, вписанного в окружность, равна 16 см(в квадрате).

Найдите площадь правильного треугольника, описанного около этой же окружности.

Видео:Найти площадь квадрата описанного около окружности радиуса 19Скачать

Около квадрата со стороной 2 корня из 2см описана окружность которая вписана в правильный треугольник?

Около квадрата со стороной 2 корня из 2см описана окружность которая вписана в правильный треугольник.

Найдите площадь треугольника.

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Площадь квадрата , описанного около окружности , равна 16 см2?

Площадь квадрата , описанного около окружности , равна 16 см2.

Найдите площадь правильного треугольника , вписанного в эту окружность .

Видео:16)Радиус окружности, описанной около квадрата, равен 8√2. Найдите длину стороны этого квадрата.Скачать

Сторона квадрата, вписанного в окружность, равно a см?

Сторона квадрата, вписанного в окружность, равно a см.

Найдите площадь правильного треугольника, описанного около данной окружности.

Видео:СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Описана окружность около прямоугольного треугольника с катетом А и прилежащим острым углом, равным ?

Описана окружность около прямоугольного треугольника с катетом А и прилежащим острым углом, равным .

Чему равна площадь окружности?

Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

В прямоугольный треугольник вписана окружность?

В прямоугольный треугольник вписана окружность.

Точка касания вписанной окружности с одним из катетов делит на отрезки 6си и 5см.

Найдите диаметр окружности, описанной около данного прямоугольного треугольника.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Сторона правильного шестиугольника, вписанного в окружность, равна 8см?

Сторона правильного шестиугольника, вписанного в окружность, равна 8см.

Найдите сторону квадрата, описанного около данной окружности.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Найти тангенсы острых углов прямоугольного треугольника зная что радиус вписанной окружности относится к радиусу описанной окружности около него окружности как 2 : 5?

Найти тангенсы острых углов прямоугольного треугольника зная что радиус вписанной окружности относится к радиусу описанной окружности около него окружности как 2 : 5.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Прямоугольный треугольник с гипотенузой 4 см вписан в окружность?

Прямоугольный треугольник с гипотенузой 4 см вписан в окружность.

Найдите площадь правильного шестиугольника, описанного около данной окружности.

Видео:Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Сторона квадрата, вписанного в окружность, равна а см?

Сторона квадрата, вписанного в окружность, равна а см.

Найдите площадь правильного треугольника, описанного около данной окружности.

Вы открыли страницу вопроса Квадрат со стороной 8 см описан около окружности?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Площадь основанияπR², а боковая поверхность 2πRH. 2πRH = 3 * πR² H = 1. 5R. .

S = AB * AC * sinA sinA = 1 / 2 S = (4 * 7) / 2 = 14.

Да, является. Т. к. Средняя линия делит противоположные стороны пополам.

1) 1 и 4 2) 180° — 13° = 167°, т. К. сумма смежных углов равна 180° 3)73°, т. К. вертикальные углы равны.

По теореме косинусов AC ^ 2 = AB ^ 2 + BC ^ 2 — 2 * AB * BC * COS45 COS45 = корень из 2 делить на 2 Подставляем получаем ответ.

Сумма боковых сторон = 180 гр⇒130, 50, 130, 50.

Плоские фигуры квадрат, ромб, прямоугольник, трапеция, параллелограмм, окружность, треугольник, многоугольник пространственные куб, параллелепипед, цилиндр, призма, пирамида, конус, шар.

Видео:Котлеты не готовлю! Вкуснее в жизне не ела! Меня научила этому ТРЮКУ бедный еврей! НЕВЕРОЯТНО ВКУСНОСкачать

Найдите длину окружности, описанной около квадрата со стороной 8 см.

Видео:№ 5.6. Периметр и площадь квадрата (дополнение)Скачать

Ваш ответ

Видео:Задание 3 ЕГЭ по математике. Урок 47Скачать

решение вопроса

Видео:2026 Найдите площадь квадрата описанного около окружности радиуса 14Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,006
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:ПЛОЩАДЬ КОЛЬЦА. Сделай выбор: на чьей ты стороне?Скачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:Как найти сторону квадрата в который вписаны 2 окружностиСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:Найдите площадь квадрата, описанного около окружности радиуса 4.Скачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Квадрат в окружности или окружность в квадрате #ShortsСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

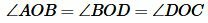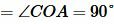(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

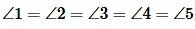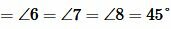(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).