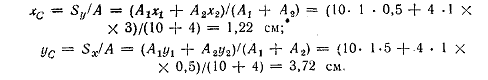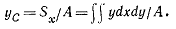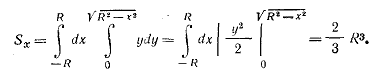Статический момент прямоугольного треугольника

Меню сайта

Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.

Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!

Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.

Лекции — теория, практика, задачи.

Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.

Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).

Книги — разная литература по теме.

Базовый курс лекций по сопромату, теория, практика, задачи.

1. Геометрические характеристики сечений.

1.1. Статический момент сечения.

При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления.

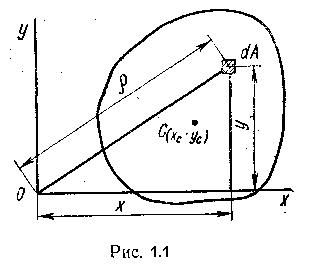
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида

(1.1)

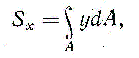
где y — расстояние от элементарной площадки dA до оси x.

Единицей измерения статического момента является единица длины в третьей степени, обычно см 3 (см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать

(1.2)

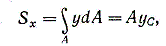
где А — площадь всей фигуры (равнодействующая); у с — расстояние от центра тяжести фигуры до оси х.

Из формулы (1.2) следует формула определения ординаты центра тяжести

Аналогично, статический момент относительно оси у равен

(1.4)

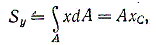
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.

Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями.

Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.

Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю.

Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:

(1.1a)

(1.4a)

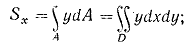
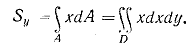
Здесь D — облать интегрирования.

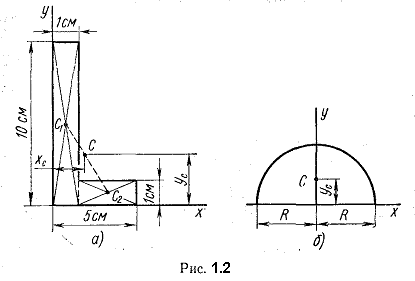
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а.

Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у.

По формулам (1.3) и (1.5) получим:

По этим координатам находим точку С — центр тяести сечения. Она лежит на линии, соединяющей точки С 1 и С 2 , ближе к фигуре, имеющей большую площадь.

Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б).

Решение. Пользуемся формулой

Вычисляем числитель, используя уравнение окружности х 2 + y 2 = R 2 :

Полезные ссылки

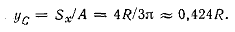
Видео:Техническая механика | Центр тяжести | Статический момент | Сечение компонентаСкачать

6.1. Статический момент площади сечения

6.1. СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ СЕЧЕНИЯ

Статический момент площади – распространенная на всю площадь сумма произведений элементарных площадок dA на расстояние от них до этой оси Это понятие аналогично моменту силы относительно оси. Если предположить, что А – вес пластины, имеющей форму нашего сечения, то статический момент Sz – это момент силы тяжести пластины относительно оси z. Размерность: единицы длины в третьей степени (см3; м3). Знаки: плюс, ноль и минус. Ось центральная – ось, относительно которой статический момент площади равен нулю. Центр тяжести сечения – точка пересечения центральных осей. Если фигура имеет ось симметрии, то эта ось является центральной. Статический момент составного сечения равен сумме статических моментов элементов этого сечения. Это следует из свойства определенного интеграла, который можно вычислять по частям – свойство аддитивности (от англ. add – прибавлять, присоединять, складывать). При известных статических Рис. 6.2. Связь знака статического момента площади с его положением в координатной системе моментах частей сечения можно найти координаты центра тяжести состав- ной фигуры: Пример 6.1. Определить положение центральных осей, параллельных основанию и высоте фигуры. Решение Разбиваем сложную фигуру на две простые, в конкретном примере – на два прямоугольника. Их центры тяжести расположены посредине высоты и посредине ширины. Координаты центров тяжести и площади простых фигур Статические моменты площадей простых фигур Координаты центра тяжести составной фигуры Через найденную точку проводим центральные оси zC и yC, параллельные основанию фигуры и ее высоте. Примечание. Центр тяжести фигуры, составленной из двух частей, лежит на линии, соединяющей центры тяжести простых фигур ее составляющих, причем расстояния до них обратно пропорциональны площадям простых фигур. Если сложная фигура составлена из нескольких простых, то общий центр тяжести находится внутри многоугольника, вершинами которого являются центры тяжести простых фигур.

Видео:Статический момент площади сечения (фигуры) относительно осиСкачать

Расчет геометрических характеристик плоских сечений простой формы

Этот онлайн калькулятор рассчитывает статические моменты, моменты инерции и радиусы инерции для плоских сечений простой формы

Данный онлайн калькулятор предназначен для вычисления основных геометрических характеристик простейших сечений. Калькулятор выводит пользователю статический момент, момент инерции и радиус инерции по осям x и y, а также координаты центра тяжести и площадь поперечного сечения. Теорию и формулы расчета можно найти под калькулятором.

Расчет геометрических характеристик плоских сечений простой формы

Левый нижний угол

Правый верхний угол

Центр

Радиус

Вершина при прямом угле

Вторая вершина

Третья вершина

Общий алгоритм расчета следующий:

1. Определение центра тяжести поперечного сечения
2. Определение площади поперечного сечения
3. Определение статического момента
4. Определение осевого момента инерции
5. Определение радиуса инерции

Статический моменты сечения , .

Физический смысл статического момента: если каждую простую фигуру, из которых состоит сложная фигура, наделить весом, то они будут представлять систему параллельных сил и каждая из них станет создавать свой момент относительно какой-либо оси с плечом, равным расстоянию от оси до центра тяжести данной простой фигуры. Если силу заменить площадью, то момент превратится из силового в геометрический показатель, называемый статическим моментом. 1 Измеряется в единицах длины в кубе (см³), может быть положительным, отрицательным и равным нулю.

В общем случае математическая запись статических моментов относительно оси x и y имеет вид:

Для частных случаев, когда рассматриваемая фигура представляет собой простую геометрическую, интегральная запись может быть заменена более простой, тогда формулы выглядят так:

где A — площадь поперечного сечения.
, — расстояние от осей x и y до центра тяжести простой фигуры.

Центр тяжести прямоугольника расположен в точке пересечения его диагоналей. Центр тяжести окружности совпадает непосредственно с центром самой окружности, а нахождение центра тяжести для треугольника можно найти в этом калькуляторе.

Осевой момент инерции

Осевой момент инерции площади сечения — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Величина осевого момента инерции всегда положительна. Формулы для осевого момента инерции:

Момент инерции фигуры относительно оси, проходящей через ее центр тяжести, называется центральным, или собственным, моментом инерции. Если фигура состоит из нескольких простых фигур, то оси, проведенные через центр тяжести всей фигуры, называются главными центральным осями. Моменты инерции относительно главных центральных осей называются главными центральными моментами.

Приведем формулы главных центральных моментов каждого из используемых в калькуляторе простейших сечений

Прямоугольник

1. Площадь поперечного сечения для прямоугольника находится по формуле: ,
   где b и h — стороны прямоугольника.
2. Моменты инерции и для прямоугольника находятся по формулам:

Для иллюстрации вывода формул центральных моментов рассмотрим вывод приведенной выше формулы главного центрального момента инерции для прямоугольника.

Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.
Главный центральный момент инерции относительно оси

Прямоугольный треугольник, катеты которого параллельны осям

1. Площадь поперечного сечения для прямоугольного треугольника находится по формуле: ,
   где b и h — катеты треугольника.
2. Моменты инерции и для треугольника находятся по формулам:

1. Площадь поперечного сечения для круга находится по формуле: ,
   где r — радиус окружности.
2. Моменты инерции и для круга находятся по формулам:

Для нахождения осевого момента инерции относительно произвольной оси воспользуемся теоремой Гюйгенса – Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр тяжести (центрального момента), и произведения площади тела на квадрат расстояния между осями. Измеряется в единицах длины в четвертой степени (см⁴).
Формулы:

Радиус инерции

Радиусом инерции i называют расстояние от соответствующей оси до точки, концентрация всей площади сечения в которой, даст такой же момент инерции, как и для всей площади рассматриваемой фигуры. Измеряется в единицах длины (см).

где A — площадь поперечного сечения,
, — осевые моменты инерции.

Техническая механика для строительных специальностей: учеб. пособие для студ. сред. проф. образования / В.И. Сетков — М.: Издательский центр «Академия», 2007. ↩

🎬 Видео

Статический моментСкачать

Определение центра тяжести сложной фигуры. СопроматСкачать

Сопротивление материалов. Лекция: геометрические характеристики сечений - статические моментыСкачать

Моменты инерции простейших фигур. Оси центральные и главные. Что это и где. #сопроматСкачать

Основы Сопромата. Геометрические характеристики поперечного сеченияСкачать

Моменты инерции Прямоугольника ► Вывод моментов инерции для прямоугольникаСкачать

Сопротивление материалов. Лекция: геометрические характеристики сечений - моменты инерцииСкачать

9.1. Геометрические характеристики плоских сечений. Общие сведения. Статический момент площадиСкачать

Моменты инерции сечения из простых фигурСкачать

Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Высота в прямоугольном треугольнике. 8 класс.Скачать

Момент инерцииСкачать

Основы сопромата. Задача 4. Момент инерции сложного сеченияСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Урок 94. Вычисление моментов инерции телСкачать

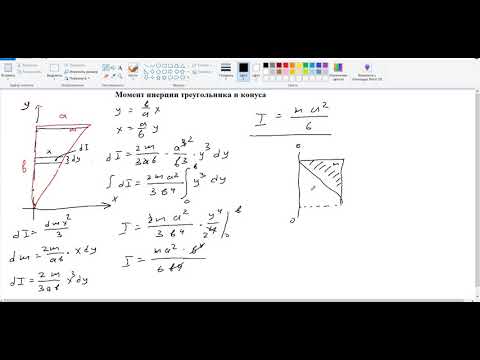
7. Момент инерции треугольника и конусаСкачать

Калькулятор геометрических характеристик сечений стержней 1. ТеорияСкачать

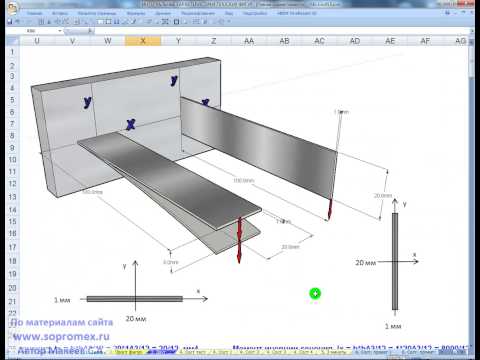
6. Определение характеристик сечения ( практический курс по сопромату )Скачать