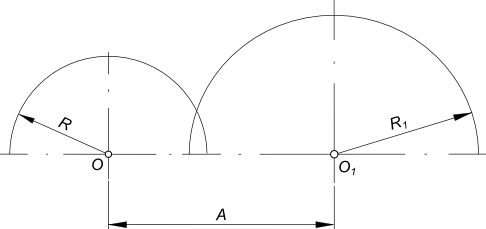
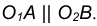Сопряжение дуг окружностей дугой окружности могут быть выполнены: — когда расстояние между центрами O и O1 сопрягаемых дуг больше суммы их радиусов R и R1, т. е. A>R+R1; — когда расстояние между центрами O и O1 сопрягаемых дуг меньше суммы их радиусов R и R1, т. е. R+R1>A. Во всех случаях решение задачи сводится к нахождению центра сопряжения O2 и точек сопряжения C и B.
Построим сопряжение дуг окружностей дугой окружности когда A>R+R1
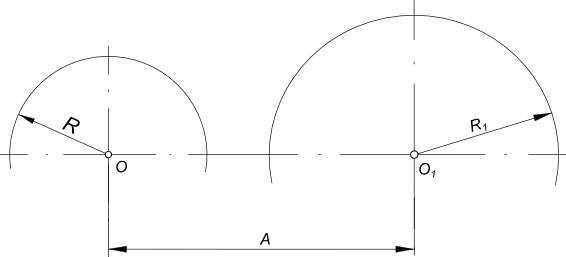
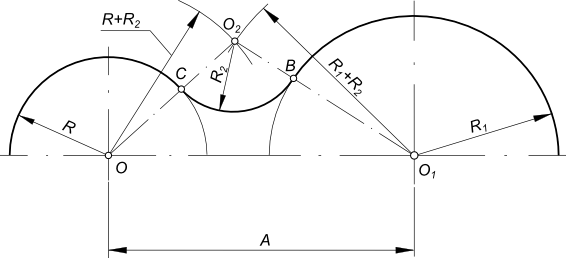
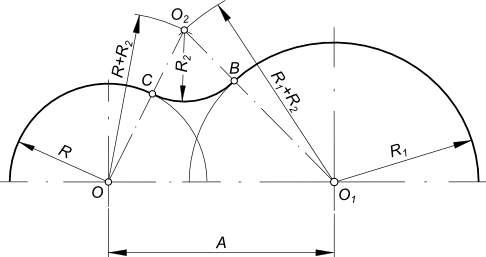
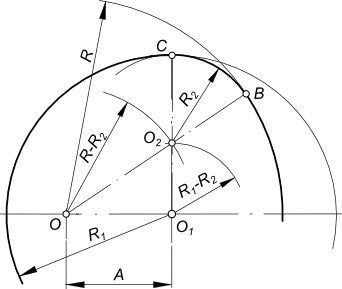
Заданы дуги окружностей радиусов R и R1 и расстояние между их центрами OO1 = A и радиус сопряжения R2. Находим центр сопряжения O2: — из центра O проводим дугу радиуса R+R2; — из центра O1 проводим дугу радиуса R1+R2. Пересечение этих дуг определит центр сопряжения O2.
Находим точки сопряжения C и B: — из точки O2 проводим прямые в центр O и O1; — находим на пересечении этих прямых с соответствующими дугами точки сопряжения C и B;
точки сопряжения C и B соединяем дугой радиуса R2.
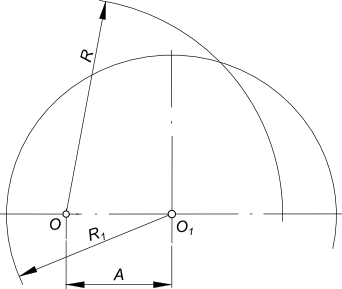
Для случая когда R+R1>A
построение выполняется аналогично
Построим сопряжение дуг окружностей дугой окружности когда A>R+R1
Заданы дуги окружностей радиусов R и R1 и расстояние между их центрами OO1 = A и радиус сопряжения R2. Находим центр сопряжения O2: — из центра O проводим дугу радиуса R2-R; — из центра O1 проводим дугу радиуса R2-R1. Пересечение этих дуг определит центр сопряжения O2.
Находим точки сопряжения C и B: — из точки O2 проводим прямые в центр O и O1; — находим на пересечении этих прямых с соответствующими дугами точки сопряжения C и B;
точки сопряжения C и B соединяем дугой радиуса R2.
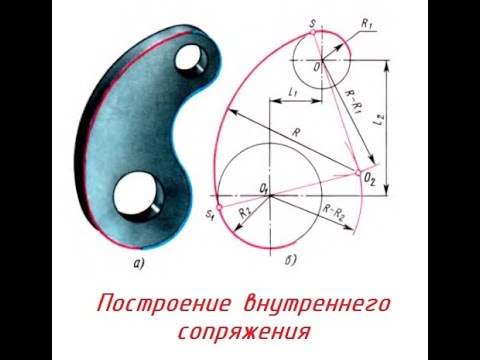
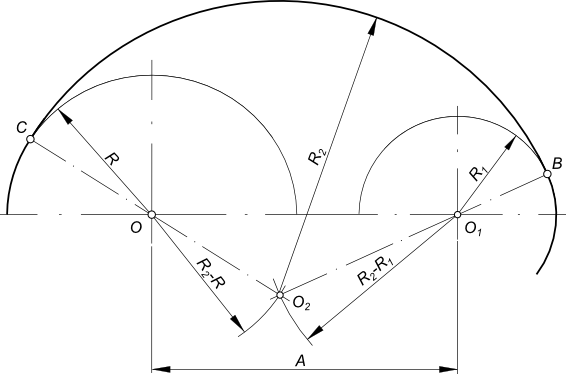
Сопряжение дуг окружностей дугой окружности когда R+R1>A Заданы дуги окружностей радиусов R и R1 и расстояние между их центрами OO1 = A и радиус сопряжения R2
Находим центр сопряжения O2: — из центра O проводим дугу радиуса R-R2; — из центра O1 проводим дугу радиуса R1-R2. Пересечение этих дуг определит центр сопряжения O2.
Находим точки сопряжения C и B: — из точки O2 проводим прямые в центр O и O1; — находим на пересечении этих прямых с соответствующими дугами точки сопряжения C и B;
точки сопряжения C и B соединяем дугой радиуса R2
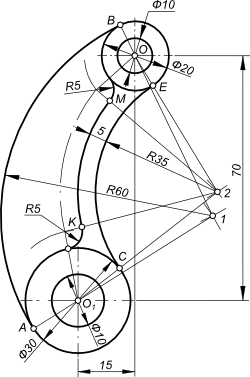
Применение приведенных выше примеров для построения сопряжений элементов рычага,
для построения сопряжений окружностей диаметров 20 и 30 мм дугами AB и EC радиусов R60 и R35 соответственно.
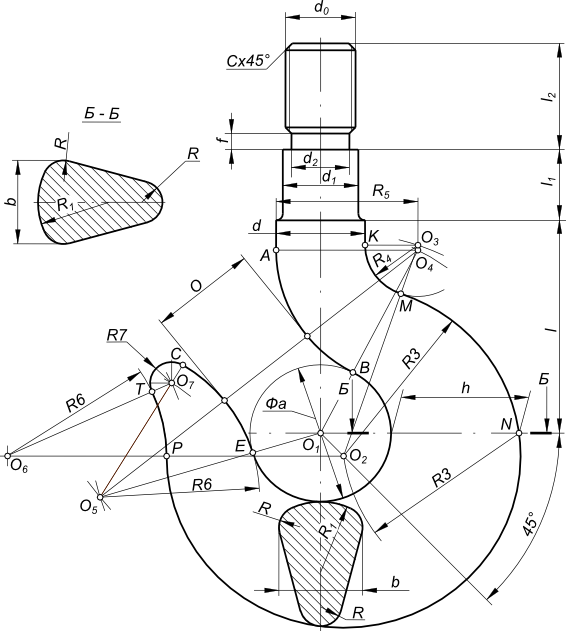
Применение приведенных выше примеров для построения сопряжений элементов однорогого крюка,
Заданы: фa40; b=24; h=36; d=25; d1=20; d2=16,4; d0=M20; l=60; l1=20; l2=30; R=6; R1=20; R2=20; R3=20; R4=15; R5=40; R6=45; R7=6,5; R8=2; c=2; f=4,5
Сопряжения крюка — это наиболее сложный пример на построение сопряжений. Вычерчивание крюка выполняем в следующем порядке: — проводим оси и вычерчиваем шейку крюка; — проводим из центра O1 пересечения осей основную окружность внутреннего очертания крюка. Радиус этой окружности равен a/2.; — находим центр O2 и проводим из него радиусом R3 основную дугу окружности внешнего очертания крюка. Для построения центра O2 проводим из центра O1 прямую n под углом 45 к осям и засекаем ее из точки N дугой окружности радиуса R3. Точка N удалена от центра O1 на расстояние h+a/2; — строим сопряжение внешней окружности правым прямолинейным контуром верхней части крюка. Сопрягаемая дуга имеет радиус R4. Центр сопряжения O3 и точки сопряжения K и M находим по общему правилу сопряжения дуги с прямой; — строим сопряжение внутренней окружности диаметра a с левым прямолинейным контуром верхней части крюка. Радиус сопряжения R4. Центр сопряжения O4 и точки сопряжения A и B определяются аналогично точкам O3, K и M; — строим очертания носка крюка. Пользуемся построениями приведенными на рисунках . и . . Находим центры O5, O6 и O7. Носок крюка должен касаться прямой e, проведенной на расстоянии m от горизонтальой оси крюка. Кроме того, зев крюка должен быть равен размеру O. Расстояние O измеряется по линии центров дуг O4O5, ограничивающих контур зева. Определяем центр O5 дуги радиуса R6. Для этого делаем две засечки: первую из центра O4 радиусом R5+R6+O; вторую — из центра O1 радиусом a/2+R6. Точка сопряжения E лежит на линии центров O1 — O5. Из центра O5 проводим дугу радиуса R6, начиная от точки E. Находим центр O7 дуги радиуса R7. Засекаем дугой радиуса R6-R7 из центра O5 и засекаем дугой радиуса R6-R7 из центра O6. Точка сопряжения C лежит на линии центров O5 — O7. Проводим из центра O7 дугу радиуса R7. Определяем центр O6 дуги радиса R6, сопрягающей носок крюка с внешним контуром крюка. Для этого делаем засечку из центра O2 радиусом R3+R6. Точки сопряжений T и P лежат на линии центров O6 — O7 и O6 — O2. Из центра O4 проводим дугу, соединяющую точки T и P.
Видео:Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение (касание) окружностей
Различают внешнее (рис. 1.18, а) и внутреннее (рис. 1.18, б) касания окружностей.
Основные свойства касающихся окружностей;
- 1) точка касания К лежит на линии, соединяющей центры касающихся окружностей (линии центров);
- 2) при внешнем касании расстояние между центрами касающихся окружностей
при внутреннем касании

Рис. 1.18. Касание двух окружностей:
а — внешнее касание; б — внутреннее касание
Сопряжение двух окружностей дугой заданным радиусом Внешнее касание. При внешнем касании (рис. 1.19) из центров О, и 02 проводят две вспомогательные окружности радиусами R< + R и R2 + R, где R — радиус заданной дуги. Точка пересечения вспомогательных окружностей — точка О является центром сопрягающей дуги. Для определения местоположения точек касания /С, и К2 проводят две линии центров 001 и 002.
Рис. 1.19. Сопряжение двух окружностей при внешнем касании
Внутреннее касание. При внутреннем касании (рис. 1.20) вспомогательные окружности из центров данных окружностей проводятся радиусами R — R< и R — Rr
Рис. 1.20. Сопряжение двух окружностей при внутреннем касании
Внешне-внутреннее касание. Построение внешне-внутреннего касания окружностей дугой заданным радиусом R показано на рис. 1.21.
Построение сопряжений дугой окружности радиусом Rx, определяемым построением, рассмотрим на следующем примере.
Рис. 1.21. Внешне-внутреннее касание окружностей дугой заданным радиусом R
Пример 1.1. Постройте сопряжения дугой окружности радиусом Ry, определяемым построением. На рис. 1.22 приведены исходные данные для построения:
- • окружность (или дуга) известным радиусом R с центром в точке О;
- • точка В, через которую проходит дуга сопряжения с первоначально неизвестным радиусом Rx;
- • линия р, на которой находится центр сопрягающей дуги.
Рис. 1.22. Исходные данные к примеру 1.1
Решение. Решим задачу способом вспомогательной окружности, концентричной с искомой (рис. 1.23).
При внутреннем касании заданной и искомой окружности (рис. 1.23, а) радиус вспомогательной окружности меньше радиуса искомой на величину R. при внешнем (рис. 1.23,6) — больше на эту величину.
Выполняем построения, действуя в таком порядке:
1) отмечаем точку М (на расстоянии R от точки В);
Рис. 1.23. Сопряжение дугой окружности радиусом Rx способом вспомогательной концентрической окружности:
а — внутреннее касание; б — внешнее касание
- 2) соединяем точки М и О и, рассматривая отрезок ОМ как хорду вспомогательной окружности, проводим перпендикуляр через его середину до пересечения с линией р в точке О,;
- 3) проводим линию центров 0,0 и определяем точку К касания заданной и искомой окружностей; (К = Rx.
Видео:1 2 4 сопряжение окружностейСкачать

Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
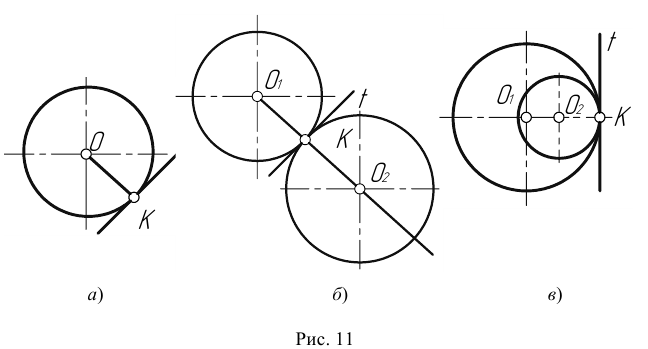
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Точка касания К и центры окружностей
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Видео:Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение двух пересекающихся прямых линий
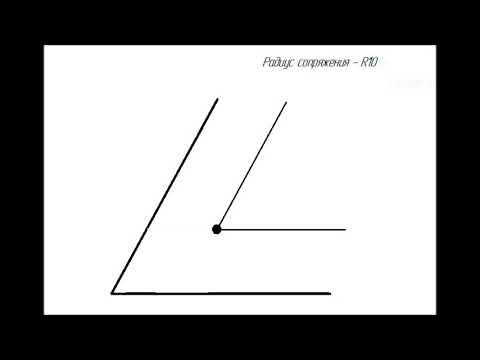
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Видео:Сопряжение двух окружностейСкачать

Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 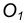
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
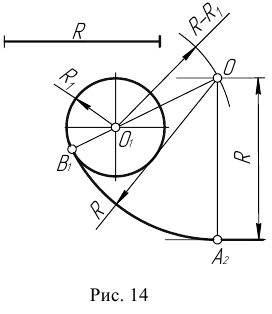
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 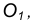
Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 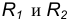
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 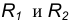
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Видео:Сопряжение окружностейСкачать

Построение касательных
Пример 1. Дана окружность с центром в точке 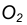
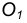
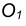
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 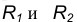
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💡 Видео
Смешанное сопряжение двух дуг окружностей третьей дугой. Урок15.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Сопряжение окружностей #черчение #сопряжениеСкачать

Внешнее сопряжение двух окружностейСкачать
Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение прямой с окружностьюСкачать

Построение ВНЕШНЕГО СОПРЯЖЕНИЯСкачать
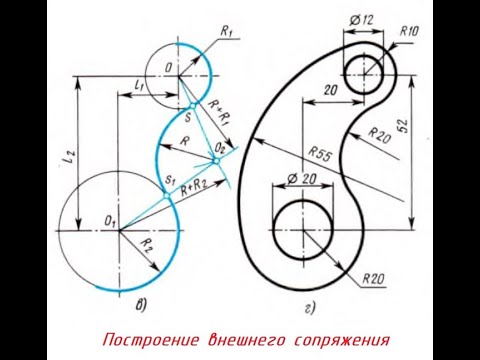
СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]Скачать
![СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]](https://i.ytimg.com/vi/oKj3m1n67wI/0.jpg)
Сопряжение острого углаСкачать
Построение ВНУТРЕННЕГО СОПРЯЖЕНИЯСкачать
Инженерная графика. 2 урок. Построение сопряженийСкачать

Внутреннее сопряжение двух окружностейСкачать

Внутреннее сопряжение дуги и прямой дугой заданного радиуса.Урок17.(Часть1.ГЕОМЕТРИЧЕСКИЕПОСТРОЕНИЯ)Скачать

Смешанное сопряжение двух окружностейСкачать









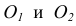
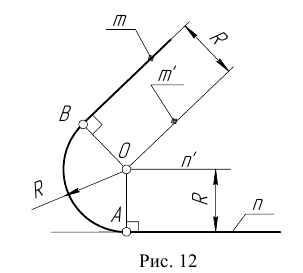
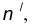 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.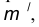 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.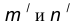 найдем центр сопряжения О.
найдем центр сопряжения О.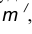 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.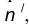 проведенная радиусом
проведенная радиусом 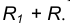
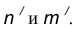
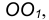 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.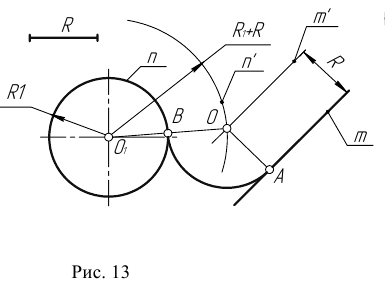
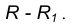
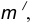 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 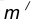 равен
равен 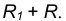
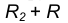 проведем окружность
проведем окружность 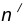 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.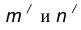 .
.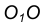 с дугой m.
с дугой m.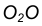 с дугой n .
с дугой n .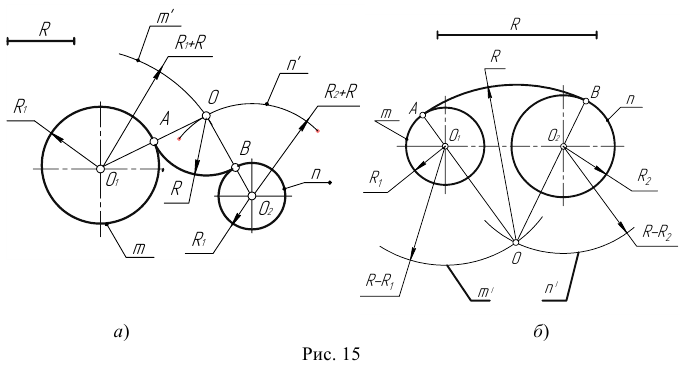
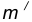 на расстоянии
на расстоянии 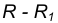 от данной окружности m.
от данной окружности m.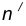 на расстоянии
на расстоянии 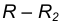 от данной окружности n.
от данной окружности n.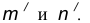
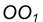 с заданной окружностью m.
с заданной окружностью m. c заданной окружностью n.
c заданной окружностью n.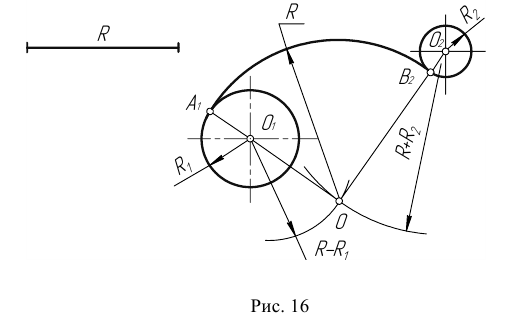
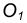 с центром окружности
с центром окружности 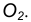
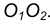
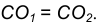
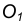 с точкой А.
с точкой А.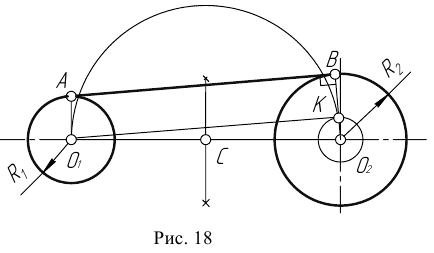
 проведем вспомогательную окружность.
проведем вспомогательную окружность. проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 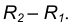
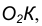 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем