Смежный угол равнобедренного треугольника

Чему равен внешний угол равнобедренного треугольника? Какие у него свойства?

Как и для всякого треугольника, внешний угол при любой вершине равнобедренного треугольника равен сумме двух внутренних углов, не смежных с ним.

Помимо этого, внешние углы равнобедренного треугольника имеют свои свойства.

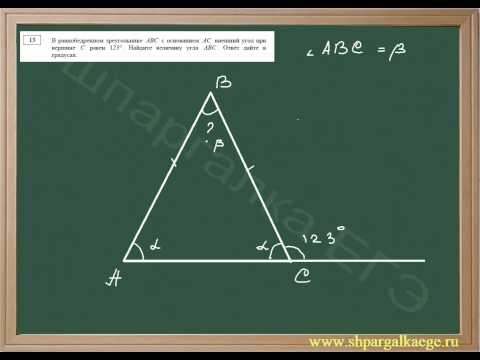
Внешний угол при вершине равнобедренного треугольника в два раза больше внутреннего угла при его основании.

Дано: ∆ ABC, AC=BC,

∠BCF — внешний угол при вершине C.

Так как внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним, то

Поскольку ∠A=∠B (как углы при основании равнобедренного треугольника), то

Что и требовалось доказать.

Внешний угол при основании равнобедренного треугольника на 90º больше половины внутреннего угла при его вершине.

Дано: ∆ ABC, AC=BC,

∠NBC — внешний угол при вершине B.

Доказать: ∠NBC=1/2 ∠C +90º.

1) ∠A=∠ABC (как углы при основании равнобедренного треугольника).

Отсюда ∠NBC=180º-∠ABC=180º-(90º-1/2 ∠C)=90º+ 1/2 ∠C.

Видео:№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать

Что такое смежные углы: определение, теорема, свойства

В данной публикации мы рассмотрим, что из себя представляют смежные углы, приведем формулировку теоремы касательно них (в т.ч. следствия из нее), а также перечислим тригонометрические свойства смежных углов.

Видео:№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Определение смежных углов

Два прилежащих угла, внешними сторонами образующие прямую, называется смежными. На рисунке ниже это углы α и β.

Если два угла имеют одну общую вершину и сторону, они являются прилежащими. При этом внутренние области этих углов не должны пересекаться.

Принцип построения смежного угла

Одну из сторон угла протягиваем через вершину дальше, в результате чего образуется новый угол, смежный с исходным.

Видео:Определение угла равнобедренного треугольникаСкачать

Теорема о смежных углах

Сумма градусов смежных углов равняется 180°.

Смежн. угол 1 + Смежн. угол 2 = 180°

Пример 1
Один из смежных углов равняется 92°, чему равен второй?

Решение, согласно рассмотренной выше теореме, очевидно:
Смежн. угол 2 = 180° – Смежн. угол 1 = 180° – 92° = 88°.

Следствия из теоремы:

• Смежные углы двух равных углов равны между собой.
• Если угол является смежным с прямым (90°), значит он также равен 90°.
• Если угол является смежным с острым, значит он больше 90°, т.е. является тупым (и наоборот).

Пример 2
Допустим, у нас есть угол, смежный с 75°. Он должен быть больше 90°. Давайте проверим это.

Воспользовавшись теоремой, находим значение второго угла:
180° – 75° = 105°.

105° > 90°, следовательно угол является тупым.

Видео:Внешний угол треугольникаСкачать

Тригонометрические свойства смежных углов

1. Синусы смежных уголов равны, т.е. sin α = sin β.
2. Величины косинусов и тангенсов смежных углов равны, но имеют противоположные знаки (кроме неопределенных значений).
   • cos α = -cos β.
   • tg α = -tg β.

Видео:Задача 1 Внешний угол равнобедренного треугольникаСкачать

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Готовиться с нами — ЛЕГКО!

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Эффективное решение существует!

Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.

Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.

После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.

Факт 1.
(bullet) Смежные углы — два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.

Смежные углы: (angle AOB) и (angle BOC) .
Теорема: Сумма смежных углов равна (180^circ) : (angle AOB+angle BOC=180^circ) .

Факт 2.
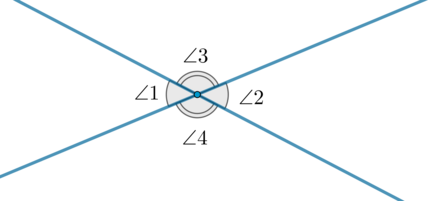
(bullet) Вертикальные углы — два угла, у которых стороны одного угла являются продолжениями сторон другого (образуются, например, при пересечении двух прямых).

Вертикальные углы: (angle 1) и (angle 2) , (angle 3) и (angle 4) .
Теорема: Вертикальные углы равны: (angle 1=angle 2) и (angle 3=angle 4) .

Факт 3.
(bullet) Сумма углов (angle A, angle B, angle C) треугольника (ABC) равна (180^circ) .
(bullet) Внешний угол (angle BCD) треугольника (ABC) равен сумме двух углов треугольника, не смежных с ним.

Факт 4.
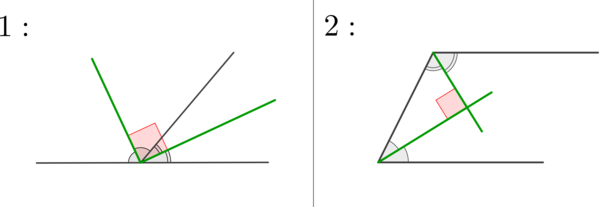
(bullet) Биссектрисы смежных углов взаимно перпендикулярны.
(bullet) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.

Факт 5.
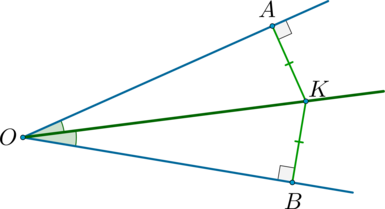
(bullet) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
(bullet) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Факт 6.
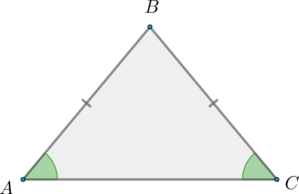
(bullet) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:

Второе свойство равнобедренного треугольника: углы при основании равны.

Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
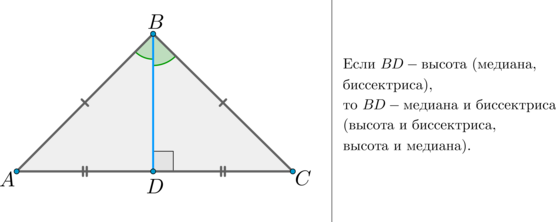
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.

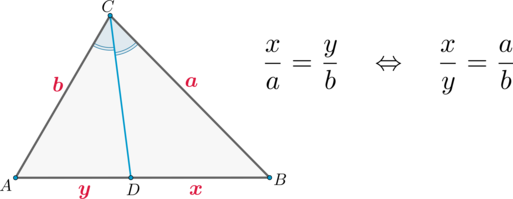
Факт 7.
(bullet) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

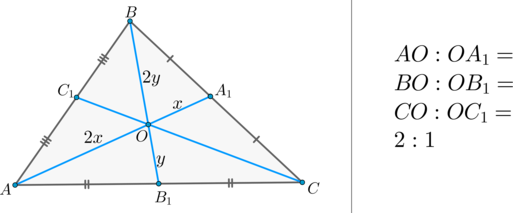
Факт 8.
(bullet) Медианы в треугольнике точкой пересечения делятся в отношении (2:1) , считая от вершины.

Факт 9.
(bullet) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

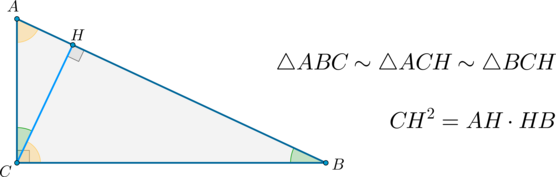
Факт 10.
(bullet) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
(bullet) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.

Факт 11.
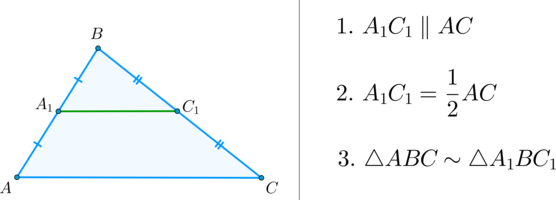
(bullet) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
(bullet) 1. Средняя линия треугольника параллельна третьей стороне.
(bullet) 2. Средняя линия треугольника равна половине третьей стороны.
(bullet) 3. Средняя линия отсекает от треугольника подобный ему треугольник.

Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.

Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?

1. Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
2. Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.

Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

🔍 Видео

№227. Найдите углы равнобедренного треугольника, если: а) угол при основании в два разаСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

Равнобедренный треугольник. 7 класс.Скачать

7 класс, 11 урок, Смежные и вертикальные углыСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Найти угол равнобедренного треугольникаСкачать

Смежные углы. 7 класс.Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

№225. Докажите, что каждый угол равностороннего треугольника равен 60°.Скачать

Один из внешних углов равнобедренного треугольника равен 80 градусов Найдите углы этого треугольникСкачать

Урок 2 | Виды углов | Равнобедренный треугольник | Сумма углов в треугольнике | Внешний уголСкачать