Случайные точки в окружности python

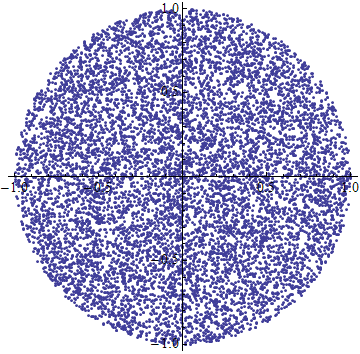
Мне нужно создать равномерно случайную точку в радиусе круга R .

Я понимаю это, просто выбирая равномерно случайный угол в интервале [0 . 2π) и равномерно случайный радиус в интервале (0 . R ), я получу больше точек к центру, поскольку для двух данных радиусы, точки в меньшем радиусе будут ближе друг к другу, чем для точек в большем радиусе.

Я нашел запись в блоге по этому поводу здесь , но я не понимаю его рассуждения. Я полагаю, это правильно, но мне бы очень хотелось понять, откуда он получает (2 / R 2 ) × r и как он получает окончательное решение.

Обновление: 7 лет после публикации этого вопроса я все еще не получил удовлетворительного ответа на фактический вопрос относительно математики позади алгоритма квадратного корня. Так что я потратил день на написание ответа сам. Ссылка на мой ответ .

Давайте подойдем к этому, как Архимед.

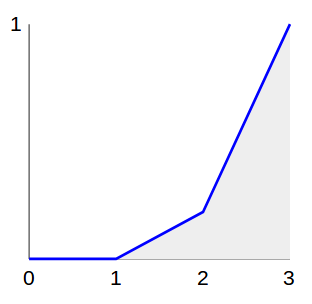
Как мы можем сгенерировать точку равномерно в треугольнике ABC, где | AB | = | BC |? Давайте сделаем это проще, расширив параллелограмм ABCD. В ABCD легко генерировать точки равномерно. Мы равномерно выбираем случайную точку X на AB и Y на BC и выбираем Z таким, что XBYZ является параллелограммом. Чтобы получить равномерно выбранную точку в исходном треугольнике, мы просто складываем любые точки, которые появляются в АЦП, обратно в АВС вдоль АС.

Теперь рассмотрим круг. В пределе мы можем рассматривать его как бесконечно много равнобедренных треугольников ABC с B в начале координат и A и C на окружности, исчезающе близко друг к другу. Мы можем выбрать один из этих треугольников, просто выбрав угол тета. Итак, теперь нам нужно сгенерировать расстояние от центра, выбрав точку в полоске ABC. Снова продлим до ABCD, где D теперь в два раза больше радиуса от центра круга.

Выбрать случайную точку в ABCD легко, используя описанный выше метод. Выберите случайную точку на AB. Равномерно выбрать случайную точку на BC. То есть. Выберите пару случайных чисел x и y равномерно на [0, R], давая расстояния от центра. Наш треугольник является тонкой полоской, поэтому AB и BC по существу параллельны. Таким образом, точка Z — это просто расстояние x + y от начала координат. Если x + y> R, мы сбрасываем обратно.

Вот полный алгоритм для R = 1. Я надеюсь, вы согласны, что это довольно просто. Он использует триггер, но вы можете дать гарантию того, сколько времени это займет и сколько random() вызовов ему нужно, в отличие от выборки отклонения.

Вот это в Mathematica.

Видео:33 Задача: Принадлежит ли точка кругу с центром в начале координат?Скачать

Как создать случайную точку внутри круга радиуса R :

(Предполагается, что random() дает значение между 0 и 1 равномерно)

Если вы хотите преобразовать это в декартовы координаты, вы можете сделать

Видео:#65. Модуль random стандартной библиотеки | Python для начинающихСкачать

Зачем sqrt(random()) ?

Давайте посмотрим на математику, которая приводит к sqrt(random()) . Предположим для простоты, что мы работаем с единичным кругом, т.е. R = 1.

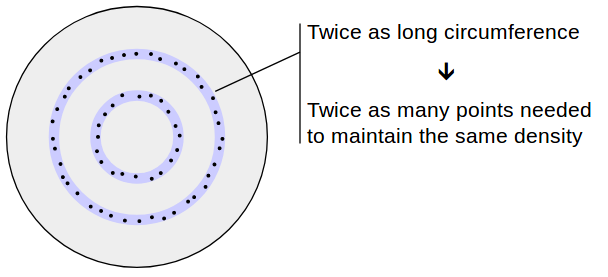
Среднее расстояние между точками должно быть одинаковым независимо от того, как далеко от центра мы смотрим. Это означает, например, что, глядя на периметр окружности с окружностью 2, мы должны найти вдвое больше точек, чем количество точек на периметре окружности с окружностью 1.

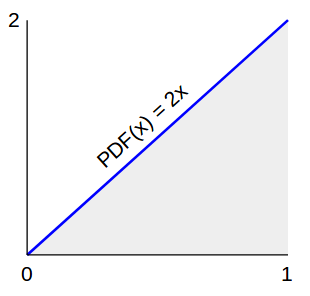
Поскольку окружность круга (2π r ) растет линейно с ростом r , отсюда следует, что число случайных точек должно расти линейно с ростом r . Другими словами, искомая функция плотности вероятности (PDF) растет линейно. Так как PDF должен иметь площадь, равную 1, а максимальный радиус равен 1, мы имеем

Итак, мы знаем, как должна выглядеть желаемая плотность наших случайных значений. Теперь: как мы можем генерировать такое случайное значение, когда все, что у нас есть, это равномерное случайное значение между 0 и 1?

1. Из PDF создайте накопительную функцию распределения (CDF)
2. Отразите это вдоль y = x
3. Примените полученную функцию к равномерному значению от 0 до 1.

Звучит сложно? Позвольте мне вставить цитату с небольшой боковой дорожкой, которая передает интуицию:

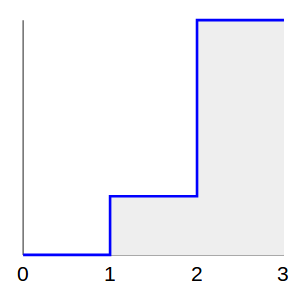
Предположим, мы хотим сгенерировать случайную точку со следующим распределением:

• 1/5 баллов равномерно между 1 и 2, и
• 4/5 баллов равномерно между 2 и 3.

CDF — это, как следует из названия, кумулятивная версия PDF. Интуитивно понятно: в то время как PDF ( x ) описывает количество случайных значений в точке x , CDF ( x ) описывает количество случайных значений меньше значения x .

В этом случае CDF будет выглядеть так:

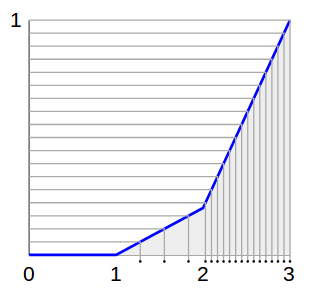
Чтобы увидеть, как это полезно, представьте, что мы стреляем пулями слева направо на равномерно распределенных высотах. Когда пули попадают в линию, они падают на землю:

Посмотрите, как плотность пуль на земле соответствует нашему желаемому распределению! Мы почти там!

Проблема в том, что для этой функции ось y является выходной, а ось x является входной . Мы можем только «стрелять пулями прямо с земли»! Нам нужна обратная функция!

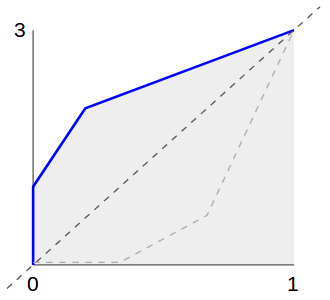
Вот почему мы отражаем все это; х становится у, а у становится х :

Мы называем это CDF -1 . Чтобы получить значения в соответствии с желаемым распределением, мы используем CDF -1 (random ()).

… Итак, вернемся к генерации случайных значений радиуса, где наш PDF равен 2 х .

Шаг 1: Создайте CDF: так

как мы работаем с реалами, CDF выражается как интеграл PDF.

Шаг 2: Зеркально отразите CDF вдоль y = x :

Математически это сводится к обмену x и y и решению для y :

Шаг 3: применить полученную функцию к равномерному значению от 0 до 1

CDF -1 (random ()) = √random ()

Что мы и собираемся извлечь 🙂

Вот быстрое и простое решение.

Выберите два случайных числа в диапазоне (0, 1), а именно a и b . Если b поменять их. Ваша точка зрения (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)) .

Вы можете думать об этом решении следующим образом. Если вы возьмете круг, обрежете его, а затем выпрямите, вы получите прямоугольный треугольник. Уменьшите этот треугольник, и вы получите треугольник от (0, 0) до (1, 0) до (1, 1) и обратно до (0, 0) . Все эти преобразования изменяют плотность равномерно. То, что вы сделали, равномерно выбрали случайную точку в треугольнике и полностью изменили процесс, чтобы получить точку в круге.

Обратите внимание на плотность точек пропорционально обратному квадрату радиуса, поэтому вместо того, чтобы выбирать r из [0, r_max] , выберите из [0, r_max^2] , а затем вычислите ваши координаты как:

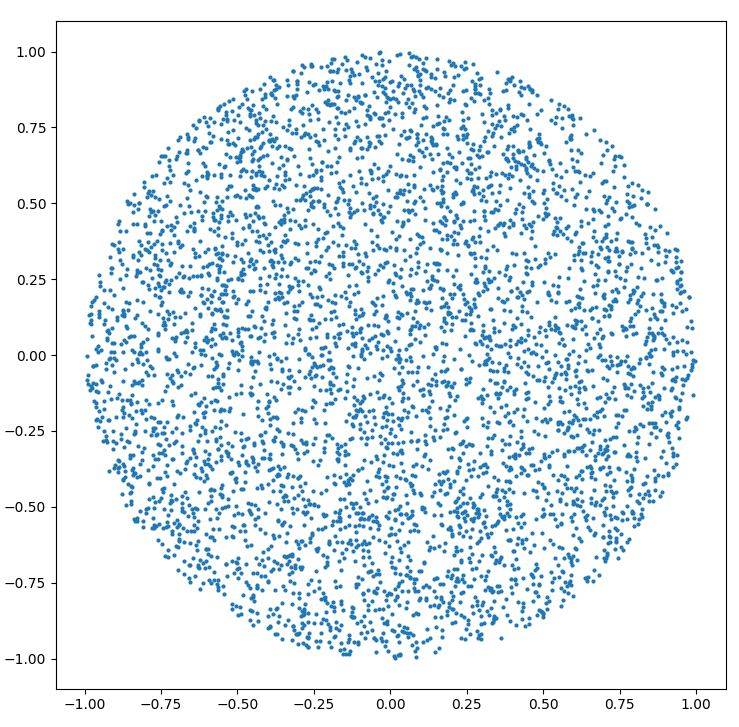
Это даст вам равномерное распределение точек на диске.

Подумайте об этом таким образом. Если у вас есть прямоугольник, где одна ось является радиусом, а другая — углом, и вы берете точки внутри этого прямоугольника, которые близки к радиусу 0. Все они будут располагаться очень близко к началу координат (то есть близко друг к другу на окружности.) Однако, точки около радиуса R, все они будут падать около края круга (то есть далеко друг от друга).

Это может дать вам некоторое представление о том, почему вы получаете такое поведение.

Коэффициент, полученный по этой ссылке, говорит вам, сколько соответствующей области в прямоугольнике нужно отрегулировать, чтобы она не зависела от радиуса после его сопоставления с окружностью.

Редактировать: Итак, он пишет в ссылке, которой вы делитесь: «Это достаточно легко сделать, рассчитав обратное кумулятивному распределению, и мы получим для r:».

Основным условием здесь является то, что вы можете создать переменную с желаемым распределением из униформы, отобразив униформу с помощью обратной функции кумулятивной функции распределения желаемой функции плотности вероятности. Зачем? Просто пока принимайте это как должное, но это факт.

Вот мое интуитивное объяснение математики. Функция плотности f (r) по отношению к r должна быть пропорциональна самой r. Понимание этого факта является частью любой основной книги исчисления. Смотрите разделы об элементах полярной зоны. Некоторые другие постеры упоминали об этом.

Поэтому мы назовем это f (r) = C * r;

Это оказывается большая часть работы. Теперь, поскольку f (r) должна быть плотностью вероятности, вы можете легко увидеть, что, интегрируя f (r) по интервалу (0, R), вы получите, что C = 2 / R ^ 2 (это упражнение для читателя .)

Таким образом, f (r) = 2 * r / R ^ 2

Хорошо, вот как вы получите формулу в ссылке.

Затем последняя часть идет от равномерной случайной величины u в (0,1), которую необходимо отобразить с помощью обратной функции кумулятивной функции распределения от этой требуемой плотности f (r). Чтобы понять, почему это так, вам нужно найти расширенный вероятностный текст, такой как, вероятно, папулис (или получить его самостоятельно).

Интегрируя f (r), вы получите F (r) = r ^ 2 / R ^ 2

Чтобы найти обратную функцию этого, вы устанавливаете u = r ^ 2 / R ^ 2, а затем решаете для r, что дает вам r = R * sqrt (u)

Это также имеет смысл интуитивно, u = 0 должно отображаться на r = 0. Кроме того, u = 1 должно отображаться на r = R. Кроме того, оно идет по функции квадратного корня, которая имеет смысл и соответствует ссылке.

Причина, по которой наивное решение не работает, заключается в том, что оно дает более высокую плотность вероятности точкам, расположенным ближе к центру круга. Другими словами, у круга, который имеет радиус r / 2, есть вероятность r / 2 получить выбранную точку, но у него есть область (количество точек) pi * r ^ 2/4.

Поэтому мы хотим, чтобы плотность вероятности радиуса имела следующее свойство:

Вероятность выбора радиуса, меньшего или равного данному r, должна быть пропорциональна площади круга с радиусом r. (потому что мы хотим иметь равномерное распределение по точкам, а большие области означают больше точек)

Другими словами, мы хотим, чтобы вероятность выбора радиуса между [0, r] была равна его доле от общей площади круга. Общая площадь круга равна pi * R ^ 2, а площадь круга с радиусом r равна pi * r ^ 2. Таким образом, мы хотели бы, чтобы вероятность выбора радиуса между [0, r] была (pi * r ^ 2) / (pi * R ^ 2) = r ^ 2 / R ^ 2.

Теперь приходит математика:

Вероятность выбора радиуса между [0, r] является интегралом p (r) dr от 0 до r (это просто потому, что мы добавляем все вероятности меньших радиусов). Таким образом, мы хотим, чтобы интеграл (p (r) dr) = r ^ 2 / R ^ 2. Мы можем ясно видеть, что R ^ 2 является константой, поэтому все, что нам нужно сделать, это выяснить, какой p (r) при интеграции даст нам что-то вроде r ^ 2. Ответ явно г * постоянный. интеграл (r * постоянная dr) = r ^ 2/2 * постоянная. Это должно быть равно r ^ 2 / R ^ 2, поэтому константа = 2 / R ^ 2. Таким образом, у вас есть распределение вероятности p (r) = r * 2 / R ^ 2

Примечание. Другой, более интуитивно понятный способ осмыслить проблему — представить, что вы пытаетесь присвоить каждому кругу радиус вероятности плотности ra, равный пропорции числа точек на его окружности. Таким образом, окружность с радиусом r будет иметь 2 * pi * r «точки» на своей окружности. Общее количество баллов: pi * R ^ 2. Таким образом, вы должны дать окружности ra вероятность, равную (2 * pi * r) / (pi * R ^ 2) = 2 * r / R ^ 2. Это намного проще для понимания и более интуитивно понятно, но не совсем математически обоснованно.

Пусть ρ (радиус) и φ (азимут) — две случайные величины, соответствующие полярным координатам произвольной точки внутри окружности. Если точки распределены равномерно, то какова функция распределения ρ и φ?

Для любого r: 0 2

Где S1 и S0 — площади круга радиуса r и R соответственно. Таким образом, CDF может быть дан как:

Обратите внимание, что для R = 1 случайная величина sqrt (X), где X равномерно на [0, 1), имеет этот точный CDF (потому что P [sqrt (X) — англичанин, иммигрировавшие в Австралии
источник

Это действительно зависит от того, что вы подразумеваете под «равномерно случайным». Это тонкий момент, и вы можете узнать больше об этом на странице вики здесь: http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29 , где та же проблема, давая различные интерпретации для «равномерно случайных» дает разные ответы!

В зависимости от того, как вы выбираете точки, распределение может варьироваться, даже если они в некоторых смысле .

Кажется, что запись в блоге пытается сделать ее равномерно случайной в следующем смысле: если вы возьмете под круг окружности с тем же центром, то вероятность того, что точка попадет в эту область, пропорциональна площади область. Я полагаю, что это попытка следовать принятой в настоящее время стандартной интерпретации «равномерно случайных» для 2D-областей с определенными на них областями : вероятность падения точки в любом регионе (с четко определенной областью) пропорциональна площади этого региона.

Видео:Алгоритмы. Попадание точки в кругСкачать

Генерировать случайную точку внутри круга (равномерно)

Мне нужно создать равномерно случайную точку в пределах круга радиуса R.

Я понимаю, что просто выбирая равномерно случайный угол в интервале [0 . 2π) и равномерно случайный радиус в интервале (0 . R) Я бы закончил с большим количеством точек к центру, так как для двух заданных радиусов точки меньшего радиуса будут ближе друг к другу, чем для точек большего радиуса.

Я нашел запись в блоге это здесьЯ бы очень хотел понять, откуда он получает (2/R 2 )×r и как он получает окончательное решение.

обновление: через 7 лет после публикации этого вопроса я все еще не получил удовлетворительного ответа на фактический вопрос о математике алгоритма квадратного корня. Так я провел день сам пишу ответ. ссылка на мой ответ.

Видео:Плавающая точка наносит ответный ударСкачать

21 ответов

давайте как Архимед бы.

как мы можем генерировать точку равномерно в треугольнике ABC, где / AB / =|BC/? Давайте упростим это, распространившись на параллелограмм ABCD. Легко генерировать точки равномерно в ABCD. Мы равномерно выбираем случайную точку X на AB и Y на BC и выбираем Z такой, что XBYZ является параллелограммом. Чтобы получить равномерно выбранную точку в исходном треугольнике, мы просто складываем все точки, которые появляются в АЦП, обратно в ABC вдоль ПЕРЕМЕННЫЙ ТОК.

Теперь рассмотрим кругу. В пределе мы можем думать о нем как о бесконечном множестве изоцелевых треугольников ABC с B в начале и A и C на окружности, исчезающе близких друг к другу. Мы можем выбрать один из этих треугольников, просто выбрав угол тета. Поэтому теперь нам нужно сгенерировать расстояние от центра, выбрав точку в Щепке ABC. Опять же, распространитесь на ABCD, где D теперь вдвое больше радиуса от центра круга.

выбор случайной точки в ABCD используя описанный выше метод. Выберите случайную точку на AB. Равномерно выберите случайную точку на BC. То есть. выберите пару случайных чисел X и y равномерно на [0, R], дающих расстояния от центра. Наш треугольник представляет собой тонкую полоску, поэтому AB и BC по существу параллельны. Таким образом, точка Z-это просто расстояние x+y от начала координат. Если x+y>R, мы складываемся обратно.

вот полный алгоритм для R=1. Надеюсь, вы согласитесь, что все очень просто. Он использует trig, но вы можете дать гарантию на сколько времени он будет возьмите, а сколько random() вызывает его потребности, не похож на забор сброса.

вот он в Mathematica.

Видео:Попадание точки в заданную область. Два сектора. Уроки программирования на С++.Скачать

как создать случайную точку в пределах круга радиуса R:

(если random() дает значение между 0 и 1 равновероятно)

если вы хотите преобразовать это в Декартовые координаты, вы можете сделать

Видео:Рисуем с Python — Случайные числаСкачать

почему sqrt(random()) ?

давайте посмотрим на математику, которая приводит к sqrt(random()) . Предположим для простоты, что мы работаем с единичным кругом, т. е. R = 1.

среднее расстояние между точками должно быть одинаковым независимо от того, как далеко от центра мы смотрим. Это означает, например, что, глядя на периметр круга с окружностью 2, мы должны найти в два раза больше точек, чем количество точек на периметре круга с окружностью 1.

С длины окружности (2πr) растет линейно с r, из этого следует, что количество случайных точек должно линейно расти с r. Другими словами, желаемое функция плотности вероятности (PDF) растет линейно. Поскольку PDF должен иметь площадь равную 1, а максимальный радиус равен 1, то есть

таким образом, мы знаем, как должна выглядеть желаемая плотность наших случайных значений. Теперь:как мы генерируем такое случайное значение, когда все мы имеют равномерное случайное значение между 0 и 1?

1. из PDF создайте кумулятивная функция распределения (CDF)
2. зеркало это вдоль y = x
3. применить полученную функцию к равномерному значению от 0 до 1.

звучит сложно? Позвольте мне вставить желтую коробку с небольшим количеством боковой путь, который передает интуицию:

Предположим, мы хотим создать случайную точку со следующим распределением:

• 1/5 из пунктов равномерно между 1 и 2, и
• 4/5 точек равномерно между 2 и 3.

CDF, как следует из названия, является накопительной версией PDF. Интуитивно: Пока PDF (x) описывает количество случайных значений на x, CDF (x) описывает количество случайных значений меньше, чем x.

в этом случае CDF будет выглядеть так:

чтобы увидеть, как это полезно, представим, что мы стреляем пулями слева направо на равномерно распределенных высот. Когда пули попадают в линию, они падают на землю:—10—>

посмотрите, как плотность пуль на земле соответствует нашему желаемому распределению! Мы почти на месте!

проблема в том, что для этой функции y ось —выход и x ось —вход. Мы можем только «стрелять пулями с земли прямо вверх»! Нам нужна обратная функция!

вот почему мы отражаем все это; x становится y и y становится x:

мы называем это CDF -1 . Чтобы получить значения в соответствии с желаемым распределением, мы используем CDF -1 (random ()).

. Итак, вернемся к генерации случайных значений радиуса, где наш PDF равен 2x.

Шаг 1: Создайте CDF:

Поскольку мы работаем с reals, CDF выражается как Интеграл PDF.

Шаг 2: Зеркало CDF вдоль y = x:

математически это сводится к замене x и y и решения для y:

Шаг 3: примените полученную функцию к равномерному значению между 0 и 1

CDF -1 (random ()) = √random ()

что мы намеревались вывести: -)

вот быстрое и простое решение.

выбрать два случайных числа в диапазоне (0, 1), а именно a и b . Если b , поменять их местами. Ваша точка зрения (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)) .

вы можете думать об этом решении следующим образом. Если взять круг, вырезать его, а затем выпрямить, получится прямоугольный треугольник. Масштабируйте этот треугольник вниз, и у вас будет треугольник из (0, 0) до (1, 0) to (1, 1) и (0, 0) . Все эти преобразования измените плотность равномерно. То, что вы сделали, — это равномерно выбрать случайную точку в треугольнике и обратить процесс, чтобы получить точку в круге.

обратите внимание на плотность точки пропорционально обратному квадрату радиуса, следовательно, вместо выбора r С [0, r_max] С [0, r_max^2] , затем вычислите свои координаты как:

это даст вам равномерное распределение точек на диске.

подумайте об этом таким образом. Если у вас есть прямоугольник, где одна ось-радиус, а одна-угол, и вы берете точки внутри этого прямоугольника, которые находятся рядом с радиусом 0. Все они будут падать очень близко к началу (то есть близко друг к другу по кругу.) Однако точки вблизи радиуса R все они будут падать вблизи края круга (то есть далеко друг от друга.)

Это может дать вам некоторое представление о том, почему вы получаете такое поведение.

фактор это выведено на этой ссылке говорит вам, сколько соответствующей области в прямоугольнике необходимо настроить, чтобы не зависеть от радиуса, как только он сопоставлен с кругом.

Edit: Итак, то, что он пишет в ссылке, которую вы разделяете, — «это достаточно легко сделать, вычисляя обратное кумулятивное распределение, и мы получаем для r:».

основная предпосылка здесь заключается в том, что вы можете создать переменную с желаемым распределением из равномерного, сопоставив равномерное обратным функция кумулятивной функции распределения желаемой функции плотности вероятности. Почему? Просто примите это как должное, но это факт.

вот мой somehwat интуитивное объяснение математики. Функция плотности f (r) по отношению к r должна быть пропорциональна самой r. Понимание этого факта является частью любой основной книги по исчислению. См. разделы об элементах полярной области. Некоторые другие плакаты упоминали об этом.

поэтому мы назовем его f (r) = C*r;

это, оказывается, большая часть работы. Теперь, поскольку F(r) должна быть плотностью вероятности, вы можете легко увидеть,что, интегрируя f (r) через интервал (0, R), вы получите, что C = 2/R^2 (это упражнение для читателя.)

таким образом, f(r) = 2*r/r^2

OK, так вот как вы получаете формулу в ссылке.

тогда конечная часть идет от равномерной случайной величины u в (0,1), которую вы должны отобразить обратной функцией кумулятивного функция распределения от этой желаемой плотности f (r). Чтобы понять, почему это так, вам нужно найти расширенный текст вероятности, такой как Papoulis, вероятно (или вывести его самостоятельно.)

интегрируя f (r), вы получаете F(r) = r^2/R^2

чтобы найти обратную функцию этого, вы устанавливаете u = r^2 / R^2, а затем решаете для r, что дает вам r = R * sqrt (u)

это полностью имеет смысл интуитивно тоже, u = 0 должно соответствовать r = 0. Кроме того, U = 1 shoudl map to r = R. Также, он идет по функции квадратного корня, которая имеет смысл и соответствует ссылке.

Это действительно зависит от того, что вы подразумеваете под ‘абсолютно случайная’. Это тонкий момент, и вы можете прочитать больше об этом на странице wiki здесь:http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29, где одна и та же проблема, давая разные интерпретации «равномерно случайным» дает разные ответы!

в зависимости от того, как вы выбираете точки, распределение может варьироваться, даже если они равномерно случайны в некоторые чувство.

похоже, что запись в блоге пытается сделать ее равномерно случайной в следующем смысле: если вы берете подпругу круга с тем же центром, то вероятность того, что точка падает в этой области, пропорциональна площади области. Это, я считаю, пытается следовать теперь стандартной интерпретации «равномерно случайных» для 2D-областей с области, определенные на них: вероятность падения точки в любой области (с областью хорошо defined) пропорциональна площади этой области.

причина, по которой наивное решение не работает, заключается в том, что оно дает более высокую плотность вероятности точкам ближе к центру круга. Другими словами, окружность с радиусом r/2 имеет вероятность r/2 получить выбранную в ней точку, но имеет площадь (количество точек) pi*r^2/4.

поэтому мы хотим, чтобы плотность вероятности радиуса имела следующее свойство:

вероятность выбора радиуса меньшего или равного заданному r должна быть пропорциональна площадь окружности с радиусом r. (потому что мы хотим иметь равномерное распределение по точкам, а большие площади означают больше точек)

другими словами, мы хотим, чтобы вероятность выбора радиуса между [0, r] была равна его доле от общей площади круга. Общая площадь окружности равна pi * R^2, а площадь окружности с радиусом r равна pi * r^2. Таким образом,мы хотели бы, чтобы вероятность выбора радиуса между [0, r] была (pi*r^2)/(pi*R^2) = r^2/R^2.

теперь приходит математика:

вероятность выбора радиуса между [0, r] является интегралом от p(r) dr от 0 до r (это просто потому, что мы добавляем все вероятности меньших радиусов). Таким образом, мы хотим Интеграл(p(r)dr) = r^2/R^2. Мы можем ясно видеть, что R^2 является константой, поэтому все, что нам нужно сделать, это выяснить, какой p(r), когда он интегрирован, даст нам что-то вроде r^2. Ответ явно Р * постоянный. Интеграл (R * константа dr) = r^2/2 * константа. Это должно быть равно r^2/R^2, поэтому Константа = 2 / R^2. Таким образом, у вас есть распределение вероятностей p(r) = r * 2/R^2

Примечание:

вот мой код Python для генерации num случайные точки из окружности радиуса rad :

пусть ρ (радиус) и φ (Азимут) — две случайные величины, соответствующие полярным координатам произвольной точки внутри круга. Если точки распределены равномерно, то какова функция распределения ρ и φ?

где S1 и S0-площади круга радиус r и R соответственно. Таким образом, CDF можно дать как:

обратите внимание, что для r=1 случайная величина sqrt(X), где X равномерна на [0, 1), имеет этот точный CDF (потому что P[sqrt(X)

распределение φ, очевидно, равномерно от 0 до 2*π. Теперь вы можете создавать случайные полярные координаты и преобразовывать их в Декартовые, используя тригонометрические уравнения:

не могу сопротивляться сообщение кода python для R=1.

вы получите

Видео:Алгоритмы. Пересечение окружностейСкачать

Создайте случайную точку внутри круга (равномерно)

Мне нужно создать равномерно случайную точку в круге радиуса R.

Я понимаю, что, просто выбирая равномерно случайный угол в интервале [0. 2π) и равномерно случайный радиус в интервале (0. R), я получаю больше точек к центру, так как для двух заданных радиусы, точки меньшего радиуса будут ближе друг к другу, чем точки большего радиуса.

Я нашел запись в блоге по этому поводу здесь, но я не понимаю его рассуждения. Я полагаю, что это правильно, но я бы очень хотел понять, откуда он (2/R 2 ) × r, и как он получает окончательное решение.

Обновление: через 7 лет после публикации этого вопроса я до сих пор не получил удовлетворительного ответа на фактический вопрос относительно математики за алгоритмом квадратного корня. Поэтому я потратил целый день на письменный ответ. Ссылка на мой ответ.

Видео:Уроки Python #9 | Случайные числа | RANDOMСкачать

ОТВЕТЫ

Ответ 1

Видео:# Введение в Python 3 | Урок 7 | Генератор случайных чисел random |Скачать

Как сгенерировать случайную точку внутри круга радиуса R:

(Предполагая, что random() дает значение от 0 до 1 равномерно)

Если вы хотите преобразовать это в декартовы координаты, вы можете сделать

Видео:Функции trunc, floor, ceil. Округление вверх и вниз в pythonСкачать

Почему sqrt(random()) ?

Давайте посмотрим на математику, которая приводит к sqrt(random()) . Предположим для простоты, что мы работаем с единичным кругом, т.е. R = 1.

Среднее расстояние между точками должно быть одинаковым независимо от того, как далеко от центра мы смотрим. Это означает, например, что, глядя на периметр окружности с окружностью 2, мы должны найти вдвое больше точек, чем количество точек на периметре окружности с окружностью 1.

Поскольку окружность окружности (2π r) растет линейно с ростом r, отсюда следует, что число случайных точек должно расти линейно с ростом r. Другими словами, искомая функция плотности вероятности (PDF) растет линейно. Так как PDF должен иметь площадь, равную 1, а максимальный радиус равен 1, мы имеем

Итак, мы знаем, как должна выглядеть желаемая плотность наших случайных значений. Теперь: как мы генерируем такое случайное значение, когда все, что у нас есть, это равномерное случайное значение между 0 и 1?

1. Из PDF создайте накопительную функцию распределения (CDF)
2. Отразите это вдоль y = x
3. Примените полученную функцию к равномерному значению от 0 до 1.

Звучит сложно? Позвольте мне вставить желтое поле с небольшим боковым отступом, которое передает интуицию:

Предположим, мы хотим создать случайную точку со следующим распределением:

• 1/5 баллов равномерно между 1 и 2, и
• 4/5 баллов равномерно между 2 и 3.

CDF — это, как следует из названия, кумулятивная версия PDF. Интуитивно понятно: в то время как PDF (x) описывает количество случайных значений в точке x, CDF (x) описывает количество случайных значений меньше значения x.

В этом случае CDF будет выглядеть так:

Чтобы увидеть, как это полезно, представьте, что мы стреляем пулями слева направо на равномерно распределенных высотах. Когда пули попадают в линию, они падают на землю:

Посмотрите, как плотность пуль на земле соответствует нашему желаемому распределению! Мы почти там!

Проблема в том, что для этой функции ось y является выходной, а ось x является входной. Мы можем только «стрелять пулями прямо с земли»! Нам нужна обратная функция!

Вот почему мы отражаем все это; х становится у, а у становится х:

Мы называем это CDF -1 . Чтобы получить значения в соответствии с желаемым распределением, мы используем CDF -1 (random()).

… Итак, вернемся к генерации случайных значений радиуса, где наш PDF равен 2 х.

Шаг 1: Создайте CDF:

Поскольку мы работаем с реалами, CDF выражается как интеграл PDF.

Шаг 2: Зеркально отразите CDF вдоль y = x:

Математически это сводится к обмену x и y и решению для y:

Шаг 3: применить полученную функцию к равномерному значению от 0 до 1

CDF -1 (random()) = √random()

Что мы и собираемся извлечь 🙂

Ответ 2

Подходим к этому, как это сделал Архимед.

Как мы можем генерировать точку равномерно в треугольнике ABC, где | AB | = | BC |? Позвольте сделать это проще, перейдя к параллелограмму ABCD. Легко создавать точки равномерно в ABCD. Мы равномерно выбираем случайную точку X на AB и Y на BC и выбираем Z такой, что XBYZ является параллелограммом. Чтобы получить равномерно выбранную точку в исходном треугольнике, мы просто складываем любые точки, которые появляются в ADC, обратно вниз до ABC вдоль AC.

Теперь рассмотрим круг. В пределе мы можем рассматривать это как бесконечное множество изоцелевых треугольников ABC с B в начале координат и A и C на окружности, исчезающе близкой друг к другу. Мы можем выбрать один из этих треугольников, просто выбрав угол тета. Поэтому нам нужно создать расстояние от центра, выбрав точку в ABC. Опять же, переходим к ABCD, где D теперь вдвое больше радиуса от центра окружности.

Выбор случайной точки в ABCD легко с использованием вышеуказанного метода. Выберите случайную точку на AB. Равномерно выберите случайную точку на ВС. То есть. выберем пару случайных чисел х и у равномерно на [0, R], давая расстояния от центра. Наш треугольник — тонкая лента, так что AB и BC по существу параллельны. Таким образом, точка Z является просто расстоянием x + y от начала координат. Если x + y > R отбрасываем назад.

Здесь полный алгоритм для R = 1. Надеюсь, вы согласитесь на это довольно просто. Он использует триггер, но вы можете дать гарантию того, сколько времени потребуется, и сколько ему нужно random() , в отличие от выборки отбраковки.

Здесь он находится в Mathematica.

Ответ 3

Вот быстрое и простое решение.

Выберите два случайных числа в диапазоне (0, 1), а именно a и b . Если b , замените их. Ваша точка (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)) .

Вы можете подумать об этом решении следующим образом. Если бы вы взяли круг, разрезали его, а затем выпрямили, вы получили прямоугольный треугольник. Масштабируйте треугольник вниз, и у вас будет треугольник от (0, 0) до (1, 0) до (1, 1) и обратно до (0, 0) . Все эти преобразования меняют плотность равномерно. То, что вы сделали, равномерно выбрали случайную точку в треугольнике и изменило процесс, чтобы получить точку в круге.

Ответ 4

Обратите внимание на плотность точек пропорционально обратному квадрату радиуса, поэтому вместо того, чтобы выбирать r из [0, r_max] , выберите из [0, r_max^2] , затем вычислите свои координаты как:

Это даст вам равномерное распределение точек на диске.

Ответ 5

Подумайте об этом так. Если у вас есть прямоугольник, где одна ось равна радиусу, а одна — углу, и вы берете точки внутри этого прямоугольника, близкие к радиусу 0. Все они будут очень близки к началу координат (это близко к кругу). Однако, точки вблизи радиуса R, все они будут падать рядом с краем круга (то есть далеко друг от друга).

Это может дать вам некоторое представление о том, почему вы получаете такое поведение.

Коэффициент, полученный на этой ссылке, указывает вам, насколько соответствующая область в прямоугольнике должна быть скорректирована так, чтобы не зависеть от радиуса, когда она была сопоставлена ​​с кругом.

Изменить: Итак, что он пишет в ссылке, которую вы разделяете: «Это достаточно легко сделать, вычисляя обратное кумулятивное распределение, и мы получаем для r:».

Основная предпосылка заключается в том, что вы можете создать переменную с желаемым распределением из равномерной путем сопоставления равномерной обратной функцией кумулятивной функции распределения желаемой функции плотности вероятности. Зачем? Просто возьмите это как должное, но это факт.

Вот мое немного интуитивное объяснение математики. Функция плотности f (r) по r должна быть пропорциональна самой r. Понимание этого факта является частью любых базовых книг по исчислению. См. Разделы о полярных элементах. Некоторые другие плакаты упомянули об этом.

Итак, будем называть его f (r) = C * r;

Это, как оказалось, большая часть работы. Теперь, так как f (r) должна быть плотностью вероятности, нетрудно видеть, что интегрируя f (r) на интервале (0, R), вы получаете, что C = 2/R ^ 2 (это упражнение для читателя.)

Таким образом, f (r) = 2 * r/R ^ 2

ОК, так как вы получите формулу в ссылке.

Тогда конечная часть идет от равномерной случайной величины u в (0,1), которую вы должны отобразить обратной функцией кумулятивной функции распределения из этой требуемой плотности f (r). Чтобы понять, почему это так, вам нужно найти расширенный текст вероятности, например, Папулис (или получить его самостоятельно).

Интегрируя f (r), вы получаете F (r) = r ^ 2/R ^ 2

Чтобы найти обратную функцию этого, вы задаете u = r ^ 2/R ^ 2, а затем решим для r, что дает вам r = R * sqrt (u)

Это тоже имеет смысл интуитивно, u = 0 следует отображать в r = 0. Кроме того, u = 1 shoudl map to r = R. Кроме того, это функция квадратного корня, которая имеет смысл и соответствует ссылке.

Ответ 6

Причина, по которой наивное решение не работает, заключается в том, что она дает более высокую плотность вероятности точкам, расположенным ближе к центру окружности. Другими словами, круг с радиусом r/2 имеет вероятность r/2 получения выбранной в нем точки, но имеет площадь (количество точек) pi * r ^ 2/4.

Поэтому мы хотим, чтобы плотность вероятности радиуса имела следующее свойство:

Вероятность выбора радиуса, меньшего или равного заданному r, должна быть пропорциональна площади окружности с радиусом r. (потому что мы хотим иметь равномерное распределение по точкам, а большие области — больше очков)

Другими словами, мы хотим, чтобы вероятность выбора радиуса между [0, r] была равна его доле общей площади круга. Общая площадь окружности равна pi * R ^ 2, а площадь круга с радиусом r равна pi * r ^ 2. Таким образом, мы хотели бы, чтобы вероятность выбора радиуса между [0, r] была (pi * r ^ 2)/(pi * R ^ 2) = r ^ 2/R ^ 2.

Теперь идет математика:

Вероятность выбора радиуса между [0, r] является интегралом от p (r) dr от 0 до r (это только потому, что мы добавляем все вероятности меньших радиусов). Таким образом, мы хотим, чтобы интеграл (p (r) dr) = r ^ 2/R ^ 2. Мы можем ясно видеть, что R ^ 2 является константой, поэтому нам нужно всего лишь выяснить, какая из p (r), когда интегрированная даст нам нечто вроде r ^ 2. Ответ явно r * постоянный. интеграл (r * const dr) = r ^ 2/2 * постоянный. Это должно быть равно r ^ 2/R ^ 2, поэтому константа = 2/R ^ 2. Таким образом, у вас есть распределение вероятности p (r) = r * 2/R ^ 2

Примечание. Еще один интуитивный способ подумать о проблеме состоит в том, чтобы представить, что вы пытаетесь дать каждой окружности радиуса вероятности вероятности равную пропорции количества очков, которые она имеет на своем длина окружности. Таким образом, окружность с радиусом r будет иметь 2 * pi * r «точки» по ее окружности. Общее число точек pi * R ^ 2. Таким образом, вы должны дать окружности r вероятность, равную (2 * pi * r)/(pi * R ^ 2) = 2 * r/R ^ 2. Это намного легче понять и более интуитивно понятным, но это не так, как математически здорово.

Ответ 7

Это действительно зависит от того, что вы подразумеваете под «равномерно случайным». Это тонкая точка, и вы можете прочитать больше об этом на странице wiki здесь: http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29, где та же проблема, дающая разные интерпретации «равномерно случайный» дает разные ответы!

В зависимости от того, как вы выбираете точки, распределение может меняться, хотя они в какой-то мере равномерны.

Кажется, что запись в блоге пытается сделать его равномерным случайным в следующем смысле: если вы возьмете субкруг круга с тем же центром, то вероятность того, что точка попадет в эту область, пропорциональна области региона. Это, я считаю, пытается следовать теперь стандартной интерпретации «равномерно случайных» для 2D-областей с областями, определенными на них: вероятность точки падение в любой области (с четко определенной областью) пропорционально площади этой области.

Ответ 8

Пусть ρ (радиус) и φ (азимут) две случайные величины, соответствующие полярным координатам произвольной точки внутри окружности. Если точки распределены равномерно, то какова функция распределения ρ и φ?

Для любого r: 0 2

Где S1 и S0 — площади круга радиуса r и R соответственно. Таким образом, CDF может быть дан как:

Обратите внимание, что для R = 1 случайная величина sqrt (X), где X равномерно на [0, 1), имеет этот точный CDF (потому что P [sqrt (X)

Ответ 9

Вот мой код Python для генерации num случайных точек из круга радиуса rad :

Ответ 10

Я думаю, что в этом случае использование полярных координат является способом усложнения задачи, было бы намного проще выбрать случайные точки в квадрат со сторонами длины 2R и затем выбрать точки (x,y) такие, что x^2+y^2 .

Ответ 11

Решение в Java и пример распространения (2000 точек)

на основе решения previum fooobar.com/questions/41617/. из @sigfpe

Ответ 12

Сначала мы сгенерируем cdf [x], который является

Вероятность того, что точка меньше расстояния x от центра круга. Предположим, что окружность имеет радиус R.

очевидно, если x равно нулю, то cdf [0] = 0

очевидно, если x равно R, то cdf [R] = 1

очевидно, если x = r, то cdf [r] = (Pi r ^ 2)/(Pi R ^ 2)

Это связано с тем, что каждая «небольшая область» на круге имеет такую ​​же вероятность быть выбрана, поэтому вероятность пропорциональна этой области. А площадь, заданная на расстоянии x от центра круга, равна Pi r ^ 2

поэтому cdf [x] = x ^ 2/R ^ 2, потому что Pi отменяют друг друга

имеем cdf [x] = x ^ 2/R ^ 2, где x переходит от 0 в R

Итак, мы решаем для x

Теперь мы можем заменить cdf на случайное число от 0 до 1

получаем полярные координаты

Ответ 13

Существует линейная зависимость между радиусом и числом точек «около» этого радиуса, поэтому ему необходимо использовать распределение радиуса, которое также делает число точек данных вблизи радиуса r пропорциональным r .

Ответ 14

Элемент области в круге равен dA = rdr * dphi. Этот дополнительный фактор разрушил вашу идею, чтобы случайным образом выбрать r и phi. В то время как phi распределена плоской, r не является, а плоской в ​​1/r (то есть вы с большей вероятностью попадете на границу, чем «бычий глаз» ).

Итак, чтобы создать точки, равномерно распределенные по кругу, выбрать phi из плоского распределения и r из распределения 1/r.

В качестве альтернативы можно использовать метод Монте-Карло, предложенный Мехрдадом.

ИЗМЕНИТЬ

Чтобы выбрать случайную r плоскую в 1/r, вы можете выбрать случайный x из интервала [1/R, бесконечность] и вычислить r = 1/x. r затем распределяется плотно в 1/r.

Чтобы вычислить случайный phi, выберите случайный x из интервала [0, 1] и вычислим phi = 2 * pi * x.

Ответ 15

Я использовал этот метод: Это может быть совершенно неоптимизировано (т.е. Использует массив точек, поэтому он непригоден для больших кругов), но дает случайное распределение. Вы можете пропустить создание матрицы и нарисовать напрямую, если хотите. Метод состоит в том, чтобы рандомизировать все точки в прямоугольнике, которые попадают внутрь круга.

Ответ 16

Я не знаю, открыт ли этот вопрос для нового решения со всем ответом, который уже был дан, но я столкнулся с одним и тем же вопросом. Я попытался «разгадать» себя для решения, и нашел его. Это может быть то же самое, что некоторые из них уже предложены здесь, но в любом случае это:

для того, чтобы два элемента поверхности окружности были равны, если принять равные dr, мы должны иметь dtheta1/dtheta2 = r2/r1. Написание выражения вероятности для этого элемента как P (r, theta) = P

Ответ 17

Решение для программистов:

• Создайте битовую карту (матрицу логических значений). Он может быть как можно большим.
• Нарисуйте круг в этой битовой карте.
• Создайте таблицу поиска точек окружности.
• Выберите случайный индекс в этой таблице поиска.

Растровое изображение необходимо только для объяснения логики. Это код без растрового изображения:

Ответ 18

Я все еще не уверен в точном ‘(2/R2) × r’, но очевидно, что количество точек, которые необходимо распределить в данной единице ‘dr’, то есть увеличение r будет пропорционально r2, а не р.

проверьте этот путь. число точек под некоторым углом tta и между r (0.1r до 0.2r), то есть доля r и количество точек между r (0.6r to 0.7r) будут равны, если вы используете стандартная генерация, так как разница составляет всего 0,1r между двумя интервалами. но поскольку площадь, покрываемая между точками (0.6r до 0.7r), будет намного больше, чем площадь, лежащая между 0.1r до 0.2r, равное количество точек будет рассеянно разнесено в большей области, это я предполагаю, что вы уже знаете, поэтому функция для генерации случайных точек не должно быть линейным, но квадратичным (так как число точек, требуемых для распределения в данной единице «dr», то есть увеличение r будет пропорционально r2, а не r), поэтому в этом случае оно будет обратным квадратично, так как дельта у нас (0.1r) в обоих интервалах должна быть квадратной некоторой функции, поэтому она может действовать как начальное значение для линейной генерации точек (так как послесловие это семя используется линейно по функции sin и cos), поэтому мы знаете, dr должно быть квадратичным значением и сделать это семена квадратичным, нам нужно вывести эти значения из квадратного корня из r не r, я надеюсь, что это делает его более понятным.

Ответ 19

Такая забавная проблема.
Объяснение вероятности того, что выбранная точка опускается как расстояние от начала оси, объясняется несколько раз выше. Мы учитываем это, беря корень из U [0,1]. Здесь общее решение для положительного r в Python 3.

Ответ 20

Вы также можете использовать свою интуицию.

Площадь круга равна pi*r^2

Это дает нам область pi . Предположим, что мы имеем некоторую функцию f , которая равномерно распределяла бы N=10 точек внутри круга. Соотношение здесь 10/pi

Теперь мы удваиваем площадь и количество точек

Это дает площадь 4pi и теперь соотношение составляет 20/4pi или 10/2pi . Отношение будет становиться все меньше и меньше, чем больше радиус, так как его рост квадратичен, а N линейно.

Чтобы исправить это, мы можем просто сказать

Если вы создадите вектор в полярных координатах, как это

Больше очков приземлится вокруг центра.

length уже не равномерно распределена, но теперь вектор будет равномерно распределен.

Ответ 21

1) Выберите случайный X между -1 и 1.

2) Используя формулу окружности, вычислим максимальное и минимальное значения Y, учитывая, что X и радиус 1:

3) Выберите случайный Y между этими крайностями:

4) Включите ваши значения местоположения и радиуса в конечном значении:

📸 Видео

Алгоритмы. Попадание точки в треугольникСкачать

Python #5 Обработка вещественных чисел. Случайные числаСкачать

Вычисление площади круга и длинны окружности по заданному радиусу в Паскаль с применением константыСкачать

Как задать случайный цвет turtle | Программирование на PythonСкачать

Персептрон - возможности классификации образов, задача XOR | #2 нейросети на PythonСкачать

Алгоритмы на Python 3. Лекция №4Скачать

Модули и классы в языке Python. Точки и координаты на плоскости.Скачать

Питон за 60 секунд! Факты о числах с плавающей точкой в Python #shorts #pythonСкачать

Поиск пары ближайших точек | Скринкасты | MADE Академия данных |#3Скачать

Точность и ошибки округления в Python | Функция round и тип данных float (дробные числа)Скачать