Сколько треугольников в окружности

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

• Главная 
• Вопросы & Ответы 
• Вопрос 1865017

Главный Попко

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сколько треугольников в окружности? пж срочно кушать хочу

Видео:Равносторонний треугольник в окружностиСкачать

Треугольник вписанный в окружность

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

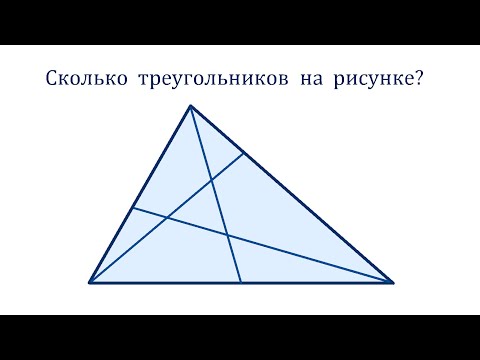
Видео:Сколько треугольников на рисунке? Универсальный алгоритм решения задачиСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Сколько треугольников на картинке? Расскажу, как посчитать это за 7 секунд!Скачать

Задача про круги: кажется сложной, но она очень простая!

Раздумывая над решением, не спешите сдаваться. Все гораздо легче, чем вам может показаться на первый взгляд. И пусть здесь нет программирования, зато есть возможность развивать логическое мышление.

Условие: даны три одинаковых соприкасающихся круга диаметром 1 м. Их опоясывает эластичная лента.

Задание: найдите длину ленты, натянутой вокруг кругов.

Для того чтобы найти ответ, вам не нужны сложные формулы, такие как расчет кривизны и т.п. На самом деле все гораздо проще.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Строим треугольник

Для начала соединим центры кругов таким образом, чтобы получился треугольник.

По законам геометрии, центры соприкасающихся кругов можно соединить прямой линией, причем точка касания будет находиться именно на ней. Так как диаметр равен 1 метру, радиусы всех кругов равны 0,5 метра. Укажем это на схеме:

Выходит, что стороны треугольника равны между собой и длина каждой из них составляет 0,5 + 0,5 = 1. Зафиксируем это и двигаемся дальше.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Создаем проекцию

Все вершины треугольника соединим с лентой линиями, проведенными под углом 90°.

Получились прямоугольники. Как известно, противоположные стороны этой фигуры равны, а раз длина каждой стороны треугольника равна 1, данные отрезки ленты также равны 1:

Теперь нужно найти длину трех оставшихся секций:

Видео:СКОЛЬКО ТРЕУГОЛЬНИКОВ? 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Находим длину секций

В круге 360 градусов. Треугольник, который мы построили из центров кругов, равносторонний. Следовательно, каждый угол в нем равен 60°. У прямоугольников углы по 90°. Обозначим все это на схеме:

Находим неизвестный угол:

90 + 60 + 90 + X = 360

120° — это ровно одна третья часть круга, а мы имеем 3 таких части:

Получается, что все вместе они формируют один полный круг. Нам известно, что радиус данного круга равен 0,5, а диаметр – 1. Это позволяет вычислить длину окружности:

Прибавляем к этому числу длины 3-х отрезков и получаем длину всей ленты: 3 + π.

💥 Видео

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Сколько треугольников на рисунке? Простая задача, которая позволяет загрузить даже студентовСкачать

Сколько треугольников на рисунке?Скачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Сколько треугольников вы видите на рисункеСкачать

Сколько треугольников?Скачать

Сколько треугольников на картинке?Скачать

Способ сосчитать треугольники, которому не учат в школе! Сколько треугольников на картинке?Скачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

Центр кругаСкачать