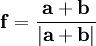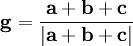Сфера из треугольников развертка

Развертка сферы на плоскость. Калькулятор вычисляет основные параметры развертки, а также выводит координаты точек для построения развертки одной доли.

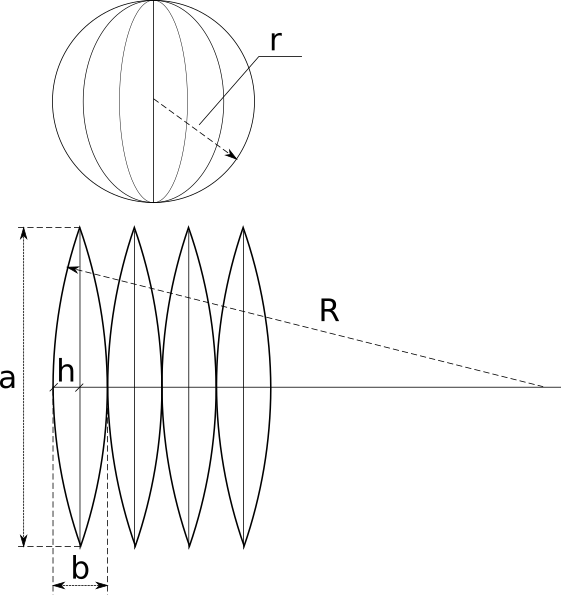
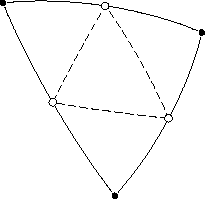
Калькулятор рассчитывает параметры развертки сферы на плоскости. Картинка ниже иллюстрирует задачу.

Итак, нам известен радиус сферы r и число долей на которое мы хотим ее разбить n. Для описания развертки нам надо найти высоту «дольки» a, ширину «дольки» b, и радиус R большой дуги, на которой построена «долька». Формулы расчета и объяснения, как обычно, приведены под калькулятором.

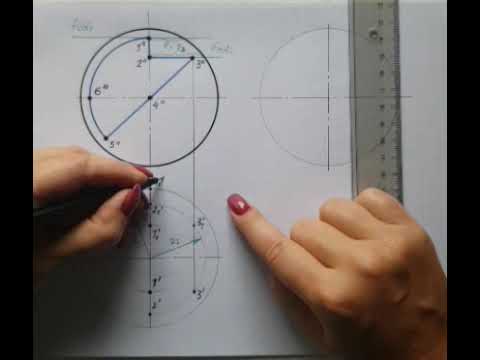
Развертка сферы

С высотой все понятно — это половина длины окружности, которую можно получить при сечении сферы плоскостью, проходящей через центр. Таким образом,
.
С шириной тоже все понятно — это часть той же окружности, полученная при разбиении всей окружности на n частей:

Радиус дуги можно вычислить по длине хорды (это а) и высоте сегмента (это h=b/2) по следующей формуле (см. Сегмент круга).

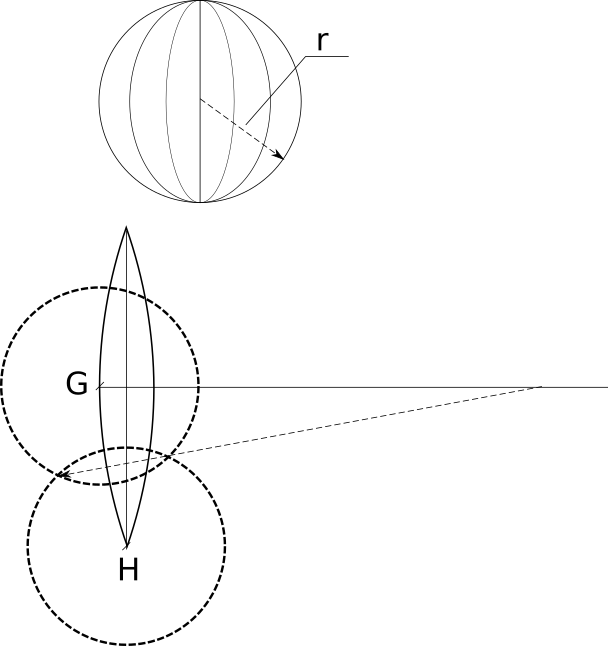
В принципе, найдя a и b, считать радиус R даже не обязательно — его можно найти по построению, что иллюстрирует следующая картинка.

Для нахождения радиуса из точек G и H надо провести две окружности, так, чтобы они пересекались — прямая, проведенная через точки пересечения, пересечет среднюю линию в точке центра окружности, на дуге которой лежат G и H.

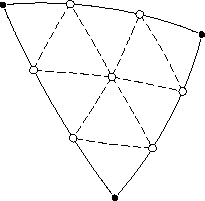
Несмотря на всю простоту, у метода есть один недостаток — а именно, ему нужно очень много места сбоку для радиуса, и чем больше число долек, на которое мы хотим разбить сферу, тем больше радиус большой дуги. Не везде будет возможность найти столько места и такой большой «циркуль», чтобы нарисовать дугу. Поэтому калькулятор, кроме расчета параметров «дольки», также рассчитывает координаты точек, лежащих на дуге — можно строить дуги дольки по точкам, не используя радиус. Для того, чтобы рассчитать координаты точек, надо пометить флажок «Сгенерировать точки развертки», и указать число точек — дуга будет разбита на заданное число точек с равным угловым шагом, как показано на рисунке:

Видео:FreeCad Сфера из треугольниковСкачать

Геодезический купол. Об устройстве и моем опыте расчетов

Пожалуй сложно назвать геодезические купола чем-то необычным или новым. В этой заметке я расскажу немного об этих конструкциях в общем, об их устройстве, а также покажу на примере как я кое что на эту тему считал. Код тоже будет.

Википедию цитировать не буду. Почему я выбрал купол в качестве дома?

• При равном объеме площадь поверхности сферы будет меньше, чем у любой другой формы. Это положительно влияет как на материалоемкость, так и на энергозатраты при эксплуатации.
• Мне нравится как выглядит сфера.
• Это интересный инженерный проект, в каком-то смысле даже вызов. Это сложно, трудно и потому весело!

Как это геодезические сферы устроены вообще? С первого взгляда кажется, что это какое-то переплетение рёбер и уловить систему сложно. В этой заметке попробуем разобраться.

В основе таких конструкций лежит икосаэдр или октаэдр. В общем правильный многогранник.
В моем случае это был именно икосаэдр и чаще используют его. Далее берем одну грань и заменяем ее на несколько треугольников, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра. Звучит не слишком складно. Отвлечемся.

Есть замечательный калькулятор www.acidome.ru который позволяет в реальном времени покрутить геодезик. Берем в качестве основы icosahedron, ставим частоту 1, часть сферы 1/1.

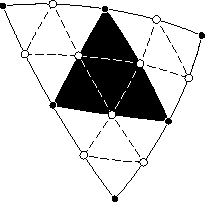
Это и есть наш основной икосаэдр. Частота это на сколько частей мы разобьем каждое ребро икосаэдра. Ставим 3,4, 5 и ничего становится непонятно. Переключаем в режим кровли и ищем пятиугольники. В тех местах, где у нас вершина икосаэдра — будет пятиугольник. Между тремя пятиугольниками грань икосаэдра.

Если внимательно смотреть на геодезик и знать, что искать (обычно пятиугольник), то становится видна регулярность структуры. На Биосфере в Монреале при должном усердии можно найти пятиугольники и посчитать частоту. Частота у нас равна количеству ребер между двумя пятиугольниками.

Сами “большие” треугольники, с вершинами на вершинах икосаэдра также имеют структуру. На acidome в режиме кровли это видно по цвету. Треугольники расположены симметрично относительно центра “большого” треугольника. Количество их типов меньше общего числа треугольников. В случае с частотой 5 уникальных треугольников 9.

В процессе проектирования дома я столкнулся с задачей постройки сферы в Dynamo. Это такой инструмент, который позволяет научить Autodesk Revit работать со сложными формами. Такая среда визуального программирования.
Погуглив я даже нашел скетч, который в Dynamo строил геодезическую сферу. Сферу то он строил, да не ту.

Дело вот в чем. Когда мы берем одно ребро икосаэдра и делим его на мелкие треугольники — сделать это можно несколькими способами. В acidome за это отвечает переключатель “метод разбиения”.

Найденный скетч строил сферу методом равных хорд. Что это значит? Мы берем большой треугольник икосаэдра, каждое его ребро делим на нужное нам количество частей, соединяем точки на ребрах между собой и получаем плоскую сетку из треугольников. Затем эту сетку мы проецируем на сферу. Все бы хорошо, но сами эти треугольники достаточно сильно отличаются по размеру. Центральный больше всех. Оно и понятно, центр “большого” треугольника у нас на максимальном расстоянии от сферы. Это плохо, так как в этом случае сложнее оптимизировать расход материалов. Будет больше отходов.

Другой метод разбиения (равными дугами) предполагает, что мы строим поверх “большого” треугольника дуги и уже их делим на равные части. Подход отличается, простой проекцией не обойтись.

Скетч не подходил. Я попытался его исправить и в итоге мне пришлось нырнуть в это дело с головой.

Как оказалось помимо визуальной среды Dynamo имеет встроенный Python. С этим языком я ранее не сталкивался, но где наша не пропадала? В конце концов это просто инструмент.

Дальше будут кусочки кода, прошу обратить внимание, что это мой hello world в python, а целью было не построить максимально эффективное и производительное решение, а построить нужную сферу.

Метод равных дуг.

Берем одну из граней икосаэдра и из углов этого треугольника строим дуги.

Затем дуги делим на равные части и соединяем точки на дугах новыми дугами. У всех дуг один центр — центр сферы. Точки соединяем не все со всеми, а одноименные. На картинке оно выглядит попроще, чем в коде.

Опа, а дуги то не пересекаются! Не слишком беглое гугление вывело меня на книгу, которая подтвердила мои предположения о том, что нужно в качестве вершины ребра геодезика использовать центр треугольника, образованного пересечением дуг. Также курил исходники acidome, но не помню нашел ли там этому подтверждение. Помню, что было интересно.
Центры надо как-то найти. Это центр треугольника и это не сложно, но нужно было понять где же у нас в ворохе точек эти треугольники. Мне показалось самым простым вариантом соединять ближайшие друг к другу точки.

Теперь нам нужно соединить между собой собранные на разных этапах точки, которые и являются вершинами ребер геодезической сферы. На картинке эти точки видно хорошо, но вот когда они в массиве — все сложнее. Было несколько вариантов, но так как задача была с наименьшими трудозатратами получить рабочий скрипт, вышло вот это:

Сегмент готов. Наверное существует какой-то правильный путь для решения этой задачи, но я проложил свой.

Дальше сегмент разворачивается, несколько раз копируется копируется и получается полная сфера. Вот один из поворотов:

Скриптик вышел страшненький, я его пару раз переписывал, так как были проблемы с экспортом в Revit. Думал, что проблемы с построением. В итоге на форуме Dynamo индус подсказал украинцу и все удалось!

Теперь можно строить сферу любой частоты и любого диаметра. Сравнение размеров с результатами acidome показало, что все сходится с высокой точностью. Повторяемость это хорошо.

Также я занялся оптимизацией размеров с целью минимизации обрезков. Так как все размеры были у меня на руках это было не так трудно. В итоге радиус сферы получился 5,65 метров при частоте 5. Такие размеры позволяют мне достаточно эффективно использовать материалы шириной 125 см. Такую ширину имеют листы OSB, листового металла, утеплителя, гипсокартона. При хорошей оптимизации количество обрезков минимально. Наилучших результатов можно добиться путем расчета раскладок треугольников на материале, но этим я не занимался.

Дальше было проще, так как Revit съел сложную форму и позволил с ней работать примерно с тем же успехом, что и с квадратно-параллельной.

Конечно, трудности на этом не закончились, но это уже совсем другая история.

Видео:Построение недостающих проекции сквозного отверстия в сфереСкачать

Сфера из треугольников вектор

Видео:развертка сферыСкачать

Геодезический купол. Об устройстве и моем опыте расчетов

Пожалуй сложно назвать геодезические купола чем-то необычным или новым. В этой заметке я расскажу немного об этих конструкциях в общем, об их устройстве, а также покажу на примере как я кое что на эту тему считал. Код тоже будет.

Википедию цитировать не буду. Почему я выбрал купол в качестве дома?

• При равном объеме площадь поверхности сферы будет меньше, чем у любой другой формы. Это положительно влияет как на материалоемкость, так и на энергозатраты при эксплуатации.
• Мне нравится как выглядит сфера.
• Это интересный инженерный проект, в каком-то смысле даже вызов. Это сложно, трудно и потому весело!

Как это геодезические сферы устроены вообще? С первого взгляда кажется, что это какое-то переплетение рёбер и уловить систему сложно. В этой заметке попробуем разобраться.

В основе таких конструкций лежит икосаэдр или октаэдр. В общем правильный многогранник.
В моем случае это был именно икосаэдр и чаще используют его. Далее берем одну грань и заменяем ее на несколько треугольников, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра. Звучит не слишком складно. Отвлечемся.

Есть замечательный калькулятор www.acidome.ru который позволяет в реальном времени покрутить геодезик. Берем в качестве основы icosahedron, ставим частоту 1, часть сферы 1/1.

Это и есть наш основной икосаэдр. Частота это на сколько частей мы разобьем каждое ребро икосаэдра. Ставим 3,4, 5 и ничего становится непонятно. Переключаем в режим кровли и ищем пятиугольники. В тех местах, где у нас вершина икосаэдра — будет пятиугольник. Между тремя пятиугольниками грань икосаэдра.

Если внимательно смотреть на геодезик и знать, что искать (обычно пятиугольник), то становится видна регулярность структуры. На Биосфере в Монреале при должном усердии можно найти пятиугольники и посчитать частоту. Частота у нас равна количеству ребер между двумя пятиугольниками.

Сами “большие” треугольники, с вершинами на вершинах икосаэдра также имеют структуру. На acidome в режиме кровли это видно по цвету. Треугольники расположены симметрично относительно центра “большого” треугольника. Количество их типов меньше общего числа треугольников. В случае с частотой 5 уникальных треугольников 9.

В процессе проектирования дома я столкнулся с задачей постройки сферы в Dynamo. Это такой инструмент, который позволяет научить Autodesk Revit работать со сложными формами. Такая среда визуального программирования.
Погуглив я даже нашел скетч, который в Dynamo строил геодезическую сферу. Сферу то он строил, да не ту.

Дело вот в чем. Когда мы берем одно ребро икосаэдра и делим его на мелкие треугольники — сделать это можно несколькими способами. В acidome за это отвечает переключатель “метод разбиения”.

Найденный скетч строил сферу методом равных хорд. Что это значит? Мы берем большой треугольник икосаэдра, каждое его ребро делим на нужное нам количество частей, соединяем точки на ребрах между собой и получаем плоскую сетку из треугольников. Затем эту сетку мы проецируем на сферу. Все бы хорошо, но сами эти треугольники достаточно сильно отличаются по размеру. Центральный больше всех. Оно и понятно, центр “большого” треугольника у нас на максимальном расстоянии от сферы. Это плохо, так как в этом случае сложнее оптимизировать расход материалов. Будет больше отходов.

Другой метод разбиения (равными дугами) предполагает, что мы строим поверх “большого” треугольника дуги и уже их делим на равные части. Подход отличается, простой проекцией не обойтись.

Скетч не подходил. Я попытался его исправить и в итоге мне пришлось нырнуть в это дело с головой.

Как оказалось помимо визуальной среды Dynamo имеет встроенный Python. С этим языком я ранее не сталкивался, но где наша не пропадала? В конце концов это просто инструмент.

Дальше будут кусочки кода, прошу обратить внимание, что это мой hello world в python, а целью было не построить максимально эффективное и производительное решение, а построить нужную сферу.

Метод равных дуг.

Берем одну из граней икосаэдра и из углов этого треугольника строим дуги.

Затем дуги делим на равные части и соединяем точки на дугах новыми дугами. У всех дуг один центр — центр сферы. Точки соединяем не все со всеми, а одноименные. На картинке оно выглядит попроще, чем в коде.

Опа, а дуги то не пересекаются! Не слишком беглое гугление вывело меня на книгу, которая подтвердила мои предположения о том, что нужно в качестве вершины ребра геодезика использовать центр треугольника, образованного пересечением дуг. Также курил исходники acidome, но не помню нашел ли там этому подтверждение. Помню, что было интересно.
Центры надо как-то найти. Это центр треугольника и это не сложно, но нужно было понять где же у нас в ворохе точек эти треугольники. Мне показалось самым простым вариантом соединять ближайшие друг к другу точки.

Теперь нам нужно соединить между собой собранные на разных этапах точки, которые и являются вершинами ребер геодезической сферы. На картинке эти точки видно хорошо, но вот когда они в массиве — все сложнее. Было несколько вариантов, но так как задача была с наименьшими трудозатратами получить рабочий скрипт, вышло вот это:

Сегмент готов. Наверное существует какой-то правильный путь для решения этой задачи, но я проложил свой.

Дальше сегмент разворачивается, несколько раз копируется копируется и получается полная сфера. Вот один из поворотов:

Скриптик вышел страшненький, я его пару раз переписывал, так как были проблемы с экспортом в Revit. Думал, что проблемы с построением. В итоге на форуме Dynamo индус подсказал украинцу и все удалось!

Теперь можно строить сферу любой частоты и любого диаметра. Сравнение размеров с результатами acidome показало, что все сходится с высокой точностью. Повторяемость это хорошо.

Также я занялся оптимизацией размеров с целью минимизации обрезков. Так как все размеры были у меня на руках это было не так трудно. В итоге радиус сферы получился 5,65 метров при частоте 5. Такие размеры позволяют мне достаточно эффективно использовать материалы шириной 125 см. Такую ширину имеют листы OSB, листового металла, утеплителя, гипсокартона. При хорошей оптимизации количество обрезков минимально. Наилучших результатов можно добиться путем расчета раскладок треугольников на материале, но этим я не занимался.

Дальше было проще, так как Revit съел сложную форму и позволил с ней работать примерно с тем же успехом, что и с квадратно-параллельной.

Конечно, трудности на этом не закончились, но это уже совсем другая история.

Видео:СФЕРА с вырезомСкачать

GIS-LAB

Географические информационные системы и дистанционное зондирование

Видео:Сфера в SolidWorksСкачать

Создание треугольных сеток на сфере

Рассматриваются вопросы создания треугольной сетки на сфере. Приводится программа построения сетки в сферическом треугольнике на Си. Прилагаются слои сетки на основе икосаэдра.

Видео:Метод эксцентрических сферСкачать

Содержание

Видео:Условная развертка сферы: Начертательная геометрия для архитекторовСкачать

[править] Постановка задачи

Требуется создать регулярное покрытие сферы треугольниками, близкими по размеру и форме. В качестве эталона примем сетку, образованную на плоскости равносторонними треугольниками. Отличие геометрии треугольника от правильной равносторонней будем интерпретировать как искажение формы. [1]

В начале рассмотрим алгоритм построения сетки в базовом сферическом треугольнике. Затем уделим внимание различным способам разделения сферы на базовые сферические треугольники. Наконец, представим пример создания треугольной сетки на основе икосаэдра.

Видео:Развертка пирамидыСкачать

[править] Генерация сетки в сферическом треугольнике

Процедуру создания на некоторой поверхности сетки треугольников обычно называют триангуляцией. В качестве базы для создания сетки используем некоторый сферический треугольник, заданный координатами своих вершин.

[править] Метод бисекции

Назовём бисекцией операцию деления исходного треугольника на четыре треугольника нового поколения. Собственно термин «бисекция» относится к делению сторон пополам. В середины рёбер вставляются новые вершины (белые точки на рисунках), которые соединяются новыми рёбрами (пунктирные линии), образующими новые треугольники. Следующее поколение получается очередной бисекцией.

В терминах геометрии на сфере задача вставки точек в стороны треугольников решается последовательным решением обратной и прямой геодезических задач. Однако в данном случае гораздо проще использовать векторную алгебру. Пусть концы стороны заданы векторами a и b; тогда средняя точка f вычисляется как их нормированная сумма:

[править] Метод трисекции

Исходный треугольник делится на девять треугольников нового поколения. В результате трисекции каждая сторона делится на три равных отрезка, в концы которых вставляются вершины. Итого шесть новых вершин, и седьмая вставляется в геометрический центр треугольника. Вершины соединяются рёбрами, образующими треугольники.

Проще всего вычислить положение центральной точки g:

где a, b и c — векторы вершин исходного треугольника.

Разделить стороны на три равных отрезка сложнее. Удобное решение предлагает утилита PROJ.4 geod:

Здесь параметры lat_1, lon_1, lat_2, lon_2 задают начало и конец линии, а параметр n_S определяет число отрезков. Результатом будут широты и долготы четырёх точек, лежащих на равных расстояниях вдоль линии.

[править] Программная реализация

Приведём пример программы на Си генерации сетки в треугольнике, реализующей метод бисекции:

Текст кода находится в файле triangulate.c в архиве Sph_tri.zip. Файл triangulate.h содержит необходимые объявления:

Создадим исполняемый модуль triangulate компилятором gcc:

Готовый исполняемый модуль для MS Windows triangulate.exe можно найти в архиве Sph_tri-win32.zip.

Программа запускается в командной строке с двумя аргументами. Первый аргумент — название файла, содержащего координаты вершин базового треугольники. Это должен быть текстовый файл, и в первых трёх строках он должен содержать значения координат «долгота широта» в десятичных градусах, разделённые пробелом или табуляцией. Второй аргумент — количество бисекций.

На выходе создаются файлы сетки отдельно для вершин, рёбер и фасеток.

Долготы всех точек в выходных файлах находятся в диапазоне от −180° до +180°.

В качестве координатной системы указана «долгота/широта внутренняя»: "CoordSys Earth Projection 1, 0". MapInfo под нулевым кодом подразумевает WGS 84, но QGIS и, возможно, другие программы интерпретируют этот код неверно. Для использования результатов в программах ГИС следует заменить ноль на требуемый код датума. Так, для WGS 84 следует подставить 104, для сферы Google — 157, а для Pulkovo-42 (Hungary) — 1001. Можно использовать и полную нотацию с явным указанием параметров преобразования Молоденского или Бурша-Вольфа; детали изложены в руководствах пользователя MapInfo Professional.

Видео:Создание развертки сферы - Основы Unwrap UVW | Уроки 3Ds Max для начинающихСкачать

[править] Сферические многогранники

Сферический многогранник — разбиение сферы дугами больших окружностей на замкнутые области, называемые сферическими многоугольниками. Способы разбиения сферы ничем не ограничены. Однако регулярные построения обычно основаны на пространственной симметрии тетраэдра, октаэдра или икосаэдра.

Нас интересуют способы разбиения сферы на равносторонние или близкие к равносторонним треугольники. В центре такого треугольника построенная на его основе сетка будет близка к регулярной. Наибольшие искажения формы сетки будут вблизи углов базового треугольника. Несложный анализ показывает, что с позиции сохранения формы выгоднее всего опираться на симметрию икосаэдра. Подходящие многогранники — правильные и полуправильные, образованные треугольниками либо пяти- и шестиугольниками, которые разбиваются на почти равносторонние треугольники. Рассмотрим лишь несколько многогранников, удовлетворяющих этим требованиям.

Видео:Нахождение точки на развертке сферы: Начертательная геометрия для архитекторовСкачать

Сфера из треугольников вектор

В статье показана триангуляция поверхности вращения и наложение на неё текстуры с помощью метода UV-параметризации. Также есть реализация SkyBox.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Содержание

Видео:SolidWorks развертка поверхности сферыСкачать

Способы рисования сферы

Чтобы аппроксимировать сферу треугольной сеткой, нам потребуется:

• определиться с алгоритмом построения сетки
• вычислить вершины треугольников и атрибуты вершин (например, нормали)
• проиндексировать вершины, составив из них полосу треугольников

Один из способов приближения сферы — это детализация икосаэдра. Среди всех правильных Платоновых тел икосаэдр ближе всего к сфере, кроме того, его грани уже являются треугольниками. Каждая грань может быть разделена на 3 подграни: достаточно составить из этой грани и точки на поверхности сферы тетраэдр, а потом взять три других грани полученного тетраэдра, а изначальную грань отбросить.

Детализация икосаэдра является работоспособным, но слишком сложный способ: нам придётся сначала решать задачу триангуляции икосаэдра, а потом её и задачу детализации граней. Кроме того, такой способ не подходит для любых других тел, кроме сферы. Однако, есть более совершенный метод UV-параметризации, с помощью которого можно нарисовать любое тело вращения.

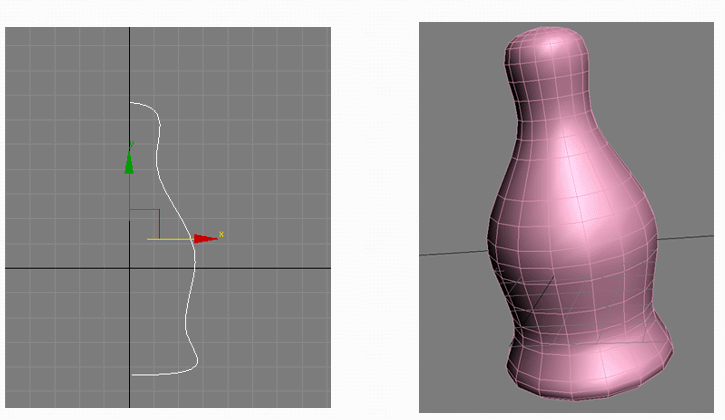
Тела вращения могут быть созданы путём вращения некоторой фигуры, состоящей из кривой и отрезка прямой, вокруг её прямой стороны:

UV параметризация вводит два дополнительных параметра, “u” и “v”. Параметр “u” создаёт деления на “меридиане” тела вращения — то есть на линии, проходящей вдоль оси вращения тела. Параметр “v” создаёт деления на “параллели”, то есть на линии, оборачивающей тело вращения подобно экватору или параллели глобуса.

Видео:Построение развертки тела вращенияСкачать

UV-параметризация сферы

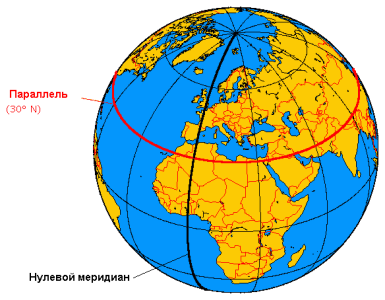
В географии принято разделять глобус двумя типами линий — параллелями (параллель фиксирована определённой широтой) и меридианами (меридиан фиксирован определённой долготой).

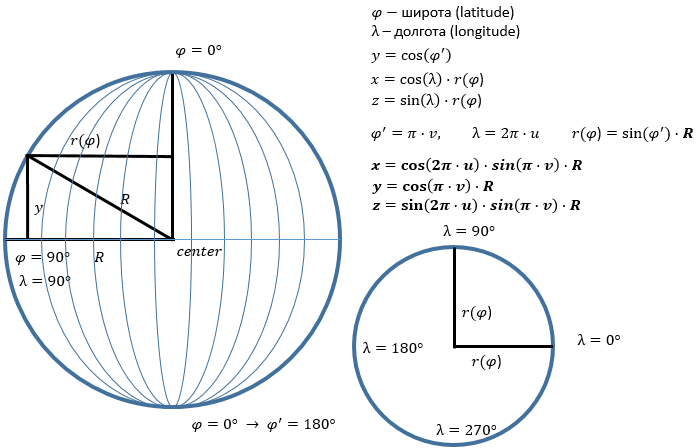
Этот подход хорошо сочетается с UV-параметризацией: мы будем делить сферу так же, как параллели и меридианы делят глобус, и обозначим широту как “φ”, а долготу как “λ”. Сделав несколько построений и применив тригонометрические правила, можно получить формулы, выводящие трёхмерный вектор (x, y, z) из двумерного вектора (u, v):

Полученный нами способ триагуляции аналогичен построению графика двумерной функции из прошлого примера. Только теперь вместо прямого вычисления (x, z) и вывода из них координаты “y” мы вводим сетку параметров (u, v) и выводим из них (x, y, z)

Видео:развертка конусаСкачать

Класс CIdentitySphere

Определение класса в целом похоже на CSolidFunctionSurface из предыдущей статьи, но в конструктор CIdentitySphere предаётся число делений по параллелям и по меридианам сферы, что позволяет задать детализацию сферы при её конструировании.

Вспомогательные функции CalculateTriangleStripIndicies (для распределения вершин по треугольникм) и DoWithBindedArrays (для привязк массивов данных к OpenGL) не изменились в сравнении с прошлым примером. Реализации конструктора и метода Draw просты:

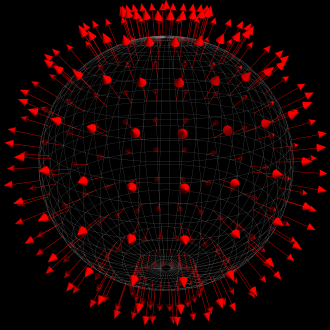
В методе Tesselate теперь вместо итерирования по (x,z) и вычисления y происходит итерирование по промежуточным параметрам (u,v) и вычисление ширины (latitude), долготы (longitude), а затем и позиции вершины (x,y,z) . Вычисление нормали выполняется легко, так как радиус, проведённый к точке сферы, уже перпендикулярен поверхности, а в единичной сфере радиус ещё и равен единице (т.е. не требует нормализации); это наблюдение проиллюстрировано на картинке:

Вспомогательная функция GetPositionOnSphere() по заданным (u,v) возвращает позицию вершины на единичной сфере, согласно ранее сделаному построению:

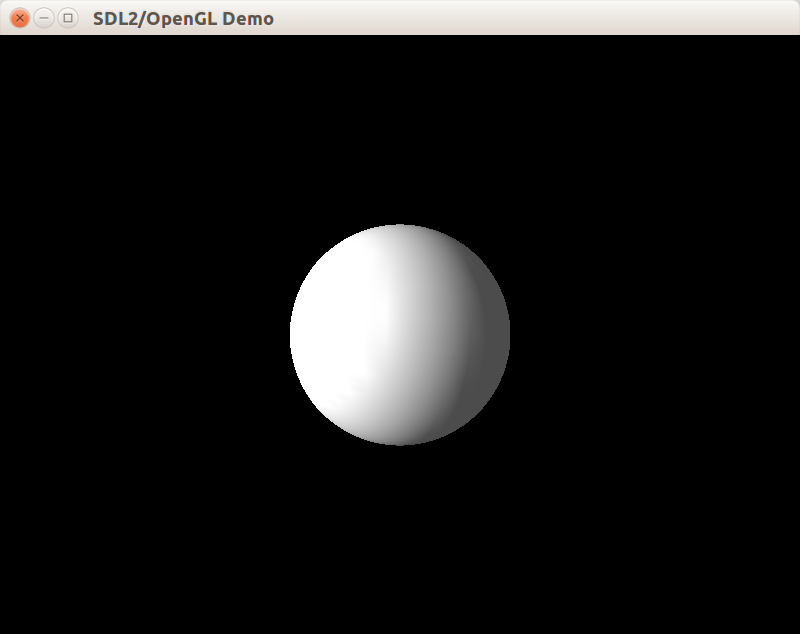
После добавления сферы в класс сцены с белым материалом мы получаем:

Видео:Создание сферы в компасеСкачать

Загрузка изображения как текстуры

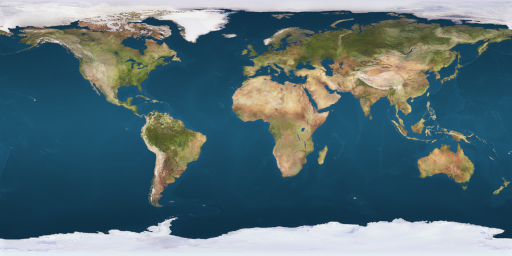
Настало время украсить поверхность сферы текстурой. Для примера мы возьмём текстуру Земли:

В OpenGL текстуры хранятся в видеопамяти, и загружаются программистом как массивы пикселей с помощью функции glTexImage2D. Чтобы получить массив пикселей из файла изображения средствами SDL2, нам потребуется загрузить объект SDL_Surface. Сделать это можно несколькими способами:

• с помощью функции SDL_LoadBMP можно загрузить изображения в формате BMP
• мы можем установить дополнительный модуль SDL_image и получить поддержку загрузки изображений в форматах PNG, JPEG, WEBP и TIFF с помощью функции IMG_Load

Формат BMP практически никак не сжимает данные о пикселях изображения: при размере 1000×1000 и формате пикселей RGBA размер файла будет порядка 4МБ (или чуть меньше в режиме RLE encoding). Чтобы избежать настолько ограниченного формата, установите SDL_image: для этого достаточно распаковать загруженный архив и совместить подкаталоги include, lib, bin с подкаталогами ранее установленной библиотеки SDL2.

Нам нужно обеспечить автоматическое управление памятью и обрабатывать ситуации, когда текстуру загрузить не удалось. Благодаря следованию правилам современного C++ и применению умных указателей, мы можем использовать механизм исключений и не бояться утечек ресурсов. Добавим обработку фатальных исключений программы в main:

main.cpp

Видео:Развертка цилиндраСкачать

Класс CFilesystemUtils

Этот класс будет предоставлять удобный интерфейс для загрузки ресурсов, построенный на основе Boost.Filesystem. Кроме того, класс займётся поиском ресурсов по относительным путям. Продемонстрируем определение этого класса:

Развернуть относительный путь в абсолютный можно двумя способами:

• если вы знаете точное местоположение корневого каталога, от которого отсчитываются относительные пути ресурсов, то можно использовать функцию boost::filesystem::absolute(relativePath, rootDir)
• если вы не знаете местоположение корневого каталога и воспользуетесь относительным путём, система сама развернёт путь с учётом текущего каталога (см. Working Directory на en.wikipedia.org) процесса программы.

Путь к текущему каталогу формируется простыми правилами, однако, новички в программировании всё равно часто путаются. Кроме того, выбор этого каталога может зависеть от действий пользователя. Куда надёжнее использовать путь к каталогу, в котором лежит исполняемый файл программы.

Мы воспользуемся универсальной функцией, которая определяет путь исполняемому файла на Windows, Linux и MacOSX, используя API операционной системы:

Полученный путь можно преобразовать в объект boost::filesystem::path , и затем получить родительский каталог для этого пути методом .parent_path() . Если мы добавим проверку существования сформированного пути, то мы можем написать универсальный статический метод класса CFilesystemUtils, который получает произвольный путь (возможно, относительный) и возвращает абсолютный путь.

Также нам пригодится статический метод, которая построчно загружает файл и помещает содержимое в экземпляр std::string :

Наконец, мы подготовим метод, который вызывает IMG_Load для загрузки изображения из файла в SDL_Surface. Чтобы обеспечить правильную работу с кириллическими и просто юникодными путями, нам потребуется преобразовать путь в однобайтовую строку в формате UTF-8 — именно в таком виде SDL принимает все пути к файлам.

Выше используется тип данных SDLSurfacePtr, который мы объявим как специализацию unique_ptr для SDL_Surface:

Видео:Пересечение конуса и сферы. Пошаговое видео. Инженерная графикаСкачать

Класс CTexture2D

Класс загузки и хранения для двумерной текстуры должен выполнять две задачи:

• предоставлять RAII интерфейс управления OpenGL-объектом “текстура”, для которого видеодрайвер выдаёт уникальный идентификатор типа unsigned
• выполнять как привязку текстуры к состоянию OpenGL, так и отмену ранее совершённой привязки

В OpenGL для привязки единственной текстуры к текущему контексту применяется функция glBindTexture. Заметим, что в более поздних версиях OpenGL были введены более удачные альтернативы, позволяющие использовать одновременно более одной текстуры; эти альтернативы имеют критическое значение для многих спецэффектов, но не интересуют нас в рамках данной статьи.

Последовательный вызов bind/unbind вполне приемлем для процедурного стиля программирования, но вызывает проблемы в программах, где возможен выброс исключений. Поэтому мы добавим к классу CTexture2D метод DoWhileBinded, принимающий функтор и выполняющий его в тот момент, когда текстура привязана к состоянию OpenGL.

Texture2D.h

В этом примере мы использовали макрос BOOST_SCOPE_EXIT_ALL, который доступен в библиотеках Boost, но только для компиляторов с поддержкой C++11. Макрос служит хорошей альтернативой написанию небольших RAII-классов.

Создание, удаление и привязка текстуры реализуются просто:

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Параметры наложения текстуры

Для того, чтобы нарисовать прямоугольник с наложенной на него текстурой, необходимо включить режим наложения двухмерной текстуры при помощи вызова функции glEnable с параметром GL_TEXTURE_2D, выбрать нужный текстурный объект при помощи glBindTexure, а затем

• либо привязать массив, содержащий текстурные координаты каждой вершины примитива, с помощью glTexCoordPointer
• либо задать текстурные координаты внутри glBegin/glEnd для каждо вершины отдельно с помощью семейства функций glTexCoord*
• либо иным способом передать этот атрибут для каждой вершины

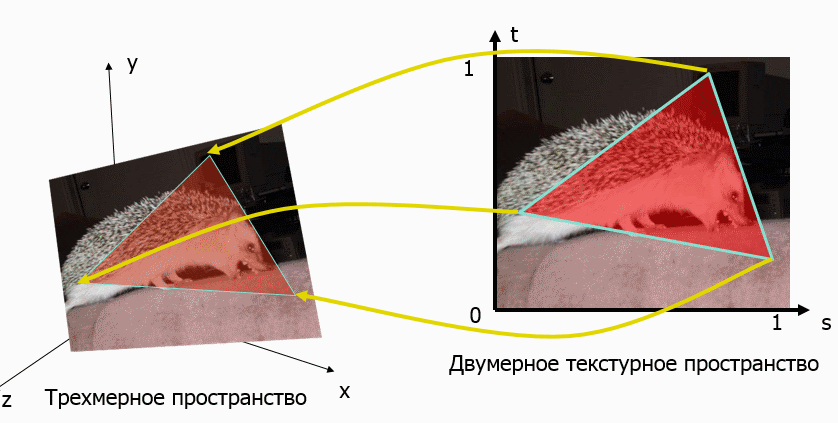
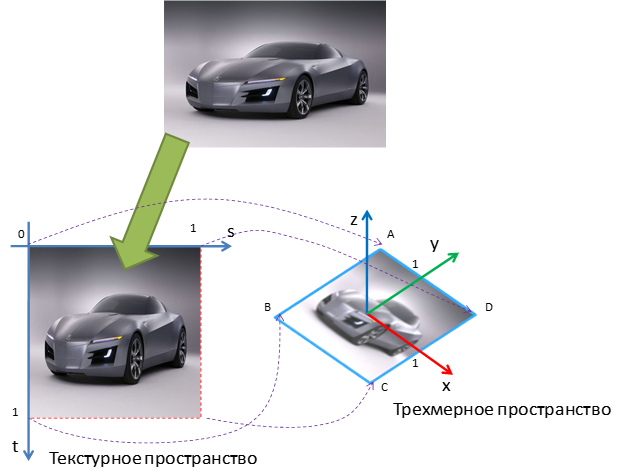
Текстурные координаты определяют способ наложения всей текстуры или её фрагмента на поверхность. Общий принцип проиллюстрирован ниже:

Текстурные координаты задаются в текстурном пространстве, задающем отображение текстурного изображения на диапазон координат от 0 до 1.

Есть ряд параметров, влияющих на наложение текстуры

оборачивание (wrapping), задающее поведение при выходе текстурных координат за границы [0;1]:

параметры адаптации текстуры при её масштабировании (filtering):

Подробнее о параметрах текстуры можно прочитать в статье на open.gl/textures. В рамках данного примера мы не используем дополнительные параметры.

Видео:Развертка треугольной равносторонней пирамиды. Урок24.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Класс для загрузки текстур

Класс CTexture2DLoader будет выполнять загрузку текстурного объекта из файла изображения, и кидать исключение в случае неудачной загрузки. Также будет возможность выбрать параметры, применяемые к текстуре, перед загрузкой.

Мы напишем вспомогательный статический метод CUtils::FlipSurfaceVertically , который обращается к пикселям SDL_Surface и зеркалирует их по вертикали. В результате текстура не окажется перевёрнутой из-за того, что OpenGL считает точкой отсчёта в текстуре левый нижний угол, а не левый верхний.

Теперь реализуем загрузку изображения сначала в оперативную память в виде матрицы пикселей, а затем и в видеопамять в виде текстуры OpenGL:

Наложение текстуры на объемные объекты

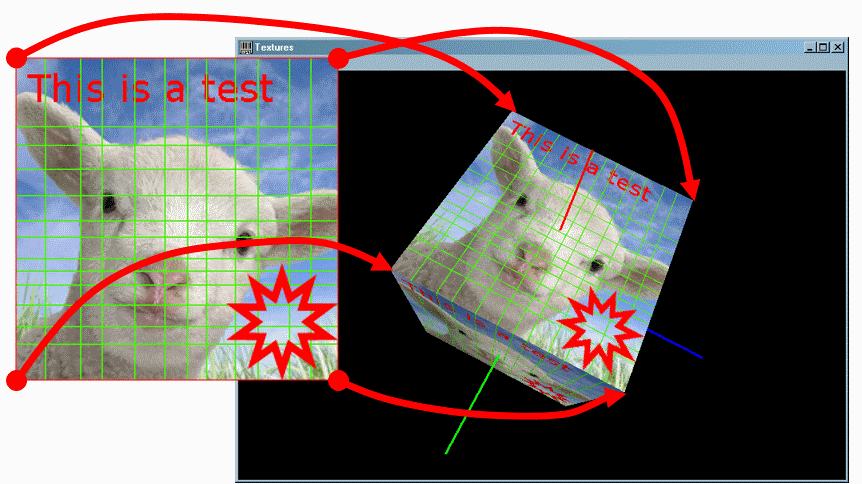
Визуализация объемного объекта в OpenGL сводится в визуализации плоских граней, аппроксимирующих поверхность данного объекта, поэтому принципиальных различий от наложения текстуры на плоские объекты нет. Основная наша задача – задать текстурные координаты вершин граней, чтобы получить желаемый результат.

Рассмотрим в данном примере расчет текстурных координат для сферы и куба, поскольку для таких фигур расчет текстурных координат выполняется достаточно просто. При наложении текстуры на более сложные объекты автоматический расчет текстурных координат, как правило, слишком сложен или не дает желаемых результатов. Поэтому дизайнеры трехмерных моделей выполняют наложение текстуры вручную при помощи специальных программ. Данная технология получила название UV mapping (U и V – распространенное имя для координатных осей в двухмерном текстурном пространстве):

UV mapping напрямую сочетается с UV-параметризацией. Благодаря этому, внедрить текстурные координаты в класс сферы для нас будет очень легко:

• SVertexP3N нужно расширить (и переименовать в SVertexP3NT2)
• в функции DoWithBindedArrays надо добавить привязку GL_TEXTURE_COORD_ARRAY

Структура SMeshP3NT3

Чтобы отделить логику триангуляции сферы от представлвения вершин, опишем в отдельной паре H-CPP структуру SMeshP3NT3. Таким будет заголовок:

В реализации нам потребуется привязать массивы атрибутов вершин, а затем нарисовать нужную группу примитивов (отдельные треугольники, полосу треугольников или веер треугольников):

Обновлённый класс CIdentitySphere

После модификаций определение этого класс будет выглядеть следующим образом:

В методе Tesselate надо передать (1-u,v) как две текстурные координаты. В этом трюке и заключается выгода UV-параметризации: нам не надо вычислять, как наложить текстуру на тело вращения.

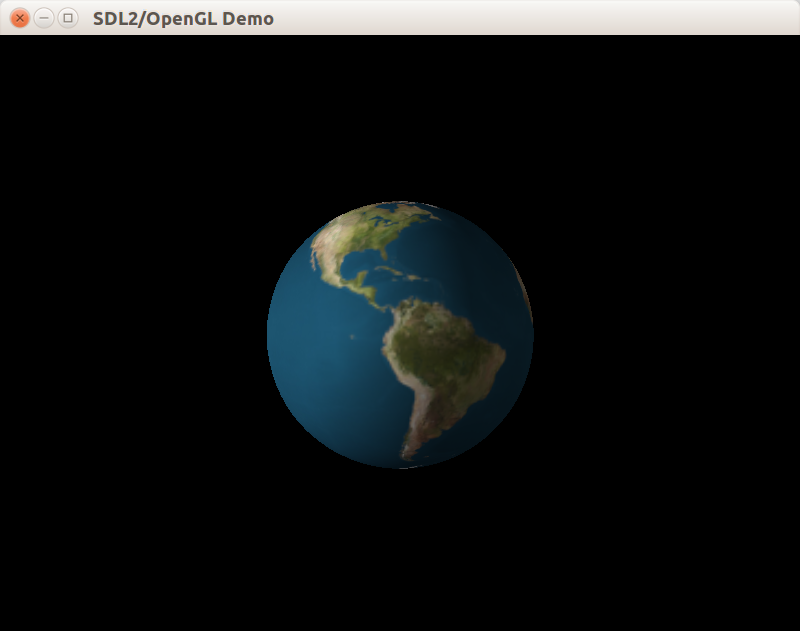
Загрузить текстуру для сферы в поле CWindow::m_pEarthTexture можно в методе OnWindowInit. В OnDrawWindow потребуется применить текстуру при рисованиию

После этого этапа получаем следующий результат:

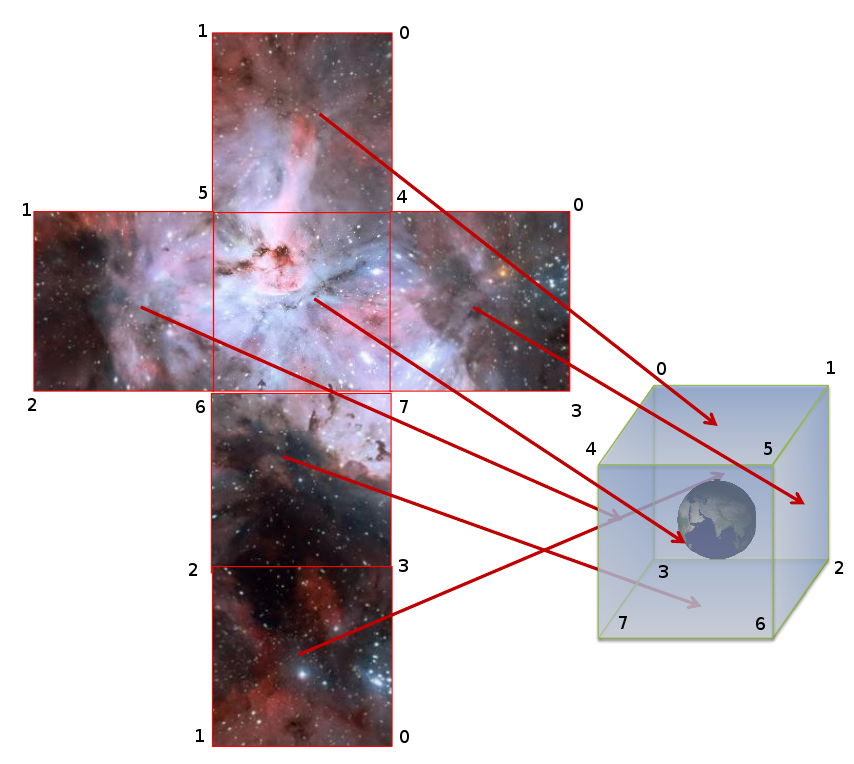
Готовым текстурный атлас для SkyBox

Для вывода коробки, рисующей окружающую среду вокруг камеры, нам потребуется несколько изображений.

Если хранить каждое изображение как отдельную текстуру, может возникнуть ряд проблем:

• может усложниться структура кода
• из-за постоянного переключения текстур на каждом кадре может снизиться производительность программы
• некоторые реализации OpenGL требуют, чтобы ширина и высота текстуры всегда были степенями двойки (2, 4, 8, …, 512, 1024 и т.д.); соблюдать эти требования вручную достаточно сложно

Для обхода этой проблемы мы реализуем идею текстурного атласа, позволяющего хранить целую серию мелких изображений. Эта идея также известна как Sprite Sheet, и она широко практикуется в мире Cocos2d-x:

Для упаковки текстур в такой атлас и вывода информации об упакованных изображениях в XML потребуется программа-упаковщик. В примерах был использован форк открытой программы Cheetah-Texture-Packer.

Полученный Texture Atlas есть в репозитории в файлах galaxy.plist и galaxy.png . Для загрузки атласа был написан класс CTexture2DAtlas, а также вспомогатлеьный класс CPropertyListParser, который с помощью библиотеки TinyXML загружает XML-описание спрайта и передаёт атласу информацию о фреймах. Изучить реализацию этих классов вы можете самостоятельно, а ниже приведено только определение класса:

Разработка куба для SkyBox

Мы обновим класс CIdentityCube, чтобы покрыть потребности Sky Box, которому нужны текстурные координаты на вершинах куба.

При выводе куба следует аккуратно накладывать текстуры, чтобы каждый из шести участков попал на свою грань куба, и чтобы ни одна текстура на грани не оказалась повёрнутой. В противном случае швы текстур между гранями не будут сочетаться, как на примере ниже:

Визуализируем наложение текстуры, сформированной в виде развёртки куба, на куб:

Пользуясь этой визуализацией, можно написать корректную реализацию единичного куба:

Класс CSkyBox

Данный класс не будет универсальным: он будет знать о конкретном текстурном атласе и использовать его для наложения текстуры на куб; также он будет использовать текущую матрицу моделирования-вида для рисования граней куба вокруг камеры на равном удалении независимо от поворота и положения камеры. Рассмотрим определение класса:

Реализация класса CSkyBox будет выглядеть следующим образом:

Код метода CSkyBox::Draw требует пояснений.

Во-первых, рисование куба мы будем выполнять, предварительно отключив модификацию буфера глубины при помощи функции glDepthMask(GL_FALSE) при отключенном тесте глубины. Благодаря этому содержимое буфера глубины после рисования sky box останется неизменным, при этом все фрагменты куба пройдут тест глубины. По этой же причине sky box должен быть нарисован первым, чтобы не стереть нарисованные до него объекты.

Во-вторых, центр куба привязан к точке наблюдателя. Это значит, что какой бы мы размер стороны куба ни выбрали, картинка не будет зависеть от длины стороны куба. Для того, чтобы привязать точку наблюдения к точке наблюдателя, необходимо заполнить нулями первые три элемента в четвертом столбце матрицы моделирования-вида.

В-третьих, здесь мы используем режим оборачивания текстурных координат GL_CLAMP_TO_EDGE. Его эффект проиллюстрирован ниже:

Результат

Вы можете взять полный пример к статье на github. А вот так выглядит окно после запуска: