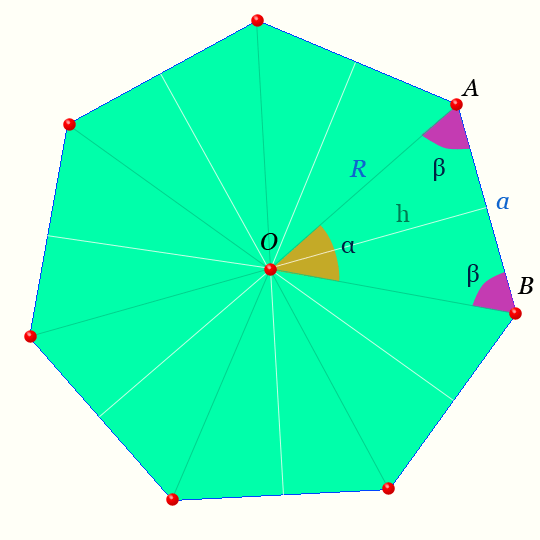
Правильный семиугольник — это такой семиугольник у которого все семь сторон равны и его семь углов равны.
Центр правильного семиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного семиугольника.
- Обозначения на рисунке для правильного семиугольника
- Основные формулы для правильного семиугольника
- Как начертить семиугольник
- Семиугольник, виды, свойства и формулы
- Семиугольник, виды, свойства и формулы.
- Семиугольник, выпуклый и невыпуклый семиугольник:
- Правильный семиугольник (понятие и определение):
- Свойства правильного семиугольника:
- Формулы правильного семиугольника:
- Семиугольник в природе, технике и культуре:
- Гептагон — Heptagon
- Обычный семиугольник
- Площадь
- Строительство
- Приближение
- Симметрия
- 🎥 Видео
Видео:Построение 7 угольника циркулем, приближенноеСкачать

Обозначения на рисунке для правильного семиугольника
| n=7 | число сторон и вершин правильного семиугольника, | шт |
|---|---|---|
| α | центральный угол правильного семиугольника, | радианы, ° |
| β | половина внутреннего угла правильного семиугольника, | радианы, ° |
| γ | внутренний угол правильного семиугольника, | радианы, ° |
| a | сторона правильного семиугольника, | м |
| R | радиусы правильного семиугольника, | м |
| p | полупериметр правильного семиугольника, | м |
| L | периметр правильного семиугольника, | м |
| h | апофемы правильного семиугольника, | м |
Видео:1 2 3 деление окружности на 7 равных частейСкачать

Основные формулы для правильного семиугольника
Периметр правильного семиугольника
Полупериметр правильного семиугольника
Центральный угол правильного семиугольника в радианах
Центральный угол правильного семиугольника в градусах
Половина внутреннего угла правильного семиугольника в радианах
Половина внутреннего угла правильного семиугольника в градусах
Внутренний угол правильного семиугольника в радианах
Внутренний угол правильного семиугольника в градусах
Видео:Геометрия - Построение семиугольника и звездыСкачать

Как начертить семиугольник
При необходимости построить правильный семиугольник обычно возникают небольшие сложности. Однако если вам не нужна идеальная точность чертежа и погрешность в 0,2% не является для вас критичной, вы можете легко произвести построение такого многоугольника при помощи циркуля и обычной линейки.
Чтобы начать построение, начертите произвольную окружность и обозначьте ее центр буквой О. Затем проведите радиус этой окружности в любом направлении. Точку пересечения радиуса с окружностью обозначьте буквой А. После этого переставьте циркуль в точку А и проведите окружность или дугу того же радиуса, что и у исходной окружности (ОА). Данная дуга пересечет исходную окружность в двух точках. Обозначьте их буквами В и С.
Соедините две полученные точки. При этом отрезок ВС пересечет радиус ОА. Точку их пересечения обозначьте буквой D. Образовавшиеся при этом отрезки ВD и DC будут равны между собой и каждый из них будет приблизительно равен стороне правильного семиугольника, который можно вписать в исходную окружность.
Отмерьте циркулем расстояние ВD (или DC) и, начиная с любой точки на окружности, отложите это расстояние шесть раз. Затем соедините все семь точек. Так вы получите семиугольник, который с небольшой погрешностью можно назвать правильным. Все его стороны и углы будут приблизительно равны.
Есть и другой способ построения правильного семиугольника. Для начала начертите произвольную окружность и проведите два взаимно перпендикулярных диаметра этой окружности. Назовите их АВ и СD. Далее один из диаметров (например, АВ) разделите на семь равных частей. Например, если длина вашего диаметра составляет 14 см, то длина каждой его части будет равна 2 см. В результате на данном диаметре должно появиться шесть отметок.
Затем переставьте циркуль в один из концов данного диаметра (например, В) и проведите из этой точки дугу, радиус которой будет равен диаметру исходной окружности (АВ). После этого продлите второй диаметр (СD) до пересечения с построенной дугой. Полученную точку обозначьте буквой Е.
Теперь из точки Е проведите прямые, проходящие только через четные или только через нечетные деления на диаметре АВ. Например, через второе, четвертое и шестое деления. Точки пересечения этих прямых с окружностью будут тремя из семи вершин вашего будущего многоугольника. Обозначьте их F, G и H. Четвертой вершиной будет точка А (в том случае, если вы проводили прямые через четные отметки) или точка В (если одна из прямых прошла через ближайшую к точке А отсечку).
Чтобы найти пятую, шестую и седьмую вершины, проведите из точек F, G и H прямые, строго перпендикулярные диаметру АВ. Те точки, в которых эти прямые пересекут противоположную сторону окружности, будут тремя искомыми вершинами. Для завершения построения вам нужно будет соединить все семь вершин.
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Видео:Как разделить окружность на семь равных частей. How to divide a circle into seven equal partsСкачать

Семиугольник, виды, свойства и формулы
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Семиугольник, виды, свойства и формулы.
Семиугольник — это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник, выпуклый и невыпуклый семиугольник
Правильный семиугольник (понятие и определение)
Свойства правильного семиугольника
Формулы правильного семиугольника
Семиугольник в природе, технике и культуре
Шестиугольник, семиугольник, восьмиугольник
Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ СЕМИУГОЛЬНИК [construction of regular heptagon]Скачать
![ПОСТРОИТЬ ПРАВИЛЬНЫЙ СЕМИУГОЛЬНИК [construction of regular heptagon]](https://i.ytimg.com/vi/br29b-dYXJE/0.jpg)
Семиугольник, выпуклый и невыпуклый семиугольник:
Семиугольник — это многоугольник с семью углами.
Семиугольник — это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый семиугольник — это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Звёздчатый семиугольник — семиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого семиугольника могут пересекаться между собой.
Рис. 1. Выпуклый семиугольник
Рис. 2. Невыпуклый семиугольник
Сумма внутренних углов любого выпуклого семиугольника равна 900°.
Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Правильный семиугольник (понятие и определение):
Правильный семиугольник — это правильный многоугольник с семью сторонами.
В свою очередь правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Правильный семиугольник — это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈ 128,571°.
Рис. 3. Правильный семиугольник
Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный семиугольник можно невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Видео:Геометрия - Построение восьмиугольникаСкачать

Свойства правильного семиугольника:
1. Все стороны правильного семиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a7.
2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = 128 4/7° ≈ 128,571°.
Рис. 4. Правильный семиугольник
3. Сумма внутренних углов любого правильного семиугольника равна 900°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.
Рис. 5. Правильный семиугольник
5. Количество диагоналей правильного семиугольника равно 14.
Рис. 6. Правильный семиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный семиугольник
Видео:Деление окружности на 7 частейСкачать
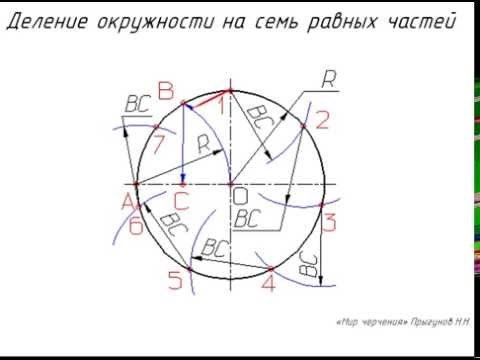
Формулы правильного семиугольника:
Пусть a — сторона семиугольника, r — радиус окружности, вписанной в семиугольник, R — радиус описанной окружности семиугольника, P — периметр семиугольника, S — площадь семиугольника.
Формулы стороны правильного семиугольника:
Формулы периметра правильного семиугольника:
Формулы площади правильного семиугольника:
Формулы радиуса окружности, вписанной в правильный семиугольник:
Видео:Как определить расположение чисел на единичной окружностиСкачать

Семиугольник в природе, технике и культуре:
В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.
Некоторые виды кактусовых имеют форму звездчатого семиугольника.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности 974
Видео:Геометрия - Построение шестиугольникаСкачать

Гептагон — Heptagon
В геометрии , A — угольник представляет собой семь-сторонний многоугольник или 7-угольник.
Угольник иногда называют septagon , используя «sept-» (в Пропуска из septua- , А латинский -derived числового префикса , а не гептабромированные , А греческий -derived числового префикс, оба родственны) вместе с греческим суффиксом «-агон» означает угол.
Видео:Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Обычный семиугольник
Регулярно угольник , в котором все стороны и все углы равны, имеет внутренние углы из его / 7 радиана (128 4 / 7 градусов ). Его символ Шлефли — .
Площадь
Площадь ( A ) правильного семиугольника с длиной стороны a определяется по формуле:
Это можно увидеть, разделив семиугольник с единичной стороной на семь треугольных «кусочков пирога» с вершинами в центре и в вершинах семиугольника, а затем разделив пополам каждый треугольник, используя апофему в качестве общей стороны. Апофема составляет половину котангенса, а площадь каждого из 14 маленьких треугольников составляет одну четвертую апофемы.
Точное алгебраическое выражение дается в комплексных числах следующим образом:
в котором мнимые части компенсируют друг друга, оставляя выражение с действительным знаком. Это выражение не может быть алгебраически переписано без комплексных компонентов, поскольку кубическая функция, которая служит минимальным многочленом, есть casus unducibilis .
Площадь правильного семиугольника, вписанного в круг радиуса R, равна площади самого круга, таким образом, правильный семиугольник заполняет приблизительно 0,8710 его описанной окружности .
Строительство
Поскольку 7 — простое число Пьерпона, но не простое число Ферма , правильный семиугольник нельзя построить с помощью циркуля и линейки, но можно построить с помощью отмеченной линейки и циркуля. Это самый маленький правильный многоугольник с этим свойством. Такой тип конструкции называется конструкцией neusis . Его также можно построить с помощью циркуля, линейки и трисектора. Невозможность построения линейки и циркуля следует из наблюдения, которое является нулем неприводимой кубики x 3 + x 2 — 2 x — 1 . Следовательно, этот многочлен является минимальным многочленом от 2cos ( 2π ⁄ 7 ), тогда как степень минимального многочлена для конструктивного числа должна быть степенью 2.
Жерар Т Хофт показывает правильный семиугольник, состоящий всего из 15 полосок Meccano с размером стержней 8 и 11.
Конструкция состоит из двух равнобедренных треугольников, на которых закреплены остальные стержни. Сторона правильного семиугольника a , сторона более короткого равнобедренного треугольника e и сторона более длинного равнобедренного треугольника d удовлетворяют условиям
Формула получена из формулы Гептагонального треугольника :
Небольшие возможные конструкции семиугольника:
| Семиугольник | а | d | е |
|---|---|---|---|
| 1 | 3 | 4 | 1 |
| 2 | 8 | 11 | 6 |
| 3 | 33 | 46 | 29 |
| 4 | 40 | 53 | 6 |
| 5 | 55 | 74 | 27 |
Наименьший семиугольник меккано 1:
Приближение
Примерное значение для практического использования с погрешностью около 0,2% показано на чертеже. Его приписывают Альбрехту Дюреру . Пусть A лежит на окружности описанной окружности. Нарисуйте дугу BOC . Затем дает приближение для края семиугольника.
Это приближение используется для стороны семиугольника, вписанного в единичный круг, в то время как точное значение .
Пример для иллюстрации ошибки:
при радиусе описанной окружности r = 1 м абсолютная погрешность 1-й стороны будет приблизительно -1,7 мм.
Meccano аппроксимирует семиугольник. Размеры штанги — 20, 36 и 45.
Построение аппроксимации меккано может быть выполнено с помощью одиннадцати столбцов размером 20, 36 и 45. Эти значения оставляют ошибку около 0,1%.
Симметрия
Симметрии правильного семиугольника. Вершины раскрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. В центре даны приказы гирации.
Регулярно угольник относится к D 7h точечной группы ( Шенфлиса обозначение ), порядка 28. Элементы симметрии: 7-кратное правильное вращение оси С 7 , 7-кратное неправильное вращение оси а, S 7 , 7 вертикальные плоскости зеркала, σ v , 7 2-кратные оси вращения C 2 в плоскости семиугольника и горизонтальная зеркальная плоскость σ h также в плоскости семиугольника.
🎥 Видео
Построение пятиугольника циркулемСкачать

Красивое деление окружности на 20 частей циркулемСкачать

Построение 8 угольника циркулемСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на 12 равных частейСкачать

Построение 12 угольника циркулемСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать