Решение задач окружности паскалю (8 видео)

Опредилить принадлежность точки кругу

Содержание

Задача
Решение
Задачи по Pascal. Вычислить длину окружности, площадь круга и объем шара одного и того же заданного радиуса.
Решение задачи
«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС» методическая разработка по информатике и икт (9 класс) на тему
Скачать:
Предварительный просмотр:
Введение
Основная часть
Задания, которые рассматриваются на занятии:
Проверяемые элементы содержания
Основное содержание теоретической части
Задания на этапе первичного закрепления
🎬 Видео

Задача

Даны координаты точки и радиус круга с центром в начале координат. Определить, принадлежит ли данная точка кругу.

Решение

x, y, r — координаты точки и радиус круга;
r_xy — длина гипотенузы (расстояния от начала координат до точки).

Алгоритм решения задачи:

Следует рассмотреть прямоугольный треугольник, один катет которого лежит на любой оси, а другой является перпендикуляром к этой оси из заданной точки. В этом случае длины катетов равны значениям x и y, а гипотенуза является отрезком, соединяющим начало координат с точкой. Если этот отрезок не больше радиуса круга, то делается вывод, что точка принадлежит кругу.

Длина гипотенузы находится по теореме Пифагора.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Задачи по Pascal. Вычислить длину окружности, площадь круга и объем шара одного и того же заданного радиуса.

Условие задачи: Вычислить длину окружности, площадь круга и объем шара одного и того же заданного радиуса (Язык Pascal)

Сложность: легкая.

Видео:Вычисление площади круга и длинны окружности по заданному радиусу в Паскаль с применением константыСкачать

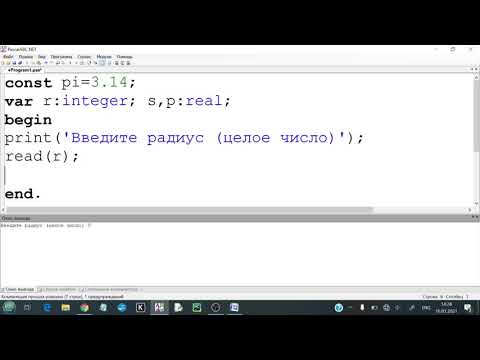
Решение задачи

Для начала продумаем наше решение. Сначала введем радиус, потом просто подставим в формулы:

Сначала формулы. Первая у нас это длина окружности :

Дальше площадь круга :

Ну и объема шара :

Для того чтобы решить задачу нам понадобятся следующие переменные :

Переменная R — для радиуса
Переменная dlOkr — для длины окружности
Переменная sqKrug — для площади круга
Переменная Vshara — для объема шара

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»
методическая разработка по информатике и икт (9 класс) на тему

Занятие, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Практическая работа на тему

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»

В данной разработке представлены задачи с геометрическим содержанием по теме «Окружность и круг» для 9 класса. Для этих задач разработаны алгоритмы и программы на псевдокоде и языке Паскаль. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе.

Видео:Пример решения задач на Pascal #1Скачать

Скачать:

Вложение	Размер
prakticheskoe_zanyatie_algoritmy_geom_zadachi_shirobokovagi.docx	566.42 КБ

Видео:Окружность. 7 класс.Скачать

Предварительный просмотр:

учитель математики информатики

Видео:Паскаль с Нуля. Переменные, Оператор присваивания, Оператор ввода. Урок 2Скачать

Введение

Одна из главная задач ФГОС, которые призваны реализовать развивающий потенциал общего среднего образования — готовить своих учеников к жизни, обеспечить ребенку общекультурное, личностное и познавательное развитие, вооружить умением учиться. Перед выпускниками, вступающими в самостоятельную жизнь, встаёт проблема решать новые, неизвестные задачи, которые неизбежно встанут перед ними. Результат образования можно «измерить» умением успешно решать такие задачи.

В новых стандартах метапредметным результатам уделено особое внимание, поскольку именно они обеспечивают более качественную подготовку учащихся к самостоятельному решению проблем, с которыми встречается каждый человек на разных этапах своего жизненного пути в условиях быстро меняющегося общества. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе. Программирование обучает методам мышления, общим подходам к постановке и решению задач. Поэтому выбрана тема занятия, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Основная часть

Тема занятия : Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг».

Видео:Паскаль с Нуля. Арифметические действия, DIV, MOD. Урок 3Скачать

Задания, которые рассматриваются на занятии:

вычисление длины окружности по заданному радиусу;
нахождение площади круга, ограниченного окружностью заданного радиуса;
нахождение площади кольца по внутреннему и внешнему радиусам;
вычисление расстояния между двумя точками с заданными координатами;
найти площади сектора по радиусу и дуге;
определение минимального радиуса круга, в который попадают точки, заданные координатами на плоскости;

Для решения задач используем линейные структуры, ветвления и циклы.

Видео:Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

Проверяемые элементы содержания

Формальное исполнение алгоритма, записанного на естественном языке или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд.

Знание основных конструкций языка программирования, понятия переменной, оператора присваивания.

Умение исполнить алгоритм для конкретного исполнителя с фиксированным набором команд.

Анализ алгоритма, содержащего вспомогательные алгоритмы, цикл и ветвление.

Умение анализировать результат исполнения алгоритма.

Видео:Линейные программы. Решение задач. Ч.1.Скачать

Основное содержание теоретической части

Алгоритмы работы с величинами: константы, переменные, понятие типов данных, ввод и вывод данных.

Структура программы на языке Паскаль. Представление данных в программе. Правила записи основных операторов: присваивания, ввода, вывода, ветвления, циклов.

Этапы решения задачи с использованием программирования: постановка задачи, формализация, алгоритмизация, кодирование, отладка, тестирование.

Практика на компьютере: знакомство с системой программирования на языке Паскаль; ввод, трансляция и исполнение данной программы; разработка и исполнение линейных, ветвящихся и циклических программ.

Переменная, константа, операторы ввода/вывода, оператор присваивания, арифметические операции с переменными.

Создание с использованием свойств геометрических фигур математических моделей для решения задач практического характера и задач из смежных дисциплин (для данного занятия – конкретно геометрии), исследовать полученные модели и интерпретировать результат.

Задачи на применение линейных алгоритмических структур. В ходе решения задач повторяются формулы курса геометрии 9 класса: вычисление длины окружности, площади круга, площади кольца, площади сектора, расстояния между двумя точками на плоскости, заданных координатами (метод координат в курсе геометрии).

Видео:Решение задач на Pascal #7 | Цикл FORСкачать

Задания на этапе первичного закрепления

Рассмотрим подробно задачи геометрического содержания с постановкой, математической моделью, алгоритмом, программой на языке Паскаль и полученными результатами (скриншот).

Задача 1. Вычислить длину окружности по заданному радиусу.

Результат – найти длину окружности.
Исходные данные – радиус окружности.
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительное число.

Математическая модель. Вычислить длину окружности по формуле

Описать переменные. Ввести данные.

Вычислить по формуле длины окружности C= 2*π*R.

Write( ‘Введите радиус окружности R= ‘ );

WriteLn( ‘Длина окружности С= ‘ ,C: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 37, 57344814. Верно.

Задача 2. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

Результат – площадь круга.
Исходные данные – длина окружности.
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительное число.

Математическая модель. Выразить радиус R из формулы длины окружности C= 2*π*R. Вычислить радиус R=C/(2* π). Вычислить площадь круга по формуле S= .

Описать переменные. Ввести данные.

Выразить радиус R из формулы длины окружности.

Вычислить радиус по формуле R=C/(2* π). Вычислить площадь круга по формуле S= .

Write( ‘Введите длину окружности С= ‘ );

WriteLn( ‘Площадь круга = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверка результата с помощью калькулятора, получим число 426, 5116724. Значит, программа правильна.

Задача 3. Найти площадь кольца, внутренний радиус которого равен r, а внешний – заданному числу R (R> r).

Результат – найти площадь кольца.
Исходные данные – внутренний радиус равен r, а внешний – R (R> r).
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительные числа.

Математическая модель. Найдём площадь кольца по формуле S к =π*(R*R-r*r), где – R — внешний радиус, r-внутренний радиуc, (R> r).

Описать переменные. Ввести данные.

Вычислить по формуле площадь кольца по формуле S к =π*(R*R-r*r).

Writeln( ‘Введите радиусы окружностей R2 и R1 ‘ );

S := pi * (R2 * R2 — R1 * R1);

WriteLn( ‘Площадь кольца S = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 12, 56637061. Верно.

Задача 4. Вычислить расстояние между двумя точками с координатами X1, Y1 и X2, Y2.

Результат – найти расстояние R между двумя точками на плоскости.
Исходные данные – даны координаты точек (X1, Y1) и (X2, Y2).
Ограничения на результат – ограничение на расстояние R>=0
Ограничения на исходные данные — ограничений на координаты нет.

Математическая модель. Выведем формулу для вычисления расстояния между двумя точками на плоскости.

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x b — x a ;
BC = y b — y a .

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости: AB = .

Описать переменные. Ввести данные.

Вычислить расстояние между точками по формуле R= .

Напишем алгоритм на псевдокоде

* вывод (‘Введите координаты (x и y) точки 1’)

* вывод (‘Введите координаты (x и y) точки 2’)

* R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

* вывод (‘расстояние между точками 1 и 2 равно ‘, R:10:3);

X1, X2, Y1, Y2, R: Real ;

Writeln( ‘Введите координаты (x и y) точки 1’ );

Writeln( ‘Введите координаты (x и y) точки 2’ );

R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

Write( ‘расстояние между точками 1 и 2 равно ‘ , R: 10 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 4. Верно.

Задача 5. Найти площадь сектора, радиус которого равен 15.4, а дуга содержит заданное число радиан ϕ .

Результат – площадь сектора.
Исходные данные – величина угла в радианах.
Ограничения на результат – положительное число.
Ограничения на исходные данные – значение дуги в радианах меньше, чем 2π ≈ 6.28. Иначе сектор будет по величине больше круга.

Модель. Выведем формулу для вычисления площади сектора через угол, выраженный в радианах. Сектор круга ограничивается дугой между двумя точками А и В на окружности и двумя радиусами, проведёнными из концов дуги (точек А и В) к центру круга.

Два радиуса делят всю площадь круга на 2 сектора. Если угол между этими радиусами будет развёрнутым (180 0 ), то эти секторы будут между собой равны. Площадь сектора круга – это часть площади всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число S= . Площадь кругового сектора в радиан (полукруга) равна . Поэтому площадь сектора в один радиан в π раз меньше, т.е. равна : π. Значит, площадь сектора в α радиан равна =

* вывод (‘Введите величину дуги кругового сектора (в радианах)’)

* вывод (‘Площадь кругового сектора =’, S:8:2)

write(‘Введите величину дуги кругового сектора (в радианах) ‘);

writeln(‘Площадь кругового сектора = ‘, S:8:2)

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора.

Задача 6. Даны координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn,yn). Определить минимальный радиус круга, в который попадают все эти точки. Центр круга находится в начале координат.

Результат – определить минимальный радиус круга, в который попадают точки с заданными координатами.
Исходные данные – координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn, yn).
Ограничения на результат – неотрицательное действительное число.
Ограничения на исходные данные – координаты точек выражаются действительными числами, количество точек N — натуральное число.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОД: Радиус круга с центром в начале координат вычисляется по формуле R= . Для наглядности рисунок.

АЛГОРИТМ. Вычисляем радиус (расстояние от начала координат до точки) для каждой точки, выбираем минимальное значение. Сравниваем два числа, наименьшее значение записываем как минимум. Это и будет минимальным значением радиуса. Так как количество точек известно, организуем цикл с параметром.