Равносторонние треугольники 7 класс

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Равнобедренный треугольник. 7 класс.Скачать

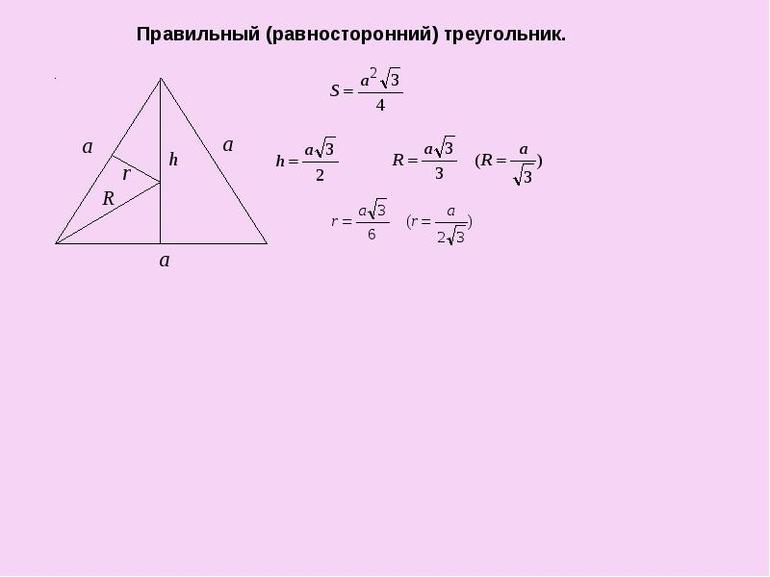
Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:Геометрия Равносторонний треугольникСкачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

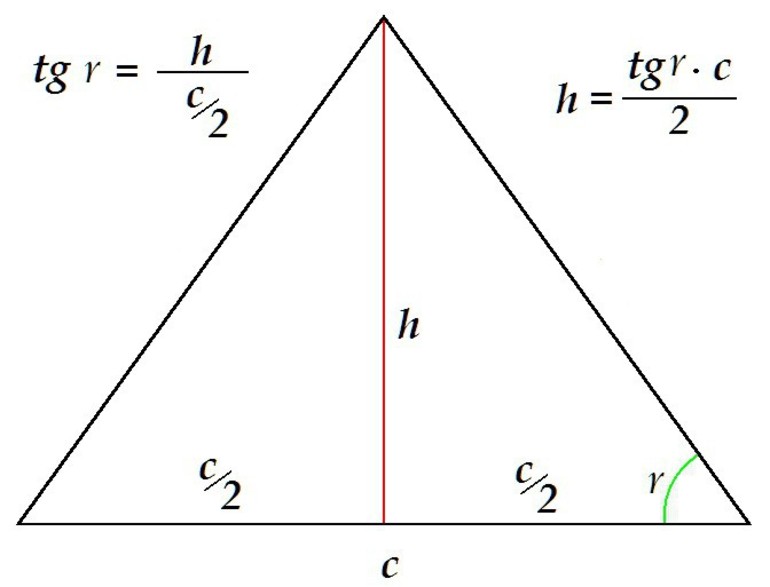
1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Конспект урока геометрии «Равнобедренный и равносторонний треугольники» (7 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Урок 7 класс.docx

Тема урока: Равнобедренный, равносторонний и разносторонний треугольник.

Цель урока: ввести определение равнобедренного, равностороннего и разностороннего треугольников и его элементов; научить решать задачи на вычисление периметра;

развивать умение анализировать, сравнивать, делать выводы;

воспитывать познавательный интерес к предмету.

Тип урока: урок изучения нового материала с использованием системно-деятельностного подхода.

Оборудование: компьютер, мультимедийный проектор, компьютерная презентация.

1. Организация начала урока.

Сегодня у нас урок геометрии, На протяжении всего урока вы будите создавать своего спутника по стране Геометрия.

2. Актуализация опорных знаний.

(Треугольник)

● Как вы думаете почему зашифровано именно это слово?

А какая фигура называется треугольником?

Из трёх точек состоит из века в век,

Потому что так придумал человек.

Не лежат при этом точки на прямой,

Хоть и хочется друг к другу им домой.

Три отрезка их всю жизнь соединяют.

И вершинами те точки называют,

А отрезки сторонами величают.

● Какие треугольники называются равными?

● Как читается 1 признак равенства треугольников.

Какое условие необходимо добавить, чтобы доказать равенство треугольников по

Как читается 2 признак равенства треугольников. Какое условие необходимо добавить, чтобы доказать равенство треугольников п о второму признаку .

Ответ: ∠ L К P = ∠ K Р D .

Пользуясь данными рисунка, отметьте правильный ответ: (обведите кружком букву)

А) 4 см; Б) 6 см; В) 8 см

А) 120 о ; Б) 60 о ; В) 100 о

3)

А) 60 о ; Б) 120 о ; В) 50 о

Проверяем правильный ответ. Первый вариант АБА

По полученным результатам постройте первые элементы вашего спутника

Форма лица: а) круг; б) квадрат; в) треугольник

Форма тела: а) квадрат; б) прямоугольник; в) треугольник

Форма рук: а) отрезок; б) прямоугольник; в) овал

— Устали? Сцепите руки в замок над головой и потянитесь. Учёные говорят, что в этот момент выделяется гормон удовольствия.

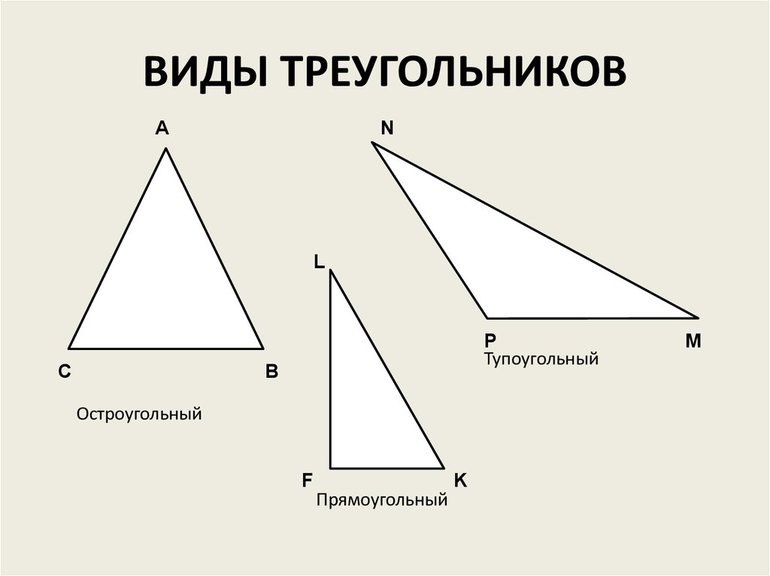
● Какими могут быть треугольники в зависимости от величины углов? Дайте определение

Узнает очень просто меня любой дошкольник.

Я тупо-, прямо-, остро-угольный треугольник.

Как вы думаете, существуют ли виды треугольника по другим элементам? Каким?

Какова тема сегодняшнего урока?

Что вы хотите узнать по этой теме?

Цель : узнать о видах треугольника по сторонам, научиться их определять, научиться решать задачи.

3. Изучение нового материала.

● Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства

которой человек узнал ещё в глубокой древности. Например, то, что в равнобедренном

треугольнике, с которым мы сегодня познакомимся, углы при основании равны, было известно

ещё древним вавилонянам 4000 лет назад. Равнобедренный треугольник обладает ещё рядом

геометрических свойств, которые всегда имели широкое применение в практической жизни.

Для того, чтобы научиться определять вид треугольника, необходимо выяснить, почему он так называется.

Формируем 3 «Лаборатории». Выберите старшего в группе.

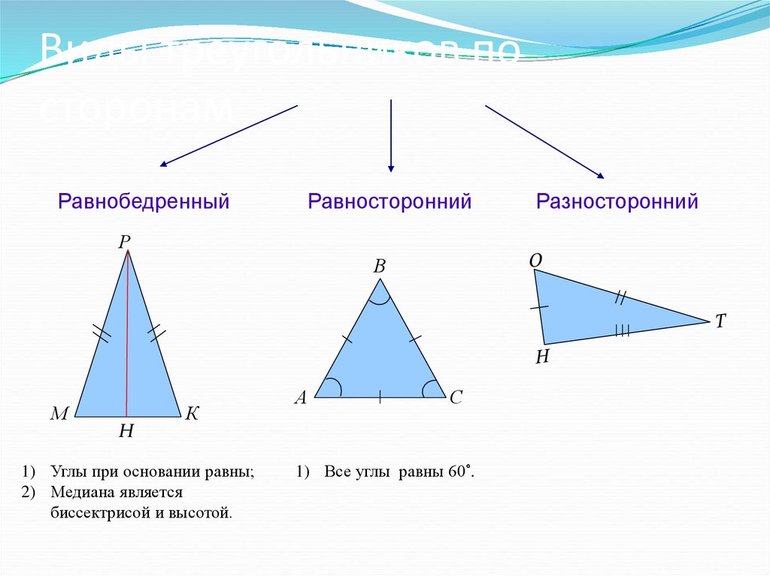
1) Выяснить какие треугольники называются равнобедренными, равносторонними и разносторонними.

2) Дать определение каждому из них.

3) Познакомиться с названием сторон равнобедренного треугольника.

(ребятам раздаются листы с печатной основой лабораторной работы в файлах)

Оборудование: масштабная линейка.

ЛАБОРАТОРНАЯ РАБОТА В файле у вас 5 треугольников, разделите их между собой и выполните задание, написанное ниже, потом вместе под руководством старшего запишите выводы.

Задание 1 . Измерьте стороны треугольника, запишите результат измерений:

АВ = ………см; BC = ………см; AC = ………см;

MN = ………см; NK = ………см; MK = ………см;

ST = ……… см ; TR = ……… см ; SR = ……… см ;

DE = ……… см ; EF = ……… см ; DF = ……… см ;

OQ = ……… см ; QG = ……… см ; OG = ……… см .

Задание 2 . Треугольники ∆ ABC , ∆ MNK , ∆ STR — равнобедренные. Сравните результаты измерений и дайте определение равнобедренного треугольника:

Треугольник ∆ OQG – равносторонний. Посмотрите на результаты измерений, дайте определение равностороннего треугольника:

ОПРЕДЕЛЕНИЕ. Треугольник называется равносторонним , если………………

Можно ли равносторонний треугольник назвать равнобедренным.

А равнобедренный – равносторонним.

Используя определения равностороннего и равнобедренного треугольника, дайте определение разностороннего треугольника:

ОПРЕДЕЛЕНИЕ. Треугольник называется разносторонним , если………………

Найдите разносторонний треугольник на рисунке ∆____________

Задание 3. С помощью рисунка 153 на стр. 61 учебника, выясните, как называются стороны равнобедренного треугольника, подпишите их

В каждом равнобедренном треугольнике найдите боковые стороны и основание:

∆ АВС – боковые стороны:………………..; основание…………..;

∆ MNK – боковые стороны:………………..; основание…………..;

∆ STR – боковые стороны:………………..; основание…………..;

Можно ли равносторонний треугольник назвать равнобедренным.

А равнобедренный – равносторонним.

Лаборатория закрывается. Все рассаживаются по своим местам.

Физкультминутка . Нарисуйте глазами:

Прямоугольный равнобедренный треугольник

Остроугольный равнобедренный треугольник

Тупоугольный равнобедренный треугольник

4. Первичное закрепление нового материала.

1 .В равнобедренном треугольнике АМК АМ = АК. Назовите основание и углы при основании

этого треугольника. (МК, М, К)

Нарисуйте глаза вашему спутнику в форме, если:

А) треугольник; Б) овал; В) круг

2. Дан равнобедренный треугольник СОР c основанием СР. Назовите боковые стороны и углы при

основании этого треугольника. (СО и ОР, С, Р)

3 . Определите вид треугольников, изображённых на рисунке, почему?

У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании,

угол, противолежащий основанию (угол при вершине равнобедренного треугольника) .

● Обратите внимание на треугольник SPT. В этом треугольнике основанием может быть любая сторона, а боковыми – любые две его стороны, так как у него все стороны равны.

Нарисуйте своему спутнику столько кудряшек, сколько равнобедренных треугольников на слайде.

1 .В равнобедренном треугольнике боковая сторона равна 9см, а основание 5см. Вычислите

периметр треугольника. Ответ: 23см.

2. В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите

боковую сторону треугольника. Ответ:5см.

3 . В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите

основание треугольника. Ответ:10см.

4 . В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.

6. Подведение итогов.

Молодцы! Настало время подвести итоги.

Какие цели мы поставили на урок?

Как вы думаете, достигли мы их?

Нарисуйте своему спутнику нос в такой форме, который соответствует картинке с равнобедренным треугольником.

Форма носа: а) картошкой б) с горбинкой в) треугольник г) круглый

Сравните получившегося у вас спутника по стране Геометрия с образцом (учитель вывешивает на доске).

Поверьте количество верных элементов

Все элементы верны «5»

Я предлагаю нарисовать ему губы в зависимости от вашего настроения на уроке.

7. Домашнее задание.

§ 9 выучить определения

Выбранный для просмотра документ Урок Геометрии 7.pptx

Описание презентации по отдельным слайдам:

Форма лица: А) круг; Б) квадрат; В) треугольник Форма тела: А) квадрат; Б) прямоугольник; В) треугольник Форма рук: А) отрезок; Б) прямоугольник; В) овал

Виды треугольников по углам

Равнобедренный, равносторонний и разносторонний треугольники

∆АМК – равнобедренный АМ = МК А М К

∆СОР – равнобедренный СР – основание С О Р

боковые стороны; основание; углы при основании; угол, противолежащий основанию

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 989 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия 7 класс (Урок№32 - Повторение. Равнобедренный треугольник и его свойства.)Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 527 376 материалов в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 9. Равнобедренный треугольник и его свойства

Другие материалы

• 22.10.2020
• 186
• 7

• 20.10.2020
• 144
• 6

• 04.04.2020
• 955
• 52

• 04.04.2020
• 5318
• 78

• 04.04.2020
• 362
• 6

• 15.03.2020
• 1326
• 117

• 17.02.2020
• 232
• 3

• 16.01.2020
• 262
• 15

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 27.10.2020 761
• RAR 2.1 мбайт
• 55 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Малова Наталия Петровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 10 месяцев
• Подписчики: 0
• Всего просмотров: 2672
• Всего материалов: 4

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России планируют создадут сеть центров для подростков «группы риска»

Время чтения: 1 минута

Школьники Ленобласти уйдут на внеплановые каникулы

Время чтения: 1 минута

Новые курсы: школьные службы примирения, детская журналистика и другие

Время чтения: 15 минут

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

В Томске студентов вузов перевели на дистанционное обучение до конца февраля

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Правильный треугольник — свойства, признаки и формулы

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Общие сведения

Любое пространство можно описать размерностью. В трёхмерном измерении плоская геометрическая фигура, состоящая из трёх отрезков и такого же количества точек, в которых они соединяются, называется треугольником. Отрезки называют сторонами или боковыми гранями, площадь, ограниченная ими — внутренней, а точки — вершинами. Фигура имеет 3 угла и является невырожденной.

Строгого требования к обозначениям элементов многоугольника нет. Но традиционно вершины подписывают заглавными буквами латинского алфавита A, B, C, а противолежащие им стороны — аналогичными строчными знаками. В качестве обозначений для углов используют греческие символы: α, β, γ. Например, если имеется треугольник ABC, у него будут углы A, B, C и стороны a, b, c. Боковые грани могут подписываться и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA.

В зависимости от соотношения размеров сторон, все треугольники разделяют на 3 вида. Они бывают:

1. Равнобедренными — многоугольники, у которых одна сторона не равна двум другим. Эта грань называется основанием. Углы при этой стороне равны.
2. Разносторонние (неправильные) — длины всех граней разные.
3. Равносторонние — треугольники, имеющие одинаковые стороны. Часто эти фигуры называют правильными. По сути, они являются частным случаем равнобедренного многоугольника.

Существуют правила, позволяющие утверждать о равенстве или подобии двух и более треугольников. Они считаются идентичными, то есть их параметры полностью совпадают, если 2 стороны и угол равны или все грани имеют одинаковую длину. А также фигуры будут одинаковыми, когда у них совпадают 2 стороны и угол, располагающийся напротив большего отрезка.

Признаки подобия помогают определить вид треугольника при сравнении с известным. Если 2 любых угла равны в обеих фигурах, они считаются похожими. Когда же 2 стороны многоугольника пропорциональны двум отрезкам другого, причём углы, заключённые между этими гранями, равны, такие фигуры подобны.

Видео:7 фактов про равносторонний треугольникСкачать

Особые линии и точки

Медиана, высота и биссектриса — 3 замечательные линии любого треугольника. Представляют они собой внутренние отрезки, построенные из углов на противоположные стороны. Линия, соединяющая вершину с серединой противоположной грани, называется медианой. Луч, разделяющий угол на 2 равные части — это биссектриса, а перпендикуляр, построенный к стороне — высота.

В любом правильном треугольнике можно начертить 3 отрезка. Если отложить медиану, а потом биссектрису и высоту, можно заметить, что эти линии совпадут. Эта особенность и есть замечательным свойством равностороннего многоугольника, то есть если в любой другой трёхугольной фигуре можно построить 12 особых линий, то в рассматриваемом только 3.

Доказать это утверждение можно следующим образом: пусть имеется треугольник АВС, в котором проведена высота ВH. Далее, рассуждения нужно построить так:

1. Отрезок BH перпендикулярен прямой AC по построению.
2. Точка H разделяет отрезок AC на AD и CD. Если это утверждение будет верным, это означает, что построенная высота BH будет медианой треугольника.
3. Отрезок BH создаёт в многоугольнике 2 угла — ∠ABH и ∠CBH. При верности этого утверждения можно утверждать, что отрезок BH является биссектрисой.

Если создать зеркальное отражение треугольнику и совместить его с оригинальным, все углы попарно совместятся. Совпадут и стороны. Так как ВH — высота, она перпендикуляр. Значит, в точке H отрезок образует прямой угол с боковой гранью AC. Отсюда следует, что образованные треугольники AHB и CBH прямоугольные.

Они являются равными по общей гипотенузе и острому углу. Это следует из того, что правильный многоугольник — частный случай равнобедренного. Так как треугольники совпадают, у них одинаковые углы ABH и CBH. Причём они смежные, поэтому BH — биссектриса. В то же время точка H делит AC на 2 равных отрезка, значит, BH — медиана.

Точка, в которой пересекаются отрезки, будет центром тяжести фигуры. Её особенность в том, что она разделяет эту линию на 2 части в отношении 2 к 1, если считать от угла. Кроме этого, из-за равенства медианы и биссектрисы эта точка будет и ортоцентром.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

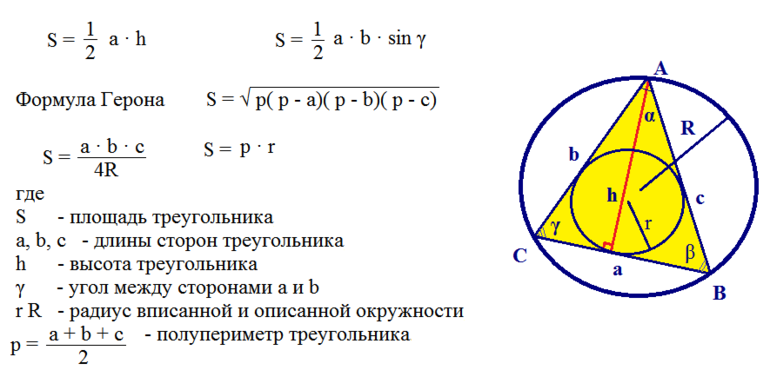
Основные формулы

Для каждого треугольника существует набор формул, с помощью которых можно определить его элементы. Чаще всего приходится выяснять длины сторон, площадь, высоты и периметр. При этом если известны боковые грани, можно найти практически любые остальные параметры.

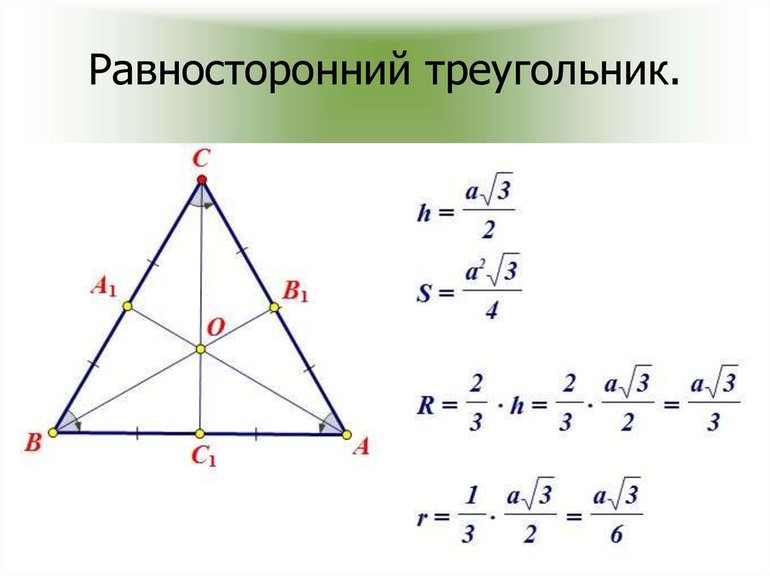
Вокруг правильной фигуры можно описать круг, причём окружность можно и вписать в середину. Что интересно, их центры совпадут между собой и с местом пересечения высот. В этом случае радиус внешнего круга равняется R = (a * √‎3) / 3 = a / 2 * sin (a), а внутреннего: r = (a * √‎3) / 6 = R / 2. Чтобы найти высоту, зная радиус, используют выражение: h = (3 *R) / 2. Кроме этой формулы, довольно часто применяют равенство, связывающее сторону и перпендикуляр: h = (a * √‎3) / 2.

Доказательство верности формулы для нахождения радиуса вписанной окружности можно построить исходя из выражения, справедливого к равнобедренной фигуре: r = b / 2 √(‎(2 a — b) / (2 a + b)). Так как стороны равны, то a = b. Получается, что r = a / 2 √‎(2a — a) / (2a + a) = (a / 2) * √‎(1 / 3) = a / (2 * √‎3) = (a √‎3) / 6.

Чтобы определить длину стороны, нужно знать высоту и теорему Пифагора. Согласно ей, квадрат гипотенузы находится как сумма квадратов высоты и длины разделённого основания. Применяя теорему к правильной фигуре, можно записать: AB 2 = h 2 + (AB / 2) 2 . Это равенство решают следующим образом: AB 2 = h 2 + AB 2 / 2 2 . Выражение можно преобразовать в вид: (3a 2 / 4) = h 2 → a 2 = (4 * h 2 ) / 3 → a 2 = √‎((4 * h 2 ) / 3) → a = (2 * h) / √3.

Из других существующих формул можно перечислить те, что чаще всего применяют при решении примеров:

1. Площадь. Находят из выражения: S = (a 2 * √3) / 4. Вывести эту формулу довольно просто. Если взять за основу, что равенство для площади верно, то исходя из свойств фигуры можно записать: S = ½ * a 2 * sin 60 = ½ * a 2 * √3 / 2 = (√3 / 4) * a 2 . Что и следовало доказать.
2. Периметр. Чтобы его определить, нужно сложить длины всех сторон, но так как в правильной фигуре они равны, можно воспользоваться формулой: P = 3 * a.

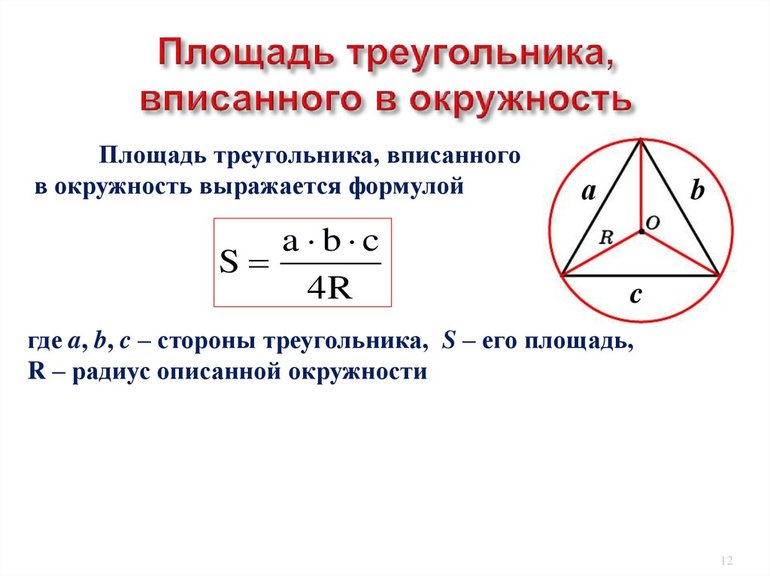
Существуют ещё 2 значимые теоремы: косинусов и синусов. Согласно первой, квадрат стороны фигуры будет ранятся удвоенному произведению двух оставшихся отрезков и косинусу угла между ними, отнятому из суммы квадратов: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Согласно же второй, длины отрезков пропорциональны синусам углов, лежащих напротив: a / sin (a) = b / sin (b) = c / sinс.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Решение задач

Чтобы уметь решать различные задания, связанные с треугольником, нужно помнить всего несколько формул. Но понадобится знать, что углы в фигуре равны друг другу и составляют 60 градусов. Часто придётся применять и теорему Пифагора. Вот некоторые из типовых заданий, используемые при обучении школьников в седьмом классе:

1. Какой будет радиус вписанной в правильный треугольник окружности, если его высота равняется 9 см. Зная свойство фигуры, решить задачу можно за пару секунд. Так как радиус равен 1/3 высоты, ответом на задачу будет: r = h / 3 = 9 / 3 = 3 см.
2. Сторона равностороннего треугольника равняется корню из трёх. Определить диаметр описанной окружности. Известно, что отношение синуса к противолежащему углу составляет 2R. Следовательно: R = a / 2 * sin (a) = √‎3 * 2 / 2 * √‎3 = 1.
3. Вокруг треугольной фигуры со стороной 8 √‎3 описан круг. Узнать его радиус. Эта задача в 2 действия. Используя формулу для нахождения вписанного радиуса и определение r = R / 2 можно записать: R = 2 * a * √‎3 / 6 = 2 * 8 * √‎3 * √‎3 / 6 = 2 * 4 = 8.
4. Пусть имеется квадрат, вокруг которого описана окружность. В ней так же располагается правильный треугольник. Периметр треугольной фигуры равен 9 √‎ 6. Нужно вычислить сумму всех сторон квадрата. На первом шаге необходимо определить длину боковой грани треугольника. Найти её можно по формуле: a = 3 √‎6. Теперь возможно рассчитать радиус описанной окружности: a = R * √‎3. Выполнив подстановку, найти ответ несложно: R = 3 √‎6 / √‎3 = 3 * √‎2. На третьем шаге можно выяснить, чему равняется сторона четырёхугольника. В этом поможет равенство: 3 √‎2 = (n √‎2) / 2. Отсюда n = 6. Значит, периметр квадрата равняется: P = 4 * 6 = 24.

Проверить правильность решения, возможно, используя онлайн-калькуляторы. Это сервисы, которые предлагают бесплатно вычислить элементы правильной фигуры. При этом от пользователя требуется лишь внести в специальную форму исходные данные и нажать кнопку «Рассчитать».

Следует отметить, что выучить наизусть все формулы сложно, поэтому обычно используют логическое мышление и теоремы синусов-косинусов. Учитывая, что любой угол в равностороннем треугольнике равен 60 градусов практически любую формулу вывести можно самостоятельно.

💥 Видео

7 класс. Геометрия. Равнобедренный треугольник. Равносторонний треугольник. Решение задачи. Урок #6Скачать

Признаки равенства треугольников. 7 класс.Скачать

МЕРЗЛЯК-7 ГЕОМЕТРИЯ РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК И ЕГО СВОЙСТВА ПАРАГРАФ-9Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Бестселлер Все правила по геометрии за 7 классСкачать

№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать

Треугольники. 7 класс.Скачать

Геометрия 7 класс - равнобедренный треугольник и его свойстваСкачать

№116. Докажите, что в равностороннем треугольнике все углы равны.Скачать