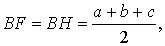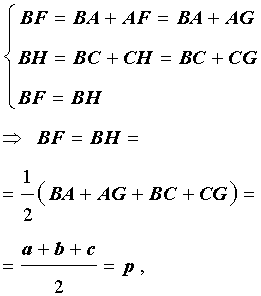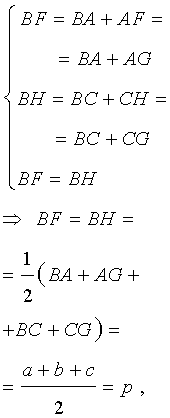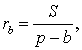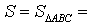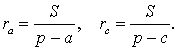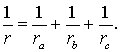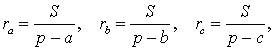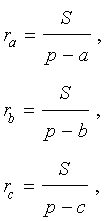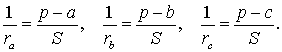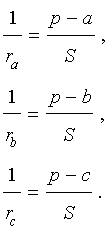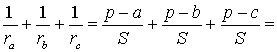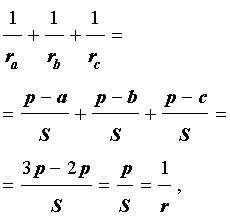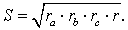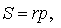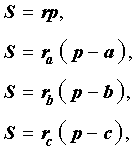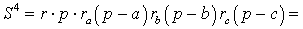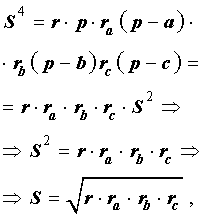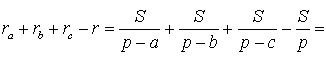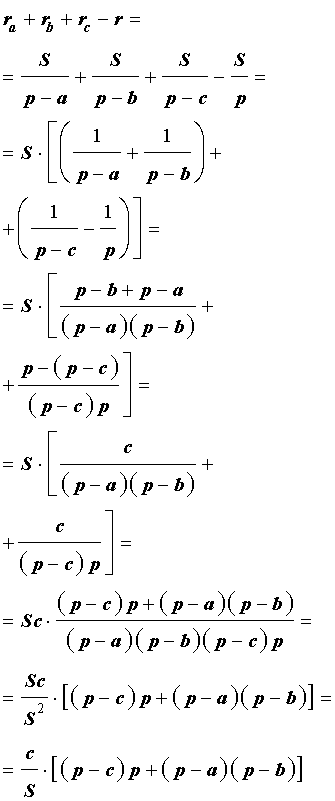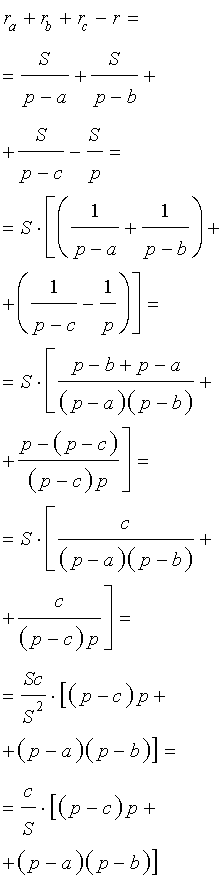Расстояние от вершины треугольника до точки касания вневписанной окружности

Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

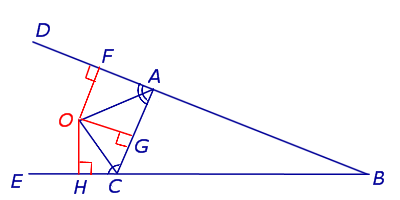
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

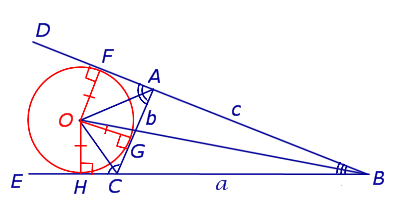
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом r_b .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

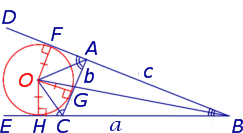
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

Следовательно, справедливо равенство

что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

,

что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

Доказательство . Перемножим формулы

что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

Преобразуем выражение, стоящее в квадратной скобке:

Видео:Треугольник. Расстояние от вершины до точки касания вневписанной окружности. Задание 16Скачать

Электронный сборник задач по теме » Вневписанная окружность»

Данная работа будетет интересна ученикам,желающим изучить теорию и научиться решать задачи на вневписанную окружность.Учителя могут применять данный материал при объяснении и отработке данной темы.

Видео:8 Расстояние от вершины треугольника до точек касания вписанной окружности со сторонамиСкачать

Скачать:

Предварительный просмотр:

Видео:✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

Подписи к слайдам:

Электронное пособие по теме : «Вневписанная окружность» .

Содержание: 1. Определение вневписанной окружности. Основные теоремы и формулы. Определение вневписанной окружности. Центр вневписанной окружности. Касательная к вневписанной окружности. Радиус вневписанной окружности: Соотношение между радиусом вневписанной окружности и периметром треугольника. Соотношение между радиусом вневписанной окружности, площадью и периметром треугольника. Задачи : Задача №1. Задача №2. Задача №3. 2. Соотношения с радиусами вневписанных окружностей. Выражение суммы радиусов вневписанных окружностей через радиус вписанной окружности и радиус описанной окружности. Выражение суммы величин, обратных радиусам вневписанных окружностей, через величину обратную радиусу вписанных окружностей. Выражение суммы всех попарных произведений радиусов вневписанных окружностей через квадрат полупериметра треугольника. Выражение произведения радиусов вневписанных окружностей через произведение радиуса вписанной окружности и квадрат полупериметра треугольника. + следствие №1. следствие №2. Задачи : Задача №4. Задача №5. Задача №6. Задача №7.

1. Определение вневписанной окружности. Основные теоремы и формулы.

Вневписанная окружность. Окружность называется вневписанной для треугольника, если она касается одной стороны треугольника и продолжений двух других сторон. Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных . О 3 O 2 О 1

Центр вневписанной окружности. Центр вневписанной окружности треугольника — точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника. . А В С O

Дано:  ABC ; Вневписанная окр. (О а ; r а ) Доказать: Док-во: Т.к. касательные, проведенные из одной точки, равны ,то ВВ 1 =ВА 1 , СА 1 =СС 1 , АВ 1 =АС 1 . Значит, P = (АС+СА 1 )+(АВ+ВА 1 )= (АС+СС 1 )+(АВ+ВВ 1 )= АС 1 +АВ 1 =2АС 1 =2АВ 1 , т.е. Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника

Дано:  ABC ; Вневписанная окр. (О а ; r а ) Доказать: Док-во: В прямоугольном треугольнике  АО а С 1 r a и – длины катетов, О а АС = , поэтому , что и требовалось доказать. II . Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е.

III . Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. т.е. Дано:  ABC ; Вневписанная окр. (О а ; r а ) Доказать: Док-во: Имеем: , что и требовалось доказать. А В С О а В 1 С 1 b c r a r a r a а

Задачи на свойства касательной к вневписанной окружности и ее радиусов:

Задача№1. Найдите периметр треугольника АВС, если расстояние от вершины А до точки касания с вневписанной окружностью равно 17 , расстояние от вершины B до точки касания окружности со стороной BC равно 6, расстояние от вершины С до точки касания окружности со стороной АC равно 4. (авторская задача) Решение

Решение №2: 1) Т.к АВ 1 = АС 1 = ( по теореме о касательной вневписанной окружности) , то Р= АВ 1 * 2 => Р= 17*2=34. Ответ: Р = 34. Решение: Дано: Окр(О а ;О а C 1 );  АВС;AB 1 =17, BL =6, CC 1 =4. Найти: P -?. Решение №1: 1) Рассмотрим  АВС. Т.к. BL=BB 1 =6 (как отрезки касательных, проведенные из одной точки), то АВ=АВ 1 — BB 1 => АВ =17-6 =11 . 17 А В В 1 О а L 6 4 С С 1 2) Т.к. СL=СB 1 =4 (как отрезки касательных, проведенные из одной точки), то ВС=BL + LC => В C =6+4 =10 . 4) Р=AB+ВС+АС => Р=11+10+13=34 . 3) Т.к. AB 1 =АС 1 =17 (как отрезки касательных, проведенные из одной точки), то АС= АС 1 — CC 1 => АС =17-4 =13 . 13

Задача№2. Решение Задача№2. Найдите радиус вневписанной окружности треугольника со сторонами 13, 13, 10. ( ЕГЭ- 2015, система задач по геометрии Р.К.Гордина)

Решение 1 : Дано: Окр(О а ; r а );  АВС;AB=1 3 , AC = 13 , BC=10 . Найти: r а -?. Решение (1 случай) : 1 . Пусть стороны AB , AC и BC треугольника ABC равны 13, 13 и 10 соответственно, AH — высота треугольника, r a — радиус вневписанной окружности, касающейся сторон BC , AC и AB — в точках H , K и M соответственно. А В С M H О а r a 5 5 5 13 13 12 18 K 2.Поскольку  АВС равнобедренный, точка H — высота и середина основания BC. Рассмотрим  А H В, где  H=90  . По теореме Пифагора: 3. Пусть O a — центр вневписанной окружности, касающейся стороны BC и продолжения сторон AC и AB, причём продолжения стороны AB —в точке M. Тогда BM = BH = 5 (как отрезки касательных, проведенные из одной точки) ; AM = AB + BM = 13 + 5 = 18. 4. Рассмотрим  А MO a , где  M=90  (т еорема о касательной к окружности ). По теореме радиусе вневписанной окружности получаем, что ( AM= по теореме о расстоянии от вершины угла треугольника до точек касания с вневписанной окружности )

Решение 2 : Дано: Окр(О c ; r c );  АВС;AB=1 3 , AC = 13 , BC=10 . Найти: r c -?. Решение (2 случай): 1 . Пусть O c — центр вневписанной окружности, касающейся стороны AB и продолжений сторон BC и AC в точках K и L соответственно. Тогда AO —биссектриса  BAL, а так как AH — биссектриса смежного с ним  BAC, то ∠ HAO c = 90  . А В С L H О c r c 5 5 13 12 K 2. Четырёхугольник AO c KH — прямоугольник (∠ HAO c = ∠AHK = ∠HKO c = 90  ), поэтому r c = O c K = AH = 12 . 3. Аналогично найдём, что r b = AH = 12. Ответ: r a = 7,5; r b = 12 ; r c = 12 . 12

Задача№3. Найдите радиус вневписанной окружности, если расстояние от вершины А до точки касания с окружностью равно 21, BC=15, AB=14,AC=13. (авторская задача) Решение

Дано: AB 1 =21, AB=14, AC=13, BC=15. Найти: r a -? . Решение : O A C C 1 L 1 5 1 3 B 21 1 4 B 1 1 ) Рассмотрим  ABC : 2 ) 3) По теореме о радиусе вневписанной окружности:  ( по формуле Герона) ( по теореме о касательной к вневписанной окружности) Ответ: r a = 14 . r a r a Решение:

2. Соотношения с радиусами вневписанных окружностей.

Выражение суммы радиусов вневписанных окружностей через радиус вписанной окружности и радиус описанной окружности . Дано:  ABC ; Вневписанная окр. (О а ; r а ), (О b ; r b ), (О c ; r c ), вписанная окр .(О; r ), описанная окр.(О; R). Доказать: Док-во: Выразим все радиусы через стороны, S и полупериметр треугольника: Значит,  поскольку радиус описанной окружности удовлетворяет равенству , то справедлива формула ,что и требовалось доказать. О c О b О a О О r c r b r a r R a b c

Выражение суммы величин , обратных радиусам вневписанных окружностей , через величину обратную радиусу вписанных окружностей . Выражение суммы всех попарных произведений радиусов вневписанных окружностей через квадрат полупериметра треугольника.

Выражение произведения радиусов вневписанных окружностей через произведение радиуса вписанной окружности и квадрат полупериметра треугольника . Дано:  ABC ; Вневписанная окр. (О а ; r а ), (О b ; r b ), (О c ; r c ) , вписанная окр.(О; r). Доказать: Док-во: Из ранее доказанных формул для радиусов и формулы Герона Тогда , что и требовалось доказать. Следствия r a r c r b О c О b О а В A r C О

1 следствие: Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника. Дано:  ABC ; Вневписанная окр. (Оа; r а ), (О b ; r b ), (О c ; r c ) . Доказать: Док-во : Из Следовательно , что и требовалось доказать. О c r c В r a О а C r b О b A

2 следствие: Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности. Дано:  ABC ; Вневписанная окр. (Оа; r а ), (О b ; r b ), (О c ; r c ) вписанная окр.(О; r). Доказать: Док-во : Из следствия 1 , что и равенства, получаем, перемножая их почленно, . Значит, , что и требовалось доказать. О c r c В r a О а C r b О b A О r

Задачи на соотношения с радиусов вневписанных окружностей:

Задачи: Задача№4. Найдите радиус вневписанной окружности треугольника, если радиусы двух других вневписанных окружностей равны 2002 и 4004, а радиус вписанной окружности равен 1001. Решение

Решение: Дано:  ABC ; Окр(О; r х =1001), Окр(О 3 , r с ), Окр(О 1 ; r а =2002), Окр(О 2 ;r b =4004). Найти: r с -? O 3 O 2 O O 1 r a r c r b r x 2002 1001 4004 ? C A В Т.к. сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, а именно , то c оставим равенство: Ответ: r с =4004 . Решение:

Задачи: Задача №5. Найдите произведение сторон треугольника, если известно, что радиусы его вневписанных окружностей равны 9,18 и 21. (сборник «Подготовка к ЕГЭ -2010, под редакцией Ф.Ф.Лысенко) Решение

Решение: Дано:  ABC ; r a =9, r b =18, r c =21 ; Окр(О, r с ), Окр(О; r а ), Окр(О; r b), Окр(О; R ) . Найти: , следовательно r a r b r c O O O O R r О 1. Найдем S : , получаем 2. Найдем 4 R : Подставляем: Ответ: 5460. Решение:

Задачи: Задача №6. Найдите произведение радиусов всех вневписанных окружностей треугольника со сторонами 4,5,6. (сборник «Подготовка к ЕГЭ- 2010, под редакцией Ф.Ф.Лысенко) Решение

Решение: Дано:  ABC ; a= 4 , b= 5 , c= 6; Окр(О, r с ), Окр(О; r а ), Окр(О; r b) Найти: 2. Так как , то Таким образом, Ответ: a (4) c (6) b (5) O O O r a r b r c O r 1. Так как , где r -радиус вписанной в треугольник окружности, то: Решение:

Задачи: Задача№7. Основание АС равнобедренного треугольника равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности вписанной в треугольник АВС. (сборник «Подготовка к ГИА -2013, под редакцией Д.А. Мальцева) Решение

3. АК – высота, проведенная к гипотенузе  AK²=FK*KO ( по теореме о высоте прямоугольного )  Так как FK – радиус вписанной в  АВС окружности, следовательно Ответ: Решение: Дано:  ABC -равнобедренный; AC = 10; вписанная окр.( F ; r), вневписанная о кр.(О; r а= 7,5 ). Найти: r- ? 1 . Так как окружность касается стороны треугольника и продолжения двух других сторон, то это — вневписанная окружность. F O А B C K r r a 2. Так как центр вписанной окружности и вневписанной окружности лежит в точке пересечения биссектрис, то AF-биссектриса  ВАС, а AO – биссектриса  CAD   FAO – прямоугольный треугольник, так как биссектрисы смежных углов образуют прямой угол. D Решение:

Видео:ВСЕ свойства ортоцентра для №16 на ЕГЭ 2023 по математикеСкачать

Please wait.

Видео:Вневписанная окружностьСкачать

We are checking your browser. mathvox.ru

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Вневписанная окружностьСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d9401ba3bb775af • Your IP : 85.95.188.35 • Performance & security by Cloudflare

🔥 Видео

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

11.51.1. Планиметрия. Гордин Р.К.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Задание 26 Вневписанная окружностьСкачать

Разбор Задачи №16 из Варианта Ларина №282Скачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Это будет на ЕГЭ 2020 по математике. Вписанная и вневписанная окружности.Скачать

Вписанные, описанные, вневписанные окружностиСкачать

Математика ОГЭ Задание 26 Вневписанная окружностьСкачать

Разбор задачи 16 про вневписанные окружности. Геометрия. ЕГЭ 2019Скачать

Калитки. Лайфхак для вписанных и вневписанных окружностейСкачать

ЕГЭ 2021 Математика. Метод площадей. Теорема Чевы. Вневписанная окружностьСкачать