Расстояние между центрами вписанной и описанной окружности треугольника доказательство

Формула Эйлера

Мы знаем, что в каждый треугольник можно вписать окружность и можно описать около него окружность. Ясно, что вписанная окружность лежит внутри описанной, поскольку вписанная окружность лежит внутри треугольника, а сам треугольник лежит внутри описанной окружности.

Радиусы вписанной и описанной окружностей и расстояние между их центрами всегда связаны между собой определенным соотношением. Справедлива следующая теорема.

Теорема. В треугольнике радиус R описанной окружности и радиус r вписанной окружности связаны с расстоянием d между их центрами соотношением

В частности, если d=0 (центры окружностей совпадают), то .

Эта формула называется формулой Эйлера.

Доказательство.

Рассмотрим треугольник АВС, у которого точка О – центр описанной окружности, а точка – центр вписанной окружности. Будем считать пока, что (рисунок 1). Проведем биссектрисы и углов А и В. Они пересекаются с описанной окружностью в некоторых точках и . Пусть P и Q – точки пересечения прямой с описанной окружностью. По теореме о произведении отрезков пересекающихся хорд , или

Заметим теперь, что поскольку и – биссектрисы углов А и В, то , а . Следовательно,

Поэтому треугольник равнобедренный: . Таким образом, соотношение можно переписать так:

Проведем теперь диаметр описанной окружности и обозначим буквой К точку касания вписанной окружности и стороны АВ. Треугольники и подобны (они прямоугольные и имеют равные углы А и ), поэтому

Откуда . Подставив это выражение, получим

В случае d=0 (рисунок 2) каждая из сторон треугольника АВС равна , а значит, этот треугольник равносторонний.

Поэтому , , и, следовательно, . Теорема доказана.

Замечание. В ходе доказательства теоремы мы установили весьма полезный факт:

Точка пересечения продолжения биссектрисы, проведенной из одной из вершин треугольника, с описанной окружностью равноудалена от двух других вершин и центра вписанной окружности.

Теорема Птолемея

В любой треугольник можно вписать окружность и около него можно описать окружность. Однако для других многоугольников это не так. Мы знаем, например, что в четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны. Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна . Эти утверждения очень похожи друг на друга. Используя скобки, их можно объединить в одно:

Описанная (вписанная) окружность для данного четырехугольника существует тогда и только тогда, когда суммы его противоположных углов (сторон) равны.

Существуют и другие характеристические свойства вписанных и описанных четырехугольников. Наиболее известное основано на теореме Птолемея.

Теорема (Птолемея). Произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений противоположных сторон.

Доказательство.

Рассмотрим вписанный четырехугольник АВСD. Для удобства введем обозначение: АВ = а, ВС = b, CD = c, DA = d, AC = m, BD = n (рисунок 3) и докажем, что .

На диагонали АС возьмем такую точку М, что . Треугольники АВМ и DBC подобны по двум углам ( по построению, а углы ВАМ и BDC равны как вписанные и опирающиеся на одну и ту же дугу). Следовательно, , откуда , или (1).

Далее, треугольники МВС и ADB также подобны, так как , а углы ВСМ и BDA равны как вписанные и опирающиеся на одну и ту же дугу. Поэтому , , откуда , или (2).

Сложив равенства (1) и (2), получим , или , что и требовалось доказать.

Оказывается, что рассмотренное свойство вписанного четырехугольника является характеристическим, то есть верно и обратное утверждение.

Если в выпуклом четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон, то около него можно описать окружность.

Рекомендую далее изучить тему «Вневписанные окружности».

Спасибо, что поделились статьей в социальных сетях

Источник: Атанасян Л.С. Геометрия. Дополнительные главы к учебнику 8 кл.: Учебное пособие для учащихся школ и классов с углубленным изучением математики.

Видео:М1152. Расстояние между центрами вписанной и описанной окружностейСкачать

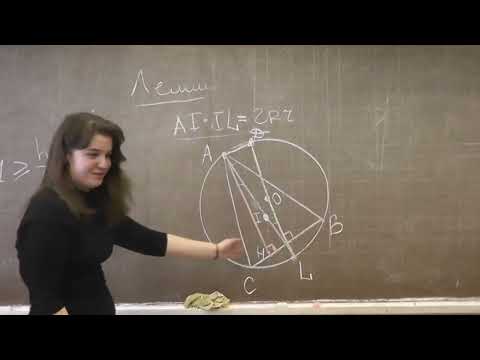
Формула Эйлера.

В треугольнике OI 2 =R 2 -2Rr , где I — точка пересечения биссектрис (центр вписанной окружности), O — центр описанной окружности, R — радиус описанной окружности, r — радиус вписанной окружности.

Доказательство:

Пусть AM — хорда описанной окружности, проходящая через точку I.

Тогда по теореме о пересекающихся хордах: AI·IM=(R+OI)(R-OI).

Из треугольника AIH по определению синуса: AI=r/sin(α/2).

Из треугольника MAC по теореме синусов и лемме о трезубце: CM=2Rsin(α/2)=IM.

Подставим полученные равенства в AI·IM=(R+OI)(R-OI):

r/sin(α/2)·2Rsin(α/2)= R 2 -OI 2

Следовательно, OI 2 =R 2 -2Rr.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Расстояние между центрами вписанной и описанной окружности треугольника доказательство

2021-11-23
Дан треугольник со сторонами 25, 25 и 48.
а) Докажите, что он тупоугольный.
б) Найдите расстояние между центрами его вписанной и описанной окружностей.

а) Пусть $AB=AC=25$, $BC=48$ — стороны треугольника $ABC$ (рис.1). По теореме косинусов

Следовательно, $angle BACgt180^$.
б) Пусть $AH$ — высота равнобедренного треугольника $ABC$ (рис.2). Тогда $H$ — середина $BC$, а т.к. $AH$ — биссектриса треугольника, то центр $O_$ вписанной окружности лежит на отрезке $OH$. Поскольку треугольник $ABC$ тупоугольный с тупым углом при вершине $A$, центр $O$ его описанной окружности и вершина $A$ лежат по разные стороны от прямой $BC$, причём точка $O$ лежит на серединном перпендикуляре к стороне $BC$, т.е. на прямой $AH$. Значит, $OO_=OA-O_A$.
Из прямоугольного треугольника $AHB$ находим, что

Пусть $OA=R$ — радиус описанной окружности треугольника $ABC$. По теореме синусов

Пусть $S$ — площадь треугольника $ABC$, $p$ — полупериметр, $r=O_H$ — радиус вписанной окружности. Тогда

📹 Видео

Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать

7 9 2011 М1152 формула Эйлера расстояния между центрами вписанной и описанной окружностейСкачать

Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Планиметрия 11 |mathus.ru|  расстояние между центрами пересекающихся окружностейСкачать

Вписанная окружность. Доказательства свойствСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Геометрия 6. Радиусы вписанной и описанной окружностей.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Задача о треугольнике из тренировочного варианта ЕГЭСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать