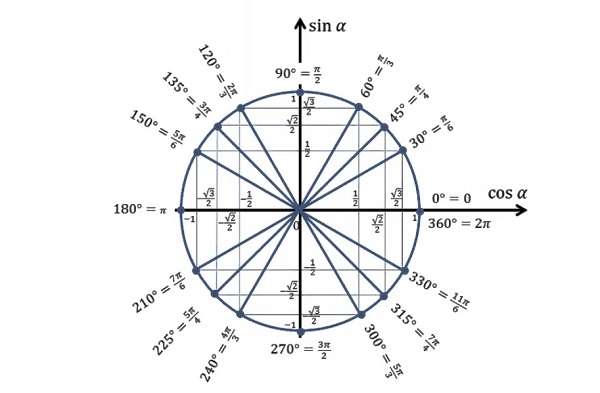
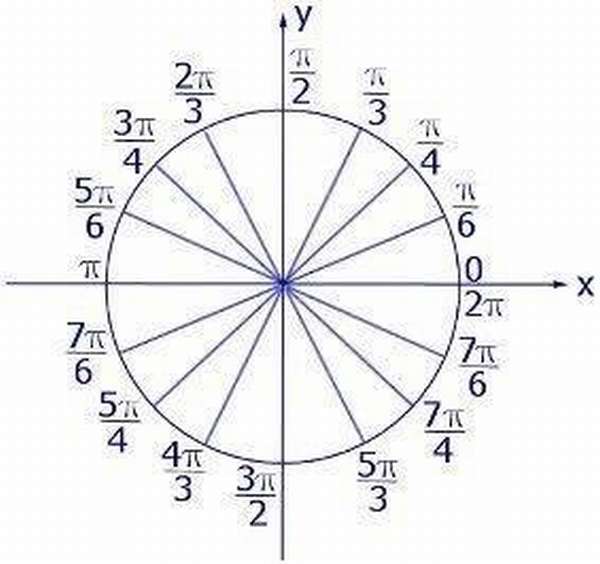
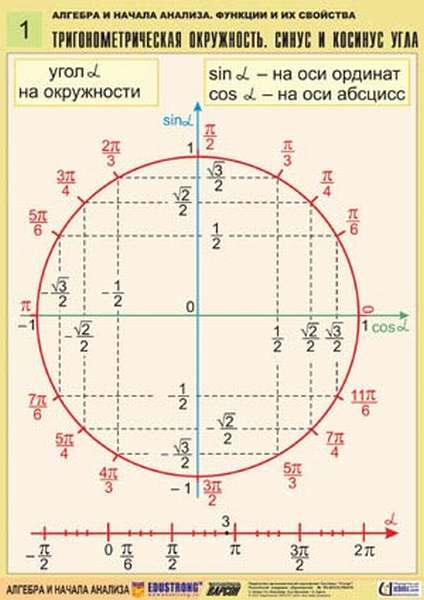
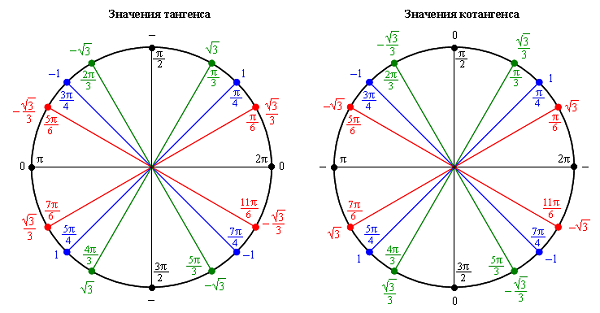
Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
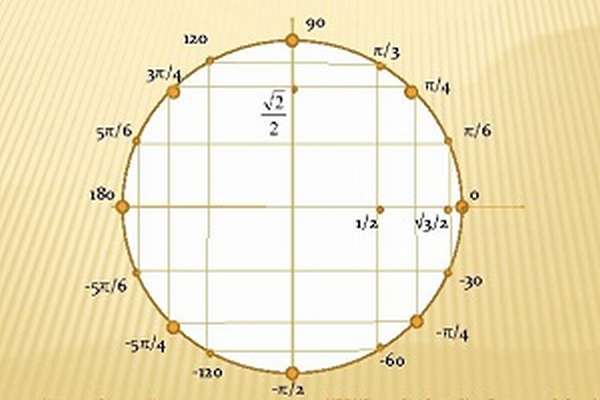
- Тригонометрический круг: вся тригонометрия на одном рисунке
- А теперь подробно о тригонометрическом круге:
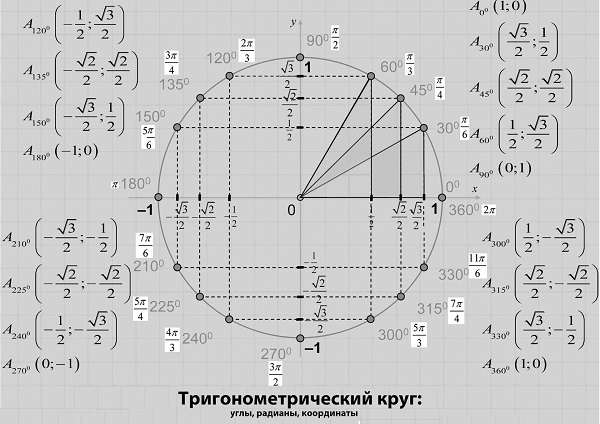
- Тригонометрический круг со всеми значениями
- Тригонометрическая окружность
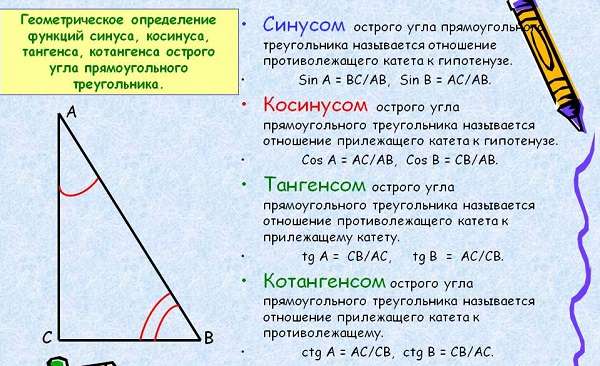
- Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
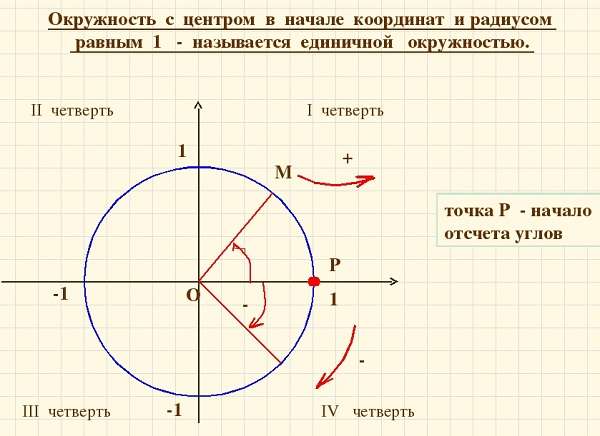
- Построение единичной окружности
- Углы на тригонометрическом круге
- Перевод углов из градусов в радианы
- Косинус, синус, тангенс, котангенс на тригонометрической окружности
- Заключение
- 🔍 Видео
Видео:Как искать точки на тригонометрической окружности.Скачать

Почему так важно определять какой четверти принадлежит угол?
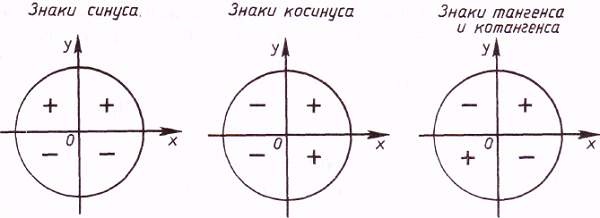
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
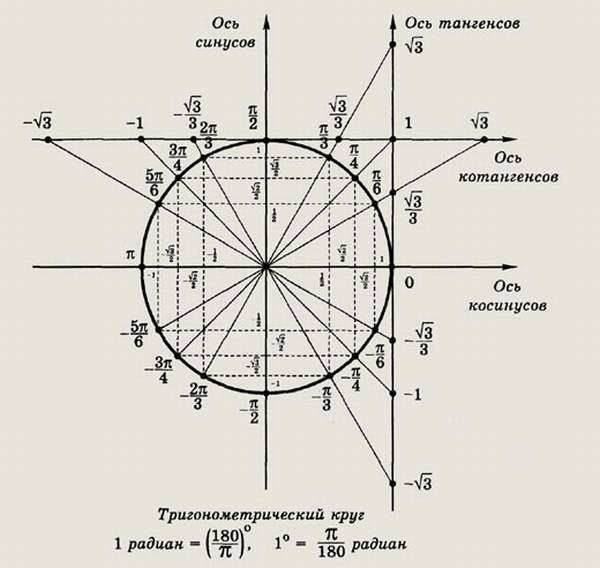
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Тригонометрическая окружность. Как выучить?Скачать  Тригонометрический круг: вся тригонометрия на одном рисункеТригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Вот что мы видим на этом рисунке: Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  А теперь подробно о тригонометрическом круге:Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций. Мы отсчитываем углы от положительного направления оси против часовой стрелки. Полный круг — градусов. Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу . Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу . Всё это легко увидеть на нашем рисунке. Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до : Простым следствием теоремы Пифагора является основное тригонометрическое тождество: Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ). Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы. Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке. Легко заметить, что Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть: где — целое число. То же самое можно записать в радианах: Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению, Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  Тригонометрический круг со всеми значениями Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом. Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее. Видео:Длина окружности. Площадь круга. 6 класс.Скачать  Тригонометрическая окружностьТригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат. Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям. Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольникеПрямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов. Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение. Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать  Построение единичной окружностиПостроение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты. Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами. Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга. Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать  Углы на тригонометрическом кругеДля того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто. Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией? Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними. Измеряются углы в радианах:
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке. Видео:Как найти координаты точек на тригонометрической окружностиСкачать  Перевод углов из градусов в радианыУглы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно. Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой: 1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956 В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан: 1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад. Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать  Косинус, синус, тангенс, котангенс на тригонометрической окружностиКосинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге. Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  ЗаключениеВ целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач. 🔍 ВидеоСоответствие чисел точкам числовой окружностиСкачать  Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать  Числовая окружностьСкачать  Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать  1. Числовая окружность. 10 классСкачать  ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать  46 Где расположены на единичной окружности точки π/3,π/6 и другиеСкачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  |