Если у шестиугольника как углы, так и стороны равны, соответственно, это — правильный многоугольник, вокруг которого можно описать лишь одну окружность. Все вершины шестиугольника лежат на описанной вокруг него окружности. У правильного шестиугольника центр расположен на равном расстоянии от его вершин. Центр шестиугольника и центр описанной окружности совпадают. Линия, которая соединяет центр с вершинами, считается радиусом как многоугольника, так и описанной окружности. В правильном шестиугольнике сторона и радиус равны. Отсюда, R описанной окружности равняется его стороне или диагонали, поделенной пополам:
В данном выражении:
а — величина стороны шестиугольника;
R — величина радиуса;
d — диагональ.
Онлайн калькулятор поможет быстро и правильно найти величину радиуса, для этого вам нужно лишь занести исходные данные.
Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

ГОСТ 8560-78
ПРОКАТ КАЛИБРОВАННЫЙ ШЕСТИГРАННЫЙ.
СОРТАМЕНТ
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРОКАТ КАЛИБРОВАННЫЙ ШЕСТИГРАННЫЙ. СОРТАМЕНТ
Rolled-stock calibrated hexahedronal. Range of products.
Взамен
ГОСТ 8560-67
Ограничение срока действия снято по протоколу № 7-95 Межгосударственного Совета по стандартизации, метрологии и сертификации (ИУС 11-95)
1. Настоящий стандарт распространяется на прокат калиброванный шестигранный размером от 3 до 100 мм.
Стандарт полностью соответствует рекомендации СЭВ РС 962-67.
(Измененная редакция, Изм. № 2).
2. Размеры сечения проката и предельные отклонения по ним в зависимости от классов точности должны соответствовать указанным на чертеже 1 и в табл. 1.
| Размер проката (диаметр аписанного круга а или размер «под ключ»), мм | Предельные отклонения, мм | Диаметр описанной окружности, А, мм | Предельные отклонения, мм | Площадь поперечного сечения, мм2 | Масса 1 м длины, кг | ||
| h10 | h11 | h12 | |||||
| 3,0 | -0,040 | -0,060 | -0,100 | 3,4 | -0,2 | 7,79 | 0,061 |
| 3,2 | -0,048 | -0,075 | -0,120 | 3,7 | 8,87 | 0,070 | |
| 3,5 | 4,0 | 10,61 | 0,083 | ||||
| 4,0 | 4,6 | 13,86 | 0,109 | ||||
| 4,5 | 5,2 | 17,54 | 0,138 | ||||
| 5,0 | 5,8 | 21,65 | 0,170 | ||||
| 5,5 | 6,3 | 26,20 | 0,206 | ||||
| 6,0 | 6,9 | 31,18 | 0,245 | ||||
| 6,5 | -0,058 | -0,090 | -0,150 | 7,4 | 36,59 | 0,2087 | |
| 7,0 | 8,1 | 42,44 | 0,333 | ||||
| 8,0 | 9,2 | -0,4 | 55,43 | 0,435 | |||
| 9,0 | 10,4 | -0,5 | 70,15 | 0,551 | |||
| 10,0 | 11,5 | 86,60 | 0,608 | ||||
| 11,0 | -0,070 | -0,110 | -0,180 | 12,7 | -0,6 | 104,8 | 0,823 |
| 12,0 | 13,8 | 124,7 | 0,979 | ||||
| 13,0 | 15,0 | -0,7 | 146,4 | 1,150 | |||
| 14,0 | 16,2 | 169,7 | 1,330 | ||||
| 15,0 | 17,3 | 194,9 | 1,530 | ||||
| 16,0 | 18,4 | 221,7 | 1,740 | ||||
| 17,0 | 19,6 | -0,8 | 250,3 | 1,960 | |||
| 18,0 | 20,7 | 280,6 | 2,200 | ||||
| 19,0 | -0,084 | -0,130 | -0,210 | 21,9 | 312,6 | 2,450 | |
| 20,0 | 23,0 | 346,4 | 2,720 | ||||
| 20,8 | 23,9 | -0,9 | 274,7 | 2,940 | |||
| 21,0 | 24,2 | 381,9 | 3,000 | ||||
| 22,0 | 25,4 | 419,2 | 3,290 | ||||
| 24,0 | 27,7 | 498,8 | 3,920 | ||||
| 25,0 | 28,8 | 541,3 | 4,250 | ||||
| 26,0 | 30,0 | -1,0 | 585,4 | 4,600 | |||
| 27,0 | 31,2 | 631,3 | 4,960 | ||||
| 28,0 | 32,3 | 679,0 | 5,330 | ||||
| 30,0 | 34,6 | 779,4 | 6,120 | ||||
| 32,0 | -0,100 | -0,160 | -0,250 | 36,9 | -1,1 | 886,8 | 6,96 |
| 34,0 | 39,2 | 1001,0 | 7,86 | ||||
| 36,0 | 41,6 | -1,3 | 1122,0 | 8,81 | |||
| 38,0 | 43,8 | 1251,0 | 9,82 | ||||
| 40,0 | 46,1 | 1386,0 | 10,88 | ||||
| 41,0 | 47,3 | 1456,0 | 11,40 | ||||
| 42,0 | 48,5 | 1527,0 | 11,99 | ||||
| 45,0 | 51,9 | 1754,0 | 13,77 | ||||
| 46,0 | 53,1 | -1,4 | 1833,0 | 14,40 | |||
| 48,0 | 55,4 | -1,5 | 2000,0 | 15,60 | |||
| 50,0 | 57,7 | 2165,0 | 17,00 | ||||
| 53,0 | -0,120 | -,0190 | -0,300 | 61,2 | -1,7 | 2433,0 | 19,1 |
| 55,0 | 63,5 | 2620,0 | 20,6 | ||||
| 56,0 | 64,6 | 2715,0 | 21,3 | ||||
| 60,0 | 69,3 | 3118,0 | 24,5 | ||||
| 63,0 | 72,7 | 3437,0 | 27,0 | ||||
| 65,0 | 75,0 | -1,8 | 3659,0 | 28,7 | |||
| 70,0 | — | -0,190 | -0,300 | 80,8 | 4244,0 | 33,3 | |
| 75,0 | 86,5 | -1,9 | 4871,0 | 38,2 | |||
| 80,0 | 92,3 | 5542,0 | 43,5 | ||||
| 85,0 | — | -0,220 | -0,350 | 98,0 | -1,2 | 6257,0 | 49,1 |
| 90,0 | 104,0 | -1,3 | 7015,0 | 55,1 | |||
| 95,0 | 110,0 | 7816,0 | 61,4 | ||||
| 100,0 | 115,0 | -1,4 | 8660,0 | 68,0 | |||
1. По требованию потребителя прокат калиброванный шестигранный изготовляют других размеров, не указанных в табл.1. Предельные отклонения в этом случае должны соответствовать нормам, установленным для ближайшего большего диаметра.
2. Площадь поперечного сечения и линейная плотность проката калиброванного шестигранного вычислены по номинальному размеру. Плотность проката принята равной — 7,85 г/см3.
3. Для проката из высоколегированных марок сталей и сплавов, подвергаемых термической обработке и травлению, предельные отклонения по размерам устанавливаются на 30 % более квалитета h12.
(Измененная редакция, Изм. № 1, № 2).
3. Прокат калиброванный шестигранный изготовляется в прутках. По требованию потребителя прокат изготовляется в мотках.
4. В зависимости от назначения прутки изготовляют:
кратной мерной длины;
немерной длины с остатком до 10 % массы партии;
ограниченной длины в пределах немерной.
Остатком считаются прутки длиной не менее 1,5 м.
(Измененная редакция, Изм. № 1).
5. Прутки изготовляют длиной от 2 до 6,5 м. По требованию потребителя прутки изготавливаются больших длин.
3-5 (Измененная редакция, Изм. № 1).
Пункты 6, 7 исключены, Изм. № 1).
8. Предельные отклонения по длине прутков мерной и кратной мерной длины не должны превышать:
+30 мм — при длине прутков до 4 м;
+50 мм — при длине прутков свыше 4 м.
9. Кривизна прутков не должна превышать значений, указанных в табл.2
| Размер прутков, мм | Предельная кривизна в зависимости от поля допуска | |||
| на 1 м длины, мм | на полную длину, % | |||
| h10 и h11 | h12 | h10 и h11 | h12 | |
| До 25 | 2 | 3 | 0,2 | 0,3 |
| Св. 25 до 50 | 1 | 2 | 0,1 | 0,2 |
| Св. 50 | 1 | 1 | 0,1 | 0,1 |
Отклонение от прямолинейности должно быть равномерным по всей длине. На концах прутков короткие продольные изгибы не допускаются.
(10. Скручивание прутков на 1 м длины (черт.2) не должно превышать 3°.
11. Рез прутка должен быть под прямым углом к его продольной оси. Допускаемая косина реза не должна превышать:
0,2 а — при размере прутков до 15мм;
0,17 а — при размере прутков до 16 мм;
3 мм — при размере прутков свыше 16 до 30 мм.
5мм-при размере прутков свыше 30 мм
9-11 (Измененная редакция, Изм. № 1).
12. Длина смятых концов прутков не должна превышать норм, указанных в табл.3.
| Размер прутков | Длина смятых концов, не более |
| До 25 | 20 |
| Св. 25 до 50 | 25 |
| » 50 » 70 | 30 |
(Введен дополнительно, Изм. № 1).
13. Радиус закругления кромок определяется по требованию потребителя и не должен превышать, значений, указанных в табл.4.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Шестигранник вписанный в окружность формулы
Если у шестиугольника как углы, так и стороны равны, соответственно, это — правильный многоугольник, вокруг которого можно описать лишь одну окружность. Все вершины шестиугольника лежат на описанной вокруг него окружности. У правильного шестиугольника центр расположен на равном расстоянии от его вершин. Центр шестиугольника и центр описанной окружности совпадают. Линия, которая соединяет центр с вершинами, считается радиусом как многоугольника, так и описанной окружности. В правильном шестиугольнике сторона и радиус равны. Отсюда, R описанной окружности равняется его стороне или диагонали, поделенной пополам:
В данном выражении:
а — величина стороны шестиугольника;
R — величина радиуса;
d — диагональ.
Онлайн калькулятор поможет быстро и правильно найти величину радиуса, для этого вам нужно лишь занести исходные данные.

Видео:Периметр правильного шестиугольника равен 222. Найдите диаметр описанной окружности.Скачать

Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Свойства простые и интересные
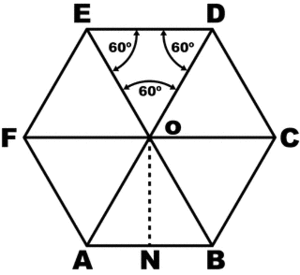
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
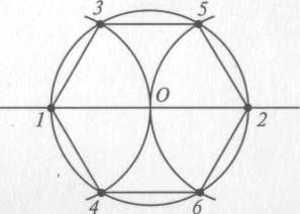
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
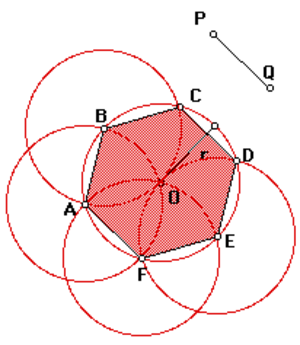
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
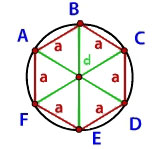
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

От теории к практике
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Обучающее видео
БЕСПЛАТНО
Техническая поддержка:
dvd@ege-study.ru (круглосуточно)
Полный онлайн-курс подготовки к ЕГЭ по математике. Структурировано. Четко. Без воды. Сдай ЕГЭ на 100 баллов!
Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.
Все поля обязательны для заполнения
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Премиум
Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.
Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса – от 3,5 до 4,5 часов.
- Уравнения (задача 13)
- Стереометрия (задача 14)
- Неравенства (задача 15)
- Геометрия (задача 16)
- Финансовая математика (задача 17)
- Параметры (задача 18)
- Нестандартная задача на числа и их свойства (задача 19).
Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.
Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум – репетитор-профессионал Анна Малкова.
Видео:151 Диагонали правильного шестиугольника пересекаются в центре его описанной окружности (268)Скачать

Получи пятерку
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля – до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.
Задачи комплекта «Математические тренинги – 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.
Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Как пользоваться?
- Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
- Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
- Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
- Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
- Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.
Стоимость комплекта «Математические тренинги – 2019» – всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.
🎥 Видео
112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Геометрия - Построение шестиугольникаСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Радиус описанной окружностиСкачать

Свойства правильного шестиугольника. Сравнение площадей. Разбор задачи из стереометрии.Скачать

Как построить правильный шестиугольник.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Геометрия 9 класс (Урок№26 - Построение правильных многоугольников.)Скачать

Размеры шестигранникаСкачать

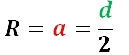


 чертится прямая линия и на ней ставится точка;
чертится прямая линия и на ней ставится точка;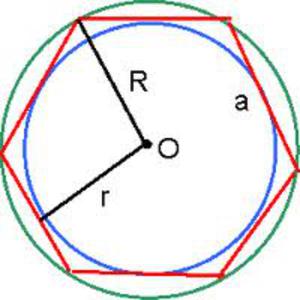 Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.



