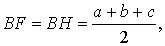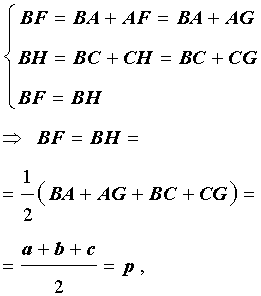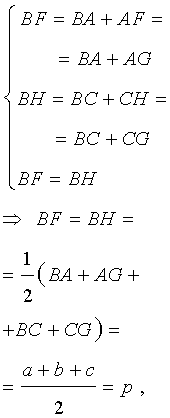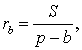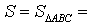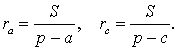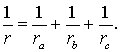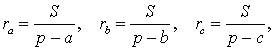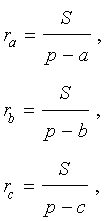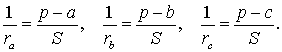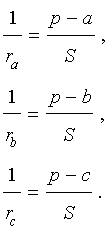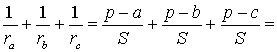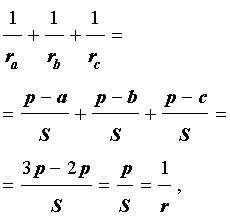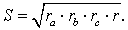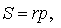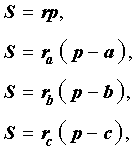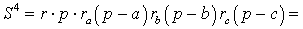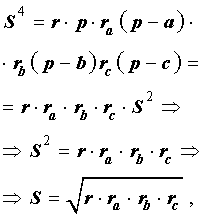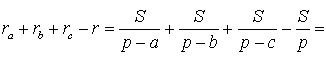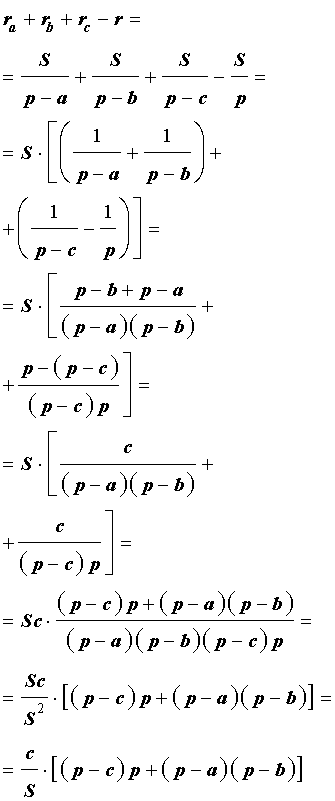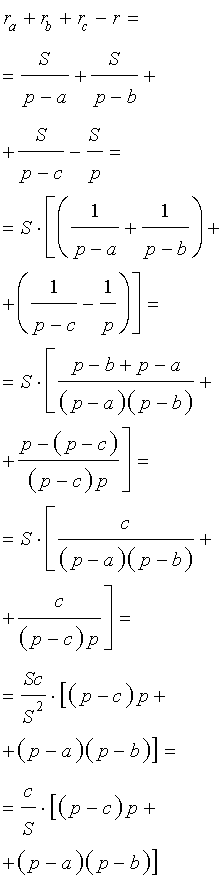Радиус вневписанной окружности равен полупериметру

Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

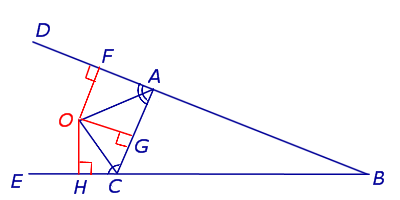
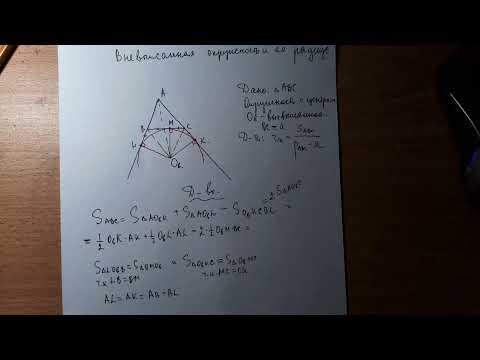
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

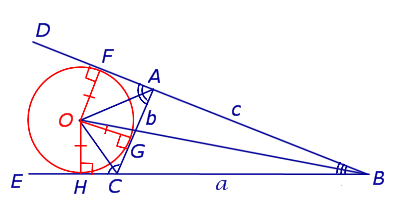
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом r_b .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

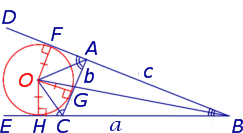
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

Следовательно, справедливо равенство

что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

,

что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

Доказательство . Перемножим формулы

что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

Преобразуем выражение, стоящее в квадратной скобке:

Видео:Это будет на ЕГЭ 2020 по математике. Вписанная и вневписанная окружности.Скачать

МАТЕМАТИКА

Рассмотрим произвольный треугольник АВС и проведем биссектрису . Затем продолжим эту биссектрису за точку до пересечения в точке с биссектрисой внешнего угла при вершине В (рис.1). Поскольку точка лежит на биссектрисе угла А, то она равноудалена от прямых АВ и ВС. Следовательно, она равноудалена и от прямых АС и ВС, а значит, лежит на биссектрисе внешнего угла при вершине С.

Продолжение биссектрисы треугольника, проведенной из одной из вершин, пересекается с биссектрисами внешних углов при двух других вершинах в одной точке.

Поскольку точка равноудалена от сторон внешних углов при вершинах В и С, то окружность с центром , касающаяся стороны ВС, касается также и продолжений сторон АВ и АС (рис.2).

Эта окружность называется вневписанной окружностью треугольника АВС. Ясно, что любой треугольник имеет три вневписанных окружности. (рис.3).

Положение центра вневписанной окружности можно охарактеризовать так: это точка пересечения биссектрис внешних углов при вершинах В и С. Можно охарактеризовать его и совершенно иначе, если заметить, что точки , В и С и центр О вписанной в треугольник АВС окружности лежат на одной окружности с диаметром (рис.4), – это следует из того, что углы и прямые.

Можно сказать, таким образом, что точка представляет собой точку пересечения прямой и окружности, описанной около треугольника ВОС.

Принимая во внимание замечание в конце статьи (Точка пересечения продолжения биссектрисы, проведенной из одной из вершин треугольника, с описанной окружностью равноудалена от двух других вершин и центра вписанной окружности), из этого можно сделать еще один вывод:

Точки, в которых вписанная и вневписанная окружности касаются стороны треугольника, симметричны относительно середины этой стороны.

В самом деле, пусть D – точка пересечения продолжения биссектрисы с описанной около треугольника АВС окружностью (рис.5). Тогда согласно упомянутому замечанию DB = DC = DO. Следовательно, D – центр окружности, описанной около четырехугольника . Проведем из точек O, D и перпендикуляры к стороне ВС и обозначим их основания буквами P, Q и R соответственно (рис.6). Точки P и R являются точками касания вписанной и вневписанной окружностей со стороной ВС, а точка Q – середина этой стороны. Но , значит, и PQ = QR, то есть точки P и R симметричны относительно точки Q.

Точка касания вневписанной окружности со стороной треугольника обладает еще одним замечательным свойством:

Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окружность касается противоположной стороны, делит периметр треугольника пополам.

Можно убедиться в этом самостоятельно, используя рис. 7.

При решении задач, связанных с нахождением площади треугольника, часто полезной бывает следующая формула. Пусть – радиус вневписанной окружности, касающейся стороны треугольника, равной а, р – полупериметр треугольника. Тогда

Обозначим эту формулу (1).

Действительно, если две другие стороны данного треугольника равны b и c (рис. 8), то

Замечание. Выпуклый четырехугольник может не иметь вписанной окружности, но он всегда имеет четыре вневписанные окружности.

Любопытно, что для площади S такого четырехугольника имеет место соотношение, похожее на формулу (1).

В самом деле, пусть стороны данного четырехугольника равны последовательно a, b, c и d; p – его полупериметр, и – радиусы вневписанных окружностей, касающихся сторон, равных а и с. Допустим, что две другие стороны не параллельны (случай параллельных сторон рассмотрите самостоятельно). Продолжим их до пересечения в точке М (рис.9).

Пусть и – точки, в которых продолжения одной из сторон касаются вневписанных окружностей, причем лежит на окружности, вписанной в маленький треугольник. Площадь S четырехугольника равна, очевидно, разности площадей большого и маленького треугольников. Периметр маленького треугольника равен , а периметр большого треугольника равен

Применяя к большому треугольнику формулу (1), а к меньшему – формулу , выражающую его площадь через радиус вписанной окружности и полупериметр, получаем:

Обозначим эту формулу (2)

С другой стороны, из подобия треугольников и ( и – центры вневписанных окружностей) находим . Но отрезок равен полупериметру большого треугольника, то есть .

Поэтому из полученной пропорции можно найти :

Подставляя это выражение в равенство (2) получим:

Спасибо, что поделились статьей в социальных сетях

Источник: Атанасян Л.С. Геометрия. Дополнительные главы к учебнику 8 кл.: Учебное пособие для учащихся школ и классов с углубленным изучением математики.

Видео:[12] Площадь через радиус вневписанной окружности. Теорема о трилистнике, трезубец, Теорема МансионаСкачать

Статья «Применение свойств вневписанной окружности при решении геометрических задач»
статья по математике

Необходимость изучения теории о замечательных точках треугольника, о вневписанной окружности и ее свойствах вызвана тем, что многие выпускники школ даже не приступают к задачам раздела С4. Актуальность изучения данной темы в том, что чаще всего именно геометрические задачи вызывают затруднения у абитуриентов и выпускников, участников математических олимпиад. Познакомить выпускников с понятием вневписанной окружности и ее свойствах необходимо как для расширения их кругозора, так и для умения решать задачи повышенной сложности.

Видео:Радиус вневписанной окружности. Вывод формулы.Скачать

Скачать:

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Предварительный просмотр:

Применение свойств вневписанной окружности при решении геометрических задач

Необходимость изучения теории о замечательных точках треугольника, о вневписанной окружности и ее свойствах вызвана тем, что многие выпускники школ даже не приступают к задачам раздела С4. Актуальность изучения данной темы в том, что чаще всего именно геометрические задачи вызывают затруднения у абитуриентов и выпускников, участников математических олимпиад. Познакомить выпускников с понятием вневписанной окружности и ее свойствах необходимо как для расширения их кругозора, так и для умения решать задачи повышенной сложности.

Данный материал был предложен учащимся для ознакомления и подготовки к ЕГЭ.

Определение: Окружность называется вневписанной в треугольник, если она касается одной из сторон треугольника и продолжений двух других сторон .

Теорема 1: У каждого треугольника три вневписанные окружности

1 свойство вневписанной окружности:

Центр вневписанной окружности лежит на пересечении биссектрисы внутреннего угла треугольника ( ∠ A) и биссектрис двух внешних углов ( ∠ B и ∠ C).

2 свойство вневписанной окружности:

Точки, в которых вписанная и вневписанная окружности касаются стороны треугольника, симметричны относительно середины этой стороны.

3 свойство вневписанной окружности:

Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окружность касается противоположной стороны, делит периметр треугольника пополам. Длина отрезка касательной, проведённой к вневписанной окружности из противоположной вершины, равна полупериметру треугольника.

4 свойство вневписанной окружности:

Площадь треугольника равна произведению радиуса вневписанной окружности на разность периметра и длины стороны треугольника касающейся вневписанной окружности

5 свойство вневписанной окружности:

где r, r a , r b , r c – соответственно радиусы вписанной и вневписанных окружностей

6 свойство вневписанной окружности:

7 свойство вневписанной окружности:

8 свойство вневписанной окружности :

9 свойство вневписанной окружности

Определение: Ортотреугольник это треугольник

∆abc вершины которого являются основаниями высот треугольника АВС.

Для ортотреугольника ( треугольника ∆abc) сам треугольник АВС является треугольником трех внешних биссектрис. Отрезки АВ, ВС и СА являются тремя внешними биссектрисами треугольника ∆abc.

Исходный треугольник АВС является ортотреугольником треугольника OaObOc.

Применение свойств к решению задач части С4 из банка ЕГЭ

Задача 1.
(сборник «Подготовка к ЕГЭ-2010, под редакцией Ф.Ф.Лысенко)

«Найдите произведение радиусов всех вневписанных окружностей треугольника со сторонами 4,5,6».

Решение: Согласно свойству 6, произведение радиусов можно найти по формуле

r a r b r c = rp 2 , где r-радиус вписанной в треугольник окружности, а р – полупериметр треугольника. Р = 4+5+6=15, р = 15/2.

r = S/p. Площадь найдем по формуле Герона: S =

Тогда r a r b r c =

Ответ:

Задача 2
(сборник «Подготовка к ЕГЭ-2010, под редакцией Ф.Ф.Лысенко)

«Найдите произведение сторон треугольника, если известно, что радиусы его вневписанных окружностей равны 9,18 и 21».

Решение: Для решения задачи воспользуемся формулой площади треугольника через радиус описанной окружности.

S= , тогда abc=S·4R. 4R=r a +r b +r c -r; S = r a r b r c /p;

р 2 = r a r b +r a r c +r b r c ; p²=9·18+9·21+18·21=27²; S=9·18·21/27=126;

4R = r a + r b + r c — r; r = r a ·r b ·r c /p²; r = 9·18·21/27² = 14/3;

4R = 9+18+21- 14/3 = 130/3; abc = 126·130/7=5460

Задачи повышенной сложности

Вневписанной окружностью треугольника называется окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон. Радиусы двух вневписанных окружностей прямоугольного треугольника равны 7 и 17. Найдите расстояние между их центрами.

Решение.

Рассмотрим прямоугольный треугольник ABC с катетами AC = b , BC = a и гипотенузой AB = c.

Пусть окружность с центром O c радиуса r c касается гипотенузы в точке T, продолжений катетов BC и AC

− в точках M и N соответственно, а p — полупериметр треугольника ABC.

Из равенства отрезков касательных, проведенных к окружности из одной точки, следует, что CM = CB + BM = CB + BT и CN = CA + AN = CA + AT , поэтому

а так как CM = CN , то CM = p. Далее, пусть окружность с центром O a радиуса r a касается катета BC в точке K , а продолжений сторон AB и AC — в точка P и Q соответственно. Рассуждая аналогично, получаем AQ = AP = p .

Четырехугольники NO c MC и KO a QC — квадраты, поэтому значит , r a r c .

Следовательно, радиус вневписанной окружности, касающейся гипотенузы данного прямоугольного треугольника, не может быть равен 7.

Таким образом, возможны только такие случаи:

1. Либо радиус окружности, касающейся гипотенузы, равен 17 , а радиус окружности, касающейся одного из катетов, равен 7;
2. либо радиусы окружностей, касающихся катетов, равны 7 и 17 .

Предположим, что r c = 17 и r a = 7 (рис. 1).

Опустим перпендикуляр O a F из центра меньшей окружности на O c N . Тогда

Следовательно,

Пусть теперь r b = 17 и r a = 7. (рис 2)

Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому точки O a , C и O b лежат на оной прямой.

Ответ: 26 или

Задание 16 № 519666

Вневписанная окружность равнобедренного треугольника касается его боковой стороны.

а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на его основание.

б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Решение.

а) Пусть b — боковая сторона треугольника, c — его основание, h — высота, опущенная на основание треугольника.

Радиус вневписанной окружности вычисляется по формуле где p — полупериметр треугольника, a — сторона, которой касается окружность.

Таким образом,

б) Пусть O 2 — центр вписанной окружности. Проведем радиус в точку касания H . Трегольники AMC и CHO 2 подобны по двум углам, поэтому

Так как R=h, то r= . Тогда CO 2 =3r. Найдем CH по теореме Пифагора. Получим, что СH=

Тогда

Откуда получаем

О твет: а) R=h ч.т.д

б) точка касания вписанной окружности с боковой стороной треугольника делит эту сторону в отношении 2:1

Таким образом: рассмотренные свойства позволили установить связь между радиусами вписанной и вневписанной окружностями, между радиусами вневписанной окружностью и площадью треугольника, между радиусами вневписанных окружностей и периметром треугольника. Данный материал выходит за рамки школьной программы и будет полезен учащимся для успешной сдачи итоговой аттестации.

Список используемой литературы:

1. Березин В.И. Сборник задач для факультативных и внеклассных занятий по математике – Москва: Просвещение, 1985 год.

2. Гнеденко Б.Г. Энциклопедический словарь юного математика. –Москва: Просвещение, 1985 год

5. Мальцев Д.А. « Математика. Все для ЕГЭ-2011» НИИ школьных технологий , 2010г.

6. Понарин Я.П. Элементарная геометрия / Я.П. Понарин. – Москва: МЦНМО, 2004 год.

7. Шарыгин И.Ф. « Геометрия 7-9» . учебник для общеобразовательных учреждений, — Москва. Дрофа. 2010г. (п. 8.1)

🎥 Видео

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вневписанная окружностьСкачать

Как найти радиус - вневписанная окружность | Олимпиадная математикаСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Как запомнить формулы Геометрии Вневписанная окружность Формула радиуса через вписанную полупериметрСкачать

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Лекция 59. Вневписанная окружность.Скачать

Окружность, радиус которой равен 14, касается одной из сторон треугольника и продолжений двух другихСкачать

Вневписанная окружность | Теоремы об окружностях - 3Скачать

Радиус описанной окружностиСкачать

4.3. Вписанные и описанные окружности. Вневписанные окружности.Скачать