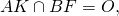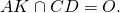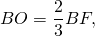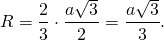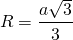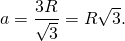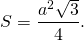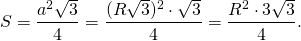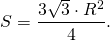Высота правильного треугольника равна 126. Найдите радиус окружности, описанной около этого треугольника.
Это задание ещё не решено, приводим решение прототипа.
Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника.
Треугольник ABC правильный, значит, все углы равны по По теореме синусов имеем:
Приведём другое решение.
В правильном треугольнике радиус описанной окружности равен двум третьим высоты. Поэтому он равен 2.
Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Окружность, описанная около правильного треугольника
Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.
1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.
Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.
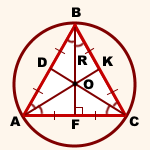
точка O — центр описанной окружности.
AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.
2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:
Таким образом, формула радиуса описанной около правильного треугольника окружности —
И обратно, сторона равностороннего треугольника через радиус описанной окружности —
3) Формула для нахождения площади правильного треугольника по его стороне —
Отсюда можем найти площадь через радиус описанной окружности:
Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —
4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.
5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности:
Видео:Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать
Свойства высоты равностороннего треугольника
В данной публикации мы рассмотрим основные свойства высоты в равностороннем (правильном) треугольнике. Также разберем пример решения задачи по этой теме.
Примечание: треугольник называется равносторонним, если все его стороны равны.
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Свойства высоты в равностороннем треугольнике
Свойство 1
Любая высота в равностороннем треугольнике одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.
- BD – высота, опущенная на сторону AC;
- BD – медиана, которая делит сторону AC пополам, т.е. AD = DC;
- BD – биссектриса угла ABC, т.е. ∠ABD = ∠CBD;
- BD – серединный перпендикуляр, проведенный к AC.
Свойство 2
Все три высоты в равностороннем треугольнике имеют одинаковую длину.
Свойство 3
Высоты в равностороннем треугольнике в ортоцентре (точке пересечения) делятся в отношении 2:1, считая от вершины, из которой они проведены.
Свойство 4
Ортоцентр равностороннего треугольника является центром вписанной и описанной окружностей.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r (следует из Свойства 3).
Свойство 5
Высота в равностороннем треугольнике делит его на два равных по площади (равновеликих) прямоугольных треугольника.
Три высоты в равностороннем треугольнике делят его на 6 равных по площади прямоугольных треугольников.
Свойство 6
Зная длину стороны равностороннего треугольника его высоту можно вычислить по формуле:
a – сторона треугольника.
Видео:Равнобедренный треугольникСкачать

Пример задачи
Радиус окружности, описанной вокруг равностороннего треугольника, равняется 7 см. Найдите сторону этого треугольника.
Решение
Как мы знаем из Свойств 3 и 4, радиус описанной окружности составляет 2/3 от высоты равностороннего треугольника (h). Следовательно, h = 7 ∶ 2 ⋅ 3 = 10,5 см.
Теперь остается вычислить длину стороны треугольника (выражение выведено из формулы в Свойстве 6):
💡 Видео
Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

2050 высота правильного треугольника равна 90 найдите радиус окружностиСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Формулы равностороннего треугольника #shortsСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

2053 радиус окружности описанной около правильного треугольника равен 56Скачать

Радиус описанной окружностиСкачать

ОГЭ 2020 задание 17Скачать

Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать