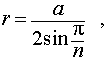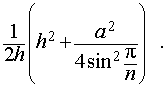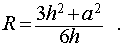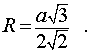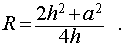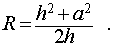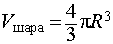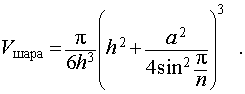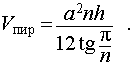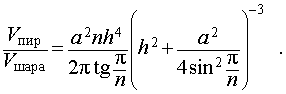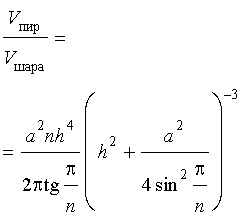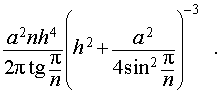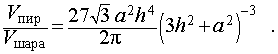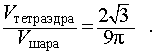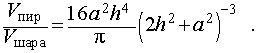Радиус окружности описанной вокруг основания правильной треугольной пирамиды

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Видео:Вычисление радиуса сферы, описанной около правильной треугольной пирамидыСкачать

Радиус окружности, описанной около основания правильной треугольной пирамиды равен 3?

Геометрия | 10 — 11 классы

Радиус окружности, описанной около основания правильной треугольной пирамиды равен 3.

Боковое ребро равно 5.

Найдите высоту пирамиды.

Полиночка, все на чертеже.

Так строится правильная треуголоная пирамида и только так!

AO это радиус описанной окружности.

SO находим по т.

Пифагора SO ^ 2 = 5 ^ 2 = 3 ^ 2 = 16, SO = 4.

Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

В правильной треугольной пирамиде радиус окружности, вписанной в основание, равен 3, высота пирамиды равна 4?

В правильной треугольной пирамиде радиус окружности, вписанной в основание, равен 3, высота пирамиды равна 4.

Найдите объём описанного шара.

Видео:Радиус описанной окружностиСкачать

Высота правильной треугольной пирамиды равна 8 см?

Высота правильной треугольной пирамиды равна 8 см.

Радиус окружности, описанной около ее основания — (8 корней из 3) см.

Вычислите : а) Длину бокового ребра пирамиды.

Б)площадь боковой поверхности пирамиды.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Высота правильной треугольной пирамиды равна 6 см?

Высота правильной треугольной пирамиды равна 6 см.

Радиус окружности, описанной около её основания — 4√ 3 (4 корней из 3) Вычислить : а) длину бокового ребра пирамиды б) площадь боковой поверхности пирамиды.

Видео:Вычисление радиуса сферы, вписанной в правильную треугольную пирамидуСкачать

Боковое ребро правильной шестиугольной пирамиды равно 6 и наклонено к плоскости основания под углом 60?

Боковое ребро правильной шестиугольной пирамиды равно 6 и наклонено к плоскости основания под углом 60.

Найдите радиус окружности, описанной около основания пирамиды.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Найдите радиус окружности, описанной около основания правильной четырехугольной пирамиды SABCD?

Найдите радиус окружности, описанной около основания правильной четырехугольной пирамиды SABCD.

Боковое ребро пирамиды равно b и образует с основанием угол aльфа.

Видео:Найти объем правильной треугольной пирамидыСкачать

Боковые ребра правильной треугольной пирамиды составляют с основанием угол в 60 градусов?

Боковые ребра правильной треугольной пирамиды составляют с основанием угол в 60 градусов.

Найдите объем описанного около пирамиды конуса, если сторона основания пирамиды равна а.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

В правильной треугольной пирамиде боковое ребро равно √37 см?

В правильной треугольной пирамиде боковое ребро равно √37 см.

Найдите объем пирамиды, если радиус окружности, описанной около основания, равен 2√3см.

Видео:№254. В правильной Треугольной пирамиде сторона основания равна а, высота равна Н. НайдитеСкачать

Боковое ребро правильной треугольной пирамиды равно 5 см Найдите площадь боковой поверхности этой пирамиды если радиус описанной около основания равен 2 корень из 3 Помогите?

Боковое ребро правильной треугольной пирамиды равно 5 см Найдите площадь боковой поверхности этой пирамиды если радиус описанной около основания равен 2 корень из 3 Помогите!

Видео:Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать

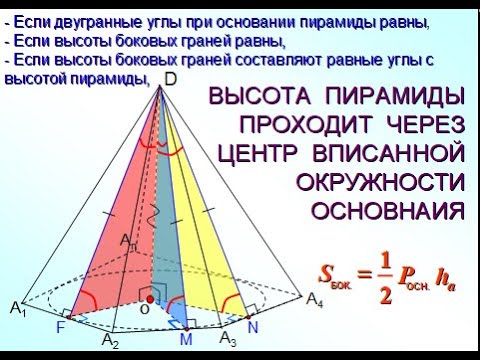
Высота правильной треугольной пирамиды равна а(корень из 3), радиус окружности, описанной около ее основания, 2а?

Высота правильной треугольной пирамиды равна а(корень из 3), радиус окружности, описанной около ее основания, 2а.

Найдите : а) апофему пирамиды б)угол между боковой гранью и основанием в)площадь боковой повверхности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Высота правильной треугольной пирамиды равна 20 см?

Высота правильной треугольной пирамиды равна 20 см.

Боковое ребро наклонено к плоскости основания под углом 60°.

А) бокового ребра ;

Б) окружности, описанной около основания пирамиды.

На этой странице находится вопрос Радиус окружности, описанной около основания правильной треугольной пирамиды равен 3?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Видео:🔴 Сторона основания правильной треугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Пирамида, вписанная в сферу

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной пирамиды

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Видео:11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

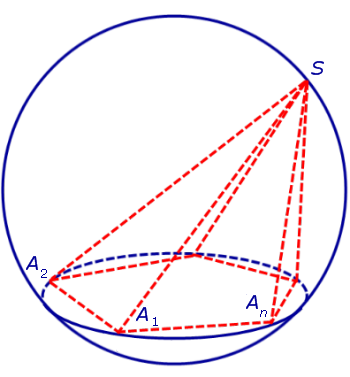
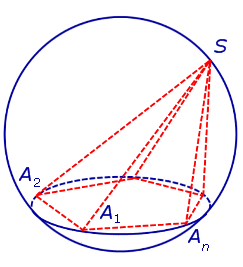
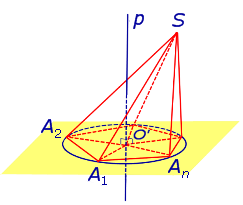
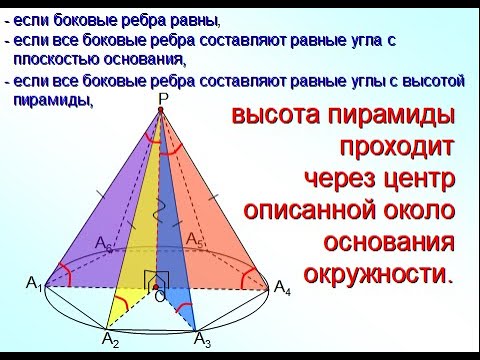
Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

На рисунке 2 изображена пирамида SA₁A₂ . A_n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A₁A₂ . A_n – основание пирамиды. Доказано.

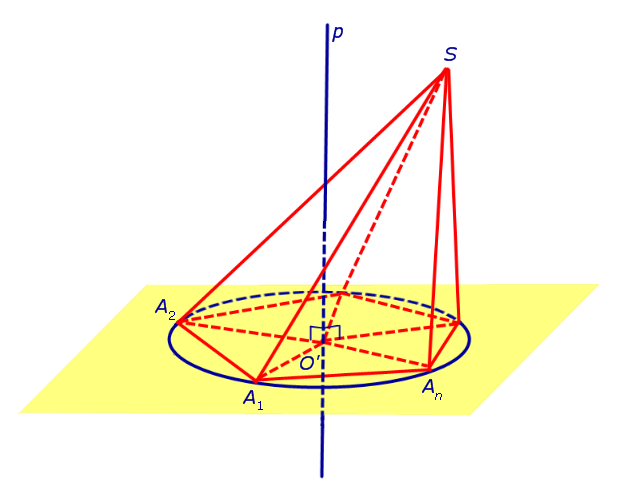
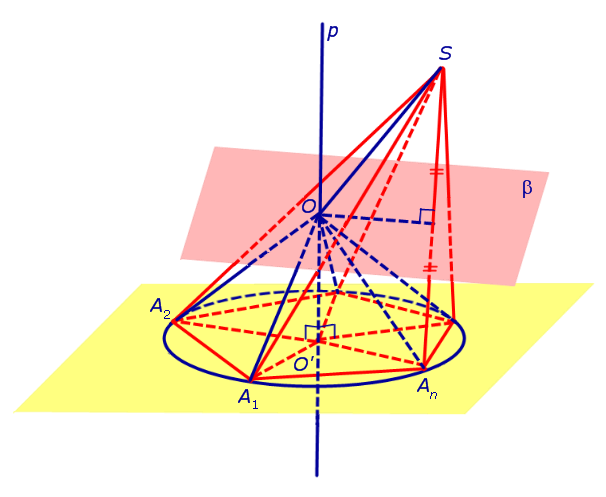
Теперь предположим, что около основания A₁A₂ . A_n пирамиды SA₁A₂ . A_n можно описать окружность. Докажем, что в этом случае около пирамиды SA₁A₂ . A_n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A₁A₂ . A_n , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A₁A₂ . A_n (рис. 3).

Рассмотрим плоскость β, проходящую через середину отрезка SA_n и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA₁A₂ . A_n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA₁A₂ . A_n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA₁A₂ . A_n .

Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A₁A₂ . A_n , что противоречит определению пирамиды.

Следствие 1. Около любой правильной пирамиды можно описать сферу.

Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Радиус сферы, описанной около правильной n — угольной пирамиды

Задача 1. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.

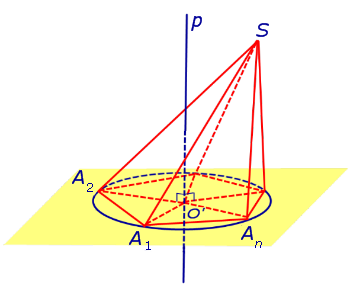
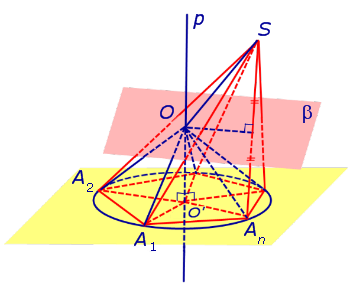
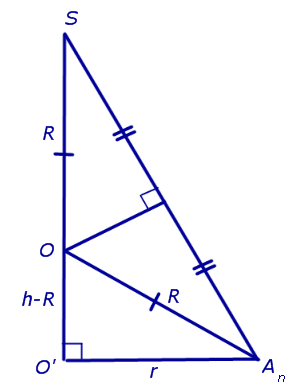
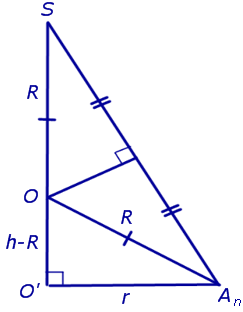
Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’A_n (рис. 5).

Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OA_n получаем

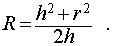(1)

из формулы (1) получаем соотношение

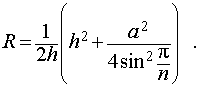(2)

Ответ.

Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен

Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен

Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен

Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Задача 2. Около правильной n — угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:

Ответ.

Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно

Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно

Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

🎥 Видео

Быстро находим радиус описанной сферыСкачать

Нахождение радиуса сферы, описанной около пирамидыСкачать

№257. Высота правильной треугольной пирамиды равна h, а двугранный угол при стороне основанияСкачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать