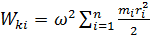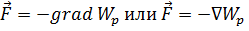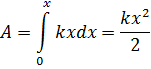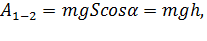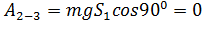Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы рассмотрим различное движение тела под действием силы тяжести и научимся находить работу этой силы. Также введём понятие потенциальной энергии тела, узнаем, как связана эта энергия с работой силы тяжести, выведем формулу, по которой находится эта энергия. С помощью данной формулы решим задачу, взятую из сборника для подготовки к единому государственному экзамену.
Видео:Физика - движение по окружностиСкачать
Работа силы тяжести.
Рассмотрим тело, скользящее по наклонной плоскости с углом наклона α и высотой Н. Выразим Δх через H и α:
.
Учитывая, что сила тяжести Fт = mg составляет угол (90° — α) с направлением перемещения, используя формулу , получим выражение для работы силы тяжести Ag:
.
Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.
Отсюда следует, что:
1. работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
2. при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).
Работа сил реакции, как следует из рисунка, равна нулю, поскольку сила реакции (N) направлена перпендикулярно перемещению Δх.
Видео:Урок 116. Работа силы тяжести. Потенциальная энергия тела, поднятого над ЗемлейСкачать
II. Работа силы при вращательном движении
Элементарная работа силы, действующей на i-тую материальную точку тела, вращающегося относительно неподвижной оси, может быть представлена в виде:
Учтем, что за малый промежуток времени dt путь, пройденный материальной точкой dl, представляет собой длину дуги окружности, по которой движется точка: dl = R·dφ.
Следовательно, dA = F·cosα·dl = F·cosα·R·dφ
С другой стороны, из определения момента силы при движении тела вокруг закрепленной оси: M = R·F.
Таким образом, с учетом скалярного произведения векторов получим:
dA = M·cosα·dφ = (M·dφ)
Полная работа при вращательном движении равна:
A = ∫dA = ∫M·cosα·dφ = ∫(M·dφ)
III. Энергия механического движения.
К механической энергии относят два вида энергии – кинетическую (Wk) и потенциальную (Wp). Чтобы получить выражение энергии в виде функции параметров состояния механического движения, надо найти, как изменяется величина энергии с изменением величины параметров.
Кинетической энергией называется энергия движущегося тела.
Для вычисления кинетической энергии подсчитаем работу, которую должна произвести результирующая сила F, чтобы тело массы m изменило скорость своего движения от V1 до V2 .
(4)
– кинетическая энергия тела. Из этой формулы следует, что кинетическая энергия тела не может быть отрицательной. Так как скорость относительная величина, то и кинетическая энергия тоже является относительной величиной.
Любую механическую систему можно представить как систему материальных точек, то кинетическая энергия механической системы может быть найдена как сумма кинетических энергий всех материальных точек, образующих эту систему: 
. Таким образом, кинетическая энергия механической системы является функцией состояния ее движения.
Работа равнодействующей силы равна изменению кинетической энергии тела, при изменении скорости его движения от V1 до V2: А = DЕК
Если действует ещё сила трения, то Aтр 2
равна: 
Просуммировав по всем элементам, получим: 
– момент инерции тела, относительно оси вращения.
(11)
Если твердое тело одновременно участвует в двух движениях: поступательном со скоростью 
и вращательном со скоростью 
, то
(12)
Полная кинетическая энергия твердого тела равна сумме кинетической энергии Wп поступательного движения центра масс тела и кинетической энергии вращения Wв.
Если на систему материальных точек или тел действуют консервативные силы, то можно ввести понятие потенциальной энергии этой системы.
Потенциальная энергия — энергия, обусловленная взаимным расположением тел или частей одного и того же тела и характером их взаимодействия.
Потенциальная энергия системы тел (или тела) может быть определена, если указаны взаимное расположение тел в системе и силы, действующие между ними.
рис. 1.9
В процессе перемещения материальной точки на dr внешняя сила F совершит работу dA = F·dr. При этом перемещении скорость тела не изменилась (была V = 0 и стала V = 0), значит в результате совершённой работы, произошло изменение другой (не кинетической) формы энергии, зависящей от координат положения тела, т.е. нужно говорить о потенциальной энергии.
Обозначим через dWp – изменение потенциальной энергии при перемещении точки в силовом поле. Согласно определению работы, можно записать:
(5)
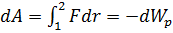
Работа, совершаемая силами F, действующими на материальную точку при её перемещении, равна изменению её потенциальной энергии.
Равенство (5) надо понимать алгебраически:
а) если dA > 0, то потенциальная энергия уменьшается (dWp 0).
Учитывая, что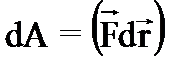 
, имеем:
(6)
Это соотношение между силой и потенциальной энергией является одним из основных соотношений механики.
Выражение 
называется градиентом изменения потенциальной энергии на пути S.
Где 
— оператор Набла, который приобретает смысл в сочетании со скалярной или векторной величиной, на которую он символически умножается. Если оператор Набла символически умножить на скаляр, то получим вектор, который называется градиентом функции.
Из этого выражения (6) следует:
а) Сила направлена всегдав сторону уменьшения потенциальной энергии.
б) производная обращается в ноль в точках, где функция достигает максимума или минимума, а это значит – где потенциальная энергия имеет максимум или минимум, там сила равна нулю.
Уравнение (5) не даёт полного определения величины потенциальной энергии в каждой точке, а определяет лишь изменение потенциальной энергии при переходе от точки к точке. Абсолютная величина Wp зависит от выбора начала отсчёта потенциальной энергии (где потенциальная энергия равна нулю). Обычно, за начало отсчёта выбирают такое положение, при котором взаимодействие практически отсутствует (когда тела удалены в бесконечность).
Вычислим величину потенциальной энергии в двух случаях:
1. Потенциальная энергия тяготения.
Откуда получим: 
В частном случае, при r1 = 0, (на поверхности Земли), r2 = H, (над поверхностью Земли)
2.Потенциальная энергия упругодеформированного тела.
| Рис. 1.10 |
Покажем, что работа силы тяжести одинакова для двух разных путей (для пути 1 — 3 и пути 1 — 2 — 3), обозначения длин путей приведены на рис. 1.10.
Из последней формулы следует, что работа силы тяжести не зависит от формы траектории. А вдоль замкнутой траектории равна нулю, что подтверждает вывод о консервативной природе силы тяжести.
Полной механической энергией системы называют величину, равную сумме кинетической и потенциальной энергии этой системы:
Полная механическая энергия также является функцией состояния, как и каждое из слагаемых.
📽️ Видео
Подготовка к лабораторной работе "Движение тела по окружности под действием сил тяжести и упругости"Скачать
Лабораторный эксперимент №4 - Изучение движения тела по окружности (9 класс)Скачать
Урок 90. Движение по окружности (ч.2)Скачать
Движение тел по окружностиСкачать
Движение тела под действием силы тяжести. 1 часть. 9 класс.Скачать
Физика | Равномерное движение по окружностиСкачать
Работа силы тяжести. Работа силы упругости. Потенциальная энергия | Физика 10 класс #20 | ИнфоурокСкачать
Движение по окружностиСкачать
Урок 89. Движение по окружности (ч.1)Скачать
Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать
Урок 120. Работа силы упругости.Скачать
Урок 87. Движение по наклонной плоскости (ч.1)Скачать
Урок 81. Устойчивость тел в присутствии силы тяжестиСкачать
Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать
Движение по окружности (учебный фильм)Скачать
Виртуальная лабораторная работа - Движение тела по окружности под действием сил тяжести и упругостиСкачать
Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать
Урок 62. Сила тяжести и вес тела. Невесомость.Скачать
