Программирование движения по окружности (8 видео)

Программирование движения рабочего органа по дуге окружности (круговая интерполяция)

При обработке фасонного участка детали (тела вращения), являющегося отрезком радиусной дуги, программа перемещения центра инструмента по дуге задаётся в пределах одного квадранта. Признаком круговой интерполяции является функция G02 (G20, G21) или G03 (G30, G31) — табл. 3.8.

После функции G02 (G20, G21) или G03 (G30, G31) в программе задаются координаты точки начала дуги относительно центра дуги (точки 0) по адресам: I по оси X, К — по оси Z (всегда со знаком «+») и величины приращений ЛА и AZ по осям Xи Zсо своими знаками (рис. 3.4, а и б).

Структура кадра: N003G02 +1 + К АХ AZ F LF

В тех случаях, когда отрезок дуговой траектории расположен в секторе с углом не менее 90°, в геометрической информации будут значения координат I и К и приращения по осям Хи Z (рис. 3.4, а и б).

Если точка начала дуги лежит на одной из осей, т.е. одна из координат этой точки будет совпадать с координатой центра дуги, то признак второй координаты в кадре может отсутствовать: точка на оси X- может отсутствовать адрес К; точка на оси Z- может отсутствовать адрес I (рис. 3.4, в и г).

Содержание

Управление движением робота
Варианты передвижения робота на колесах
Робот за 3 минуты
Расчет числа оборотов
Разворот на месте
Поворот вокруг одного колеса
Движение по окружности произвольного диаметра
Движение по линии с объездом препятствия (кирпич)
Вращение 2D объекта по окружности
🎬 Видео

Видео:АЛГОРИТМ ДВИЖЕНИЯ ПО ОКРУЖНОСТИСкачать

Управление движением робота

Видео:Физика | Равномерное движение по окружностиСкачать

Варианты передвижения робота на колесах

В общем случае робот может передвигаться прямолинейно и по ломанной траектории. Вычислить передвижение робота на необходимое расстояние по прямой достаточно просто. Для этого должен быть известен диаметр колеса робота. Исходя из этих начальных условий можно вычислить точное количество оборотов колеса, необходимое для преодоления заданного расстояния.

Видео:Физика - движение по окружностиСкачать

Робот за 3 минуты

Зная количество оборотов мотора робота в минуту можно вычислить время, за которое робот преодолеет нужное расстояние.

Для робота Lego EV3 количество оборотов большого мотора составляет 160 – 170 оборотов в минуту.

Поэтому вычисление времени будет приблизительным т.к. у каждого мотора количество оборотов в минуту может быть разным.

Ломанная траектория представляет из себя комбинацию из прямолинейных и криволинейных участков. Криволинейные участки можно вычислять, используя формулу вычисления длины окружности.

Видео:ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Расчет числа оборотов

Для того, чтобы рассчитать количество оборотов колеса для движения на заданное расстояние по прямой нужно использовать длину окружности колеса. Она вычисляется по формуле L = π * d. Где π – число Пи, равное 3,14, а d –диаметр колеса. Для базового набора Lego EV3 диаметр колеса составляет 56 мм.

Пусть робот EV3 оснащен двумя передними колесами и шаровой опорой сзади и должен проехать 1 метр. За один оборот колеса робот преодолевает расстояние L = π * d = 3.14 * 56 = 175,84 мм. Пусть n – количество оборотов, k – заданное расстояние. Тогда количество оборотов n = k / L =>

n = 1000 мм / 175,84 мм = 5,69 оборотов.

Программа для Lego EV3 для движения робота на заданное количество оборотов.

Во вкладке «Движение» выбираю блок «Рулевое управление».

Устанавливаю режим «Включить на количество оборотов», «Рулевое управление» установлено в 0 – это означает движение по прямой линии. Большие моторы установлены в порты B и C.

Скорость движения моторов – 50 условных единиц. Значение оборотов ставлю вычисленное выше. Тормозить в конце – значение «Истина». При нажатии на блок «Начало» робот Lego EV3 проедет по прямой 1 метр со скоростью 50 у.е. и остановиться.

При втором способе используется блок «Независимое управление моторами».

независимое управление движение вперед на один метр

Все настройки блока такие же, как и настройки у блока «Рулевое управление». Для того чтобы робот ехал по прямой необходимо скорость моторов установить одинаковой.

В общем случае робот может передвигаться по траектории, которая представляет из себя окружность, часть окружности и комбинации различных частей окружности. При этом робот может:

Разворачиваться на месте – колеса робота крутятся в разные стороны с одинаковой скоростью;
Разворачиваться вокруг одного колеса – одно колесо машинки Lego EV3 стоит на месте, другое крутится с заданной скоростью;
Описывать произвольную окружность – оба колеса крутятся в одном направлении с разной скоростью.

Пусть параметры тележки EV3 будут такими: робот представляет из себя платформу с двумя колесами и шаровой опорой, расположенной сзади. Тележка симметрична и расстояние между центральными осями колес и шаровой опорой является равнобедренным треугольником.

робот тележка лего

Для упрощения расчетов, задам расстояние между центрами колес по оси, но которой они расположены равным 20 см. На многих соревнованиях по робототехнике одним из условий являются габариты робота. Например, нужно чтобы размеры робота были не более 20 см в ширину, 20 см в длину и 20 см в высоту.

Если робот не подходит по габаритам, то его не допускают к соревнованиям. Диаметр колеса 0,56 см – это стандартный размер колеса из базового набора Lego EV3. Левый большой мотор подключен к порту В, правый к порту С. Теперь вычислим количество оборотов колеса для каждого случая и для разворота робота Lego EV3 на определенный угол.

Расчеты применимы для роботов, собранных на базе любых конструкторов. Разница будет заключаться только в среде программирования, т.к. у разных робототехнических наборов разные программные обеспечения. Но принцип расчета везде одинаковый.

Видео:Математика это не ИсламСкачать

Разворот на месте

Разворот робота на 360 градусов

В этом случае нужно чтобы у робота колеса вращались в разных направлениях с одинаковой скоростью. Для того чтобы робот совершил полный разворот вычислим необходимую длину окружности. Разворот будет на месте, поэтому диаметр между осями будет равен 20 см =>

Длина описываемой окружности будет равна
L = π * d = 3.14 * 0,2 м = 0,628 метра

Количество оборотов будет равно пройденному расстоянию L деленному на длину окружности колеса n = Lокр / L колеса, где длина окружности колеса равна L = π * d = 3.14 * 56 = 175,84 мм = 0,176 м.

А значит количество оборотов для разворота на 360° будет равно

n = L окр / L колеса = 0,628 / 0,176 = 3,568 оборота.

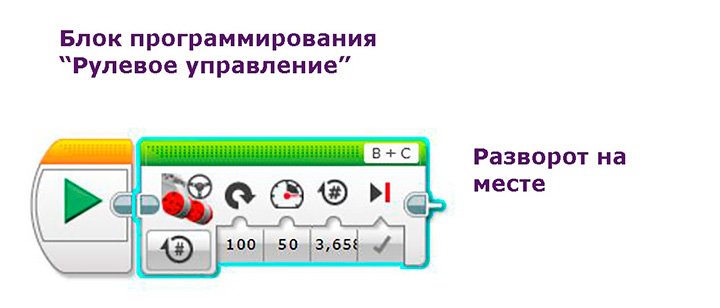
Для блока программирования «Рулевое управление» можно задать разворот на 100 условных единиц (или — 100), что означает разворот на месте. Скорость 50 у.е. и 3,568 оборота.

разворот робота на месте рулевое управление

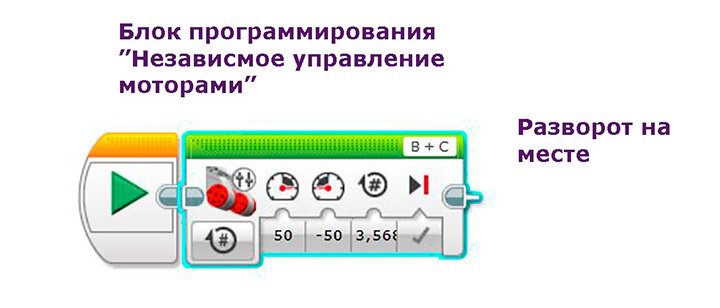
Для блока программирования «Независимое управление моторами» просто скорость одного мотора ставим 50 у.е., а другого – 50 у.е. При этом количество оборотов колес остается 3,568.

разворот робота на месте независимое управление

Для того, чтобы повернуть робота тележку Lego EV3 на произвольное количество градусов нужно составить пропорцию, где нужное количество градусов нужно разделить на 360 градусов и учесть эту пропорцию в расчете.

Например, для разворота на 180 градусов. Обозначим нужную длину части окружности L1 =>

L1 = L * (нужное к-во градусов / 360 градусов) = L * (180 / 360) = L / 2 = 0,628 / 2 = 0,314, а значит к-во оборотов

n = L1 / L колеса = 0,314 / 0,176 = 1,784 оборота.

Видео:JavaScript. Движение точки по окружности с использованием формул.Скачать

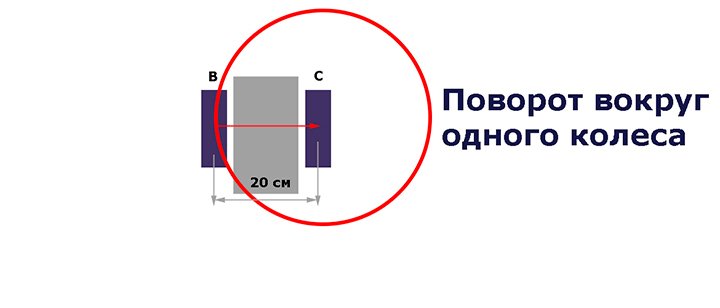
Поворот вокруг одного колеса

В этом случае у нас радиус поворота будет 20 см, а диаметр описываемой окружности 40 см. Поэтому длина описываемой окружности будет в два раза больше и как для полной окружности, так и для ее части нужно просто предыдущие вычисления умножить на два.

Поворот робота вокруг одного колеса

Для того чтобы сделать поворот вокруг одного колеса на 360 градусов нам понадобится в предыдущей формуле d умножить на 2, а значит и количество оборотов колеса увеличится вдвое.

L = π * 2 * d = 3.14 *2 * 0,2 м = 1,256 метра

Для робота собранного на базе набора Lego EV3 целесообразно применить программирование с помощью блока «Независимое управление моторами». Где одному мотору задать нулевое значение оборотов, а другому вычисленное. При повороте на 360 градусов это будет 7,136 оборота.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

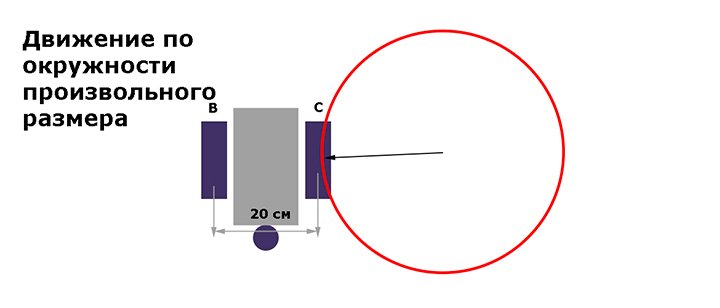
Движение по окружности произвольного диаметра

Пусть расстояние от центра окружности до середины первого колеса будет R1. Расстояние от центра окружности до середины второго колеса R2.

В этом случае мы получаем движение колес по окружностям разного диаметра за одинаковое время. Регулировать такое передвижение можно за счет разности скоростей внешнего и внутреннего колеса.

Длина окружности, которую проезжает правое колесо обозначим как L1

Движение робота по окружности произвольного размера

L1 = 2 * π * R1

Длина окружности для левого колеса

L1 = 2 * π * (R1 + R2)

Скорость правого колеса V1, а скорость правого колеса V2.
Время за которое заданное расстояние пройдет правое колесо t1.

t1 = L1 / V1 = (2 * π * R1) / V1

Время, за которое заданное расстояние пройдет левое колесо t2.

t2 = L2 / V2 = (2 * π * (R1 + R2)) / V2

Время проезда окружности или ее части левым и правым колесом у нас одинаковое t = t1 = t2, а значит и правые части выражений равны.

L1 / V1 = L2 / V2 ó (2 * π * R1) / V1 = (2 * π * (R1 + R2)) / V2 ó

Упрощаем выражение и получаем следующую пропорцию

V2 / V1 = (R1 + R2) / R1

Сейчас можно вычислить скорости левого и правого колеса для заданной окружности. Пусть у нас R1 = 20 см и R2 = 20 см, для упрощения скорость левого колеса возьмем 100 условных единиц. Тогда

V2 / V1 = (R1 + R2) / R1 ó 100 / V1 = (20 + 20) / 20

100 / V1 = 2 ó V1 = 100 / 2 ó V1 = 50 условных единиц.

Имея вычисленные значения скоростей можно составить программу прохождения участка. Для робота Lego EV3 можно использовать блок программирования «Независимое управление моторами». Скорость левого двигателя устанавливаем 100 у.е., скорость правого двигателя устанавливаем 50 у.е.

Независимое управление моторами Lego EV3 произвольная окружность

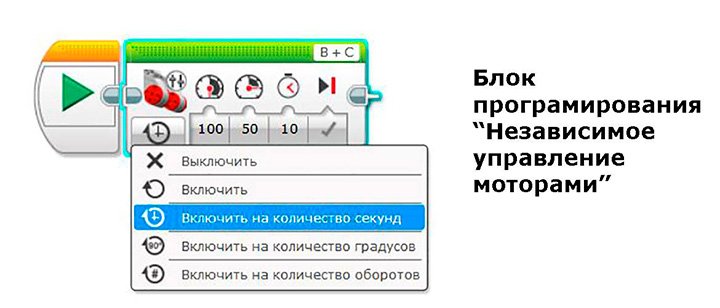
Режим устанавливаем «Включить на количество секунд». Произвольно установим 10 секунд. Для того, чтобы точно проходить заданное расстояние нужно замерить время прохождения одного круга секундомером. Зная это время можно задавать нужное нам расстояние.

Часто на соревнованиях одним из заданий является движение робота по черной линии с объездом препятствий. И для успешного преодоления трассы необходимо вычислить траекторию объезда. При помощи таких вычислений это сделать достаточно легко.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Движение по линии с объездом препятствия (кирпич)

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Вращение 2D объекта по окружности

Привет, если ты читаешь эту статью, значит ты хочешь узнать ответ на вопрос «как работает вращение объекта в 2D ?»

Ты скорее всего знаешь что во всех современных движках, таких как Unity вращение осуществляется с помощью функции, но нам интересно, как можно написать алгоритм
вращения своими руками.

Если проще то наш алгоритм работает так.

Мы представляем окружность, где:

Центр это точка, вокруг которой мы вращаем объект.
Радиус — расстояние от центра до вращаемого объекта.

Итак, начнем.

Давайте взглянем на рисунок ниже:

Дано: длинна радиуса, координаты точки вращения, угол АОВ, АВ перпендикулярен оси ОХ.
Задача: Задать вращение точки А на 360 градусов с помощью формулы.
Рассмотрим: треугольник ОАВ:
угол ОВА — прямой => треугольник ОАВ — прямоугольный треугольник;
тогда:
гипотенуза = радиусу окружности с центром в точке О
угол поворота = от 1 до 360 градусов
тогда чтобы найти катеты ОВ и АВ нужно:
АВ = радиус * cos(угла поворота),
ОВ = $inline$радиус * sin(угла поворота)$inline$
Теперь когда мы знаем размеры катетов
мы составим формулу:
для координаты по x:$inline$позиция по x = радиус * cos(угла поворота) + начальная позиция по x$inline$,
и для координаты по y: $inline$позиция по y = радиус * sin(угла поворота) + начальная позиция по y$inline$

Давайте попробуем применить формулы:

Не сложно догадаться что делает этот код, а именно вращает наш кружок по оси, но почему лишь один раз?

Давайте вспомним уроки геометрии в седьмом классе: градусная мера угла не может превышает 360 градусов.

А если попробуем обнулять угол вращения, когда тот будет больше 360 градусов, давайте посмотрим что из этого выйдет:

Этот код позволяет вращать кружок по оси бесконечно.

Однако у этой формулы есть один недостаток: можно вращать объекты только на 1 оборот. Это значит что нам нужна другая формула.

Давайте улучшим нашу формулу:

Дано:
треугольник ОАВ — прямоугольный
катет 1 = x1 — начальная координата X
катет 2 = y1 — начальная координата y

Задача:
улучшить формулу так, что-бы можно было вращать точку А на неизвестный угол.

Решение:
Из предыдущей задачи мы знаем что:
$inline$$inline$xPos = (lineLong * cos(a)) + StartPosX$inline$$inline$. => $inline$cos(a) = xPos — startPosX: (lineLong )$inline$

И теперь мы можем вывести формулу по нахождению угла a
$inline$yPos = (lineLong * sin(a)) + StartPosY$inline$ => $$display$$a = arccos((xPos — startPosX): lineLong)$$display$$.

А сейчас обновим нашу формулу и получим: $$display$$xPos = (lineLong * cos(a +b)) + startPosX$$display$$

Теперь у нас есть формула которая позволяет бесконечно вращать точку по окружности: $$display$$xPos = (lineLong * cos(a +arccos((xPos — startPosX): lineLong))) + startPosX$$display$$

Давайте напишем код, который будет вращать наш объект по нажатию на клавишу.

Примерно таком образом решается эта задача.

Надеюсь, ты смог извлечь полезную информацию из моего поста, желаю удачно применить полученные знания на практике