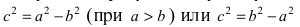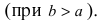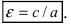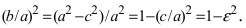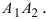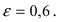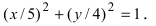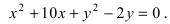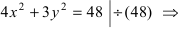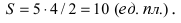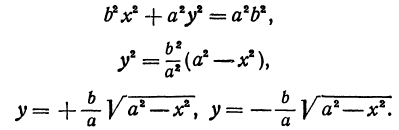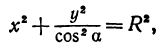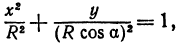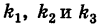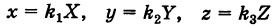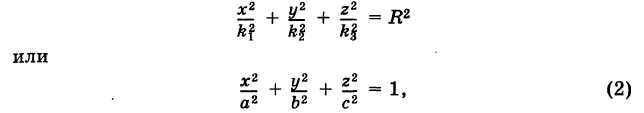При выполнении машиностроительных чертежей часто возникает необходимость построения прямоугольных проекций окружности.
Если окружность лежит в плоскости уровня, то, естественно, она проецируется на одну из плоскостей проекций в натуральную величину, а на другую плоскость проекций — в отрезок, совпадающий с вырожденной проекцией плоскости.
| Рис.8.5 |
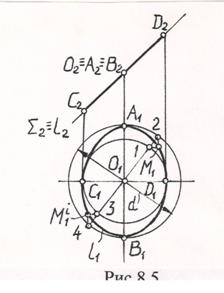
На П2 отрезок С2D2 равен d. На П1 эллипс l1 строим известным способом с помощью окружностей радиусами малой и большой полуоси эллипса, делением окружностей диаметральными линиями и получением точек М i .
Окружность, лежащая в плоскости общего положения, проецируется на обе плоскости проекций в эллипсы.
| Рис.8.6 |
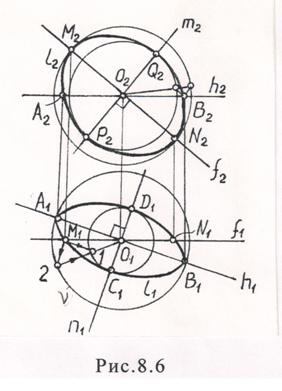
Отметим, что большие оси эллипсов l1,l2 принадлежат линиям уровня, соответственно горизонтали h и фронтали f и по величине равны диаметру окружности l. Поэтому большую ось А1В1 эллипса l1 на П1 откладываем на горизонтальной проекции горизонтали h1, а большую ось М2N2 эллипса l2 — на фронтальной проекции фронтали f2. Вторые проекции А2В2, М1,N1 находим из условий принадлежности соответственно точек А,В,М,N горизонтали и фронтали.
Для построения малых осей С1Д1 и Р2Q2 проводим прямые n1^А1В1, m2^М2N2. Эллипс l1 теперь определен большой осью А1В1, направлением n1 малой оси и двумя точками М1,N1. Этих условий достаточно для графического определения величины его малой оси:
¨ через точку М1 искомого эллипса l1 проводим прямые, параллельные А1В1 и n1;
¨ отмечаем точку 2 пересечения прямой, параллельной n1, с окружностью u, описанной на А1В1, как на диаметре;
¨ отмечаем точку 1=012ÇМ11 и получаем отрезок 011, определяющий величину малой полуоси эллипса l1.
Аналогично определяется величина малой полуоси эллипса l2 — фронтальной проекции окружности l.
Обводы
Решение ряда задач требует построения линий, проходящих через упорядоченный массив точек или через данные точки и имеющие в них наперед заданные положения касательных, кругов кривизны и т.д. Иногда требуется какую-либо графически или аналитически заданную кривую заменить другой кривой.
Если исходная кривая задана большим числом точек, то выбор новой кривой, качественно заменяющей исходную, требует выполнения сложных вычислений. Для упрощения решения задачи в качестве заменяющей линии конструируют составную кривую — обвод.
Обводом называется линия, составленная из дуг кривых выбранного вида, которые в стыковых точках имеют определенный порядок соприкосновения.
В инженерной практике в качестве составляющих обводов обычно используют отрезки прямых, дуги кривых второго и третьего порядка. Порядок составляющих в стыковых точках определяет порядок гладкости обвода. Если смежные составляющие имеют в стыковых точках общие касательные, то составная линия называется обводом первого порядка гладкости. Составная линия представляет собой обвод второго порядка гладкости, если график изменения кривизны по ее длине будет непрерывным.
Рассмотрим один из способов построения обводов — радиусографический.
| Рис.8.7 |
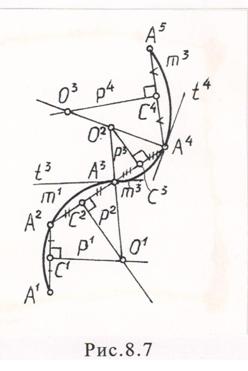
Построение составляющих обвода основано на простых свойствах окружностей при построении их сопряжений. Первая составляющая m 1 однозначно определяется первыми тремя точками А 1 ,А 2 ,А 3 . Центр О 1 дуги m 1 строится как точка пересечения перпендикуляров р 1 ,р 2 , восстановленных из середин С 1 ,С 2 ее хорд — А 1 А 2 , А 2 А 3 .
Вторая и последующие составляющие m 2 , m 3 определяются двумя точками и касательной, построенной к предыдущей составляющей в стыковой точке. Центр О 2 второй составляющей m 2 определяется как точка пересечения прямой О 1 А 3 , соединяющей центр О 1 предыдущей окружности со стыковой точкой А 3 , с перпендикуляром р 3 , восстановленным из середины С 3 хорды А 3 А 4 . Аналогично строится все последующие составляющие m j (j=1,2. n-2).
Вопросы для самопроверки к лекции 8:
1. Как принято рассматривать кривую линию в начертательной геометрии?
2. Назовите основные понятия, характеризующие кривую линию.
3. Назовите проекционные свойства кривых линий.
4. Как может проецироваться окружность на плоскости проекций?
5. Что называется обводом?
ПОВЕРХНОСТИ
Поверхности составляют обширное многообразие нелинейных фигур трехмерного пространства. Любое тело ограничивается своей поверхностью. Нет ни одной области деятельности человека, где бы он не сталкивался с поверхностями в виде материальных, физических моделей.
Инженерная деятельность связана непосредственно с конструированием, расчетом, изготовлением различных технических поверхностей. Большинство задач прикладной геометрии сводится к автоматизации конструирования, расчету и воспроизведению сложных технических поверхностей.
Основные понятия и определения
В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F(x,y,z)=0, где F(x,y,z) -многочлен n-й степени, или в форме какой либо трансцендентной функции. В первом случае поверхности называют алгебраическими, во втором — трансцендентными.
Если алгебраическая поверхность описывается уравнением n -й степени, то поверхность считается n-го порядка. Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет сама поверхность. Порядок поверхности может быть определен также числом точек ее пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
| Рис.9.1 |
В начертательной геометрии геометрические фигуры задаются графически, поэтому поверхность целесообразно рассматривать кинематически: как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии. Образование поверхности с помощью линии позволяет дать иное определение поверхности, базирующееся на основных элементарных геометрических понятиях, таких как точка и множество. Действительно, если принять, что положение движущейся в пространстве линии будет непрерывно меняться с течением времени t, и принять t за параметр, то поверхность можно рассматривать как непрерывное однопараметрическое множество линий. В свою очередь, линия определяется как непрерывное однопараметрическое множество точек, поэтому можно дать следующее определение поверхности: поверхностью называется непрерывное двухпараметрическое множество точек.
Изображение по-верхности на плоскости проекций получают обычно заданием перемещающейся l и направляющей линий m с указанием характера перемещения подвижной линии (рис. 9.1.) Перемещающаяся линия называется образующей. Характер перемещения образующей может быть определен, например, с помощью проецирующей плоскости S.
Процесс образования и изображения показанной поверхности можно записать так:
Эти условия сохраняются и на проекции поля П1.
| Рис.9.2 |
Упорядоченное множество точек или линий, принадлежащих поверхности, называется ее каркасом. В зависимости от того, чем задается каркас поверхности, точками или линиями каркасы подразделяются на точечные и линейчатые.
Линейчатый каркас считается непрерывным, если его параметр выражается непрерывной функцией, в противном случае он называется дискретным.
Поверхность будет задана (определена), если в любой момент движения образующей будут известны ее положение и форма, а это в свою очередь позволяет однозначно отвечать на вопрос положения точки на данной поверхности.
Кинематический способ образования поверхности подводит нас к понятию определителя, под которым мы будем подразумевать необходимую и достаточную совокупность геометрических элементов и связей между ними, которые однозначно определяют поверхность.
В определитель должны быть включены:
1. Геометрическая часть, определяющая перечень геометрических элементов, участвующих в образовании поверхности.
2. Алгоритмическая часть, указывающая на взаимосвязь между геометрическими элементами.
Итак, определитель поверхности состоит из двух частей: из совокупности геометрических элементов (1-я часть) и дополнительных сведений (2-ая часть).
В общем случае определитель будет иметь следующую структурную форму:
Ф (Г) [А], где (Г) — геометрическая часть,
[А] — алгоритмическая часть.
Для определения конкретного вида поверхности в каждую часть определителя вкладывается конкретное содержание.
Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Проецирование окружности
Окружность с центром О, рассматриваемая как плоская фигура, проецируется без искажения на ту плоскость, которой она параллельна (рис. 6.5). При этом две другие ее проекции есть отрезки, параллельные осям проекций и равные по длине диаметру окружности.
Если окружность наклонена к плоскости проекций, то ее проекция представляет собой эллипс, большая ось которого равна диаметру окружности. Величина малой оси зависит от угла наклона плоскости окружности к плоскости проекций.
Окружность, изображенная на рис. 6.6, перпендикулярна плоскости проекций П и наклонена к плоскости проекций к2, поэтому ее фронтальная проекция — эллипс. Большая ось этого эллипса С «И « представляет собой проекцию диаметра окружности, который без искажения проецируется на плоскость проекций л2. Таким образом, она перпендикулярна плоскости проекций Л1 и параллельна плоскостям проекций 7^2 и Лз. Малая ось эллипса является проекцией диаметра АВ, перпендикулярного СИ. Ее величину на плоскости проекций п2 определяют с помощью линий проекционной связи, проведенных через точки А’ и В’.
Промежуточные точки эллипса находят с помощью дополнительной плоскости проекций тс4, которую располагают параллельно плоскости окружности, поэтому окружность проецируется на нее без искажения. Вначале строят новую проекцию центра окружности — точку О™ и на плоскости тс4 описывают заданную окружность. Затем на окружности намечают 8 или 12 произвольных точек и находят их проекции в системах плоскостей щ/щ и щ/л2. На рис. 6.6 приведено построение только для двух промежуточных точек 1 и 2; остальные строят аналогично.
Окружность, расположенная в плоскости общего положения, проецируется на все основные плоскости проекций в виде эллипсов, большие оси которых равны ее диаметру. Величины малых осей обычно различны и зависят от углов

наклона заданной плоскости, в которой расположена окружность, к плоскостям проекций.
Если эллипс представляет собой проекцию окружности, то на горизонтальной проекции его большая ось расположена на горизонтальной прямой плоскости, на фронтальной — на фронтальной прямой и на профильной — на профильной прямой.
Построение в плоскости общего положения а(Иа п /а) (рис. 6.7) проекций окружности с центром в точке О, расположенной на горизонтальной прямой /га, и с радиусом, равным /?, начинают с определения проекций осей эллипса.
На горизонтальной проекции окружности по прямой /га‘ вправо и влево от точки О‘ откладывают радиус окружности Л, получая при этом точки А’ я В’. Сделав замену плоскостей проекций щ/л2 —> п/щ, где п4_1_ Иа, и построив новую проекцию окружности в виде отрезка С ,У /) |У , равного диаметру окружности, строят с помощью точек С’ и /)’ малую ось эллипса на горизонтальной проекции (направления построений указаны стрелками).
Для фронтальной проекции окружности через точку О « проводят проекцию прямой, параллельной^’, и на ней вправо и влево от точки О » откладывают радиус окружности Я, получая точки Е «, Е». Сделав замену плоскостей проекций П/П2 —> П2/Л5, где п5 Е/а, и построив новую проекцию окружности в виде отрезка, равного диаметру окружности, строят на фронтальной проекции с помощью точек 1У, малую ось эллипса.
Таким образом, на каждой проекции есть по четыре точки, принадлежащие проекции окружности: точки Л ‘, ВС‘, В‘ и Е «, Е», К «, Ь». Проводя из них линии проекционной связи, получают восемь точек для построения горизонтальной и фронтальной проекций эллипса.
Видео:Как начертить овал во фронтальной плоскостиСкачать

Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 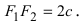
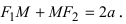
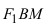
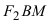
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 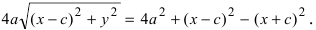
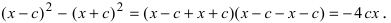
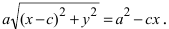
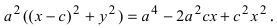
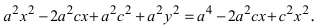
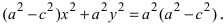
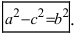
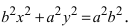
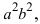
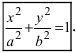
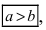
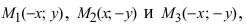
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
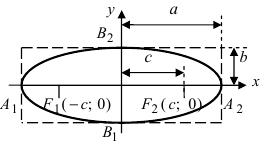
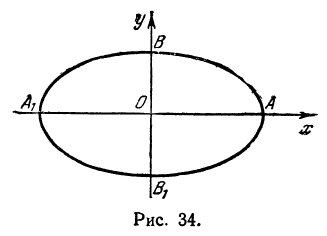
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 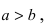
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 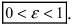
Если 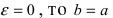
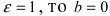
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 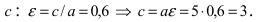
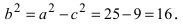
Пример:
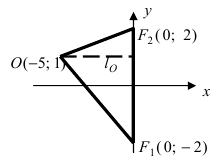
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 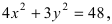
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
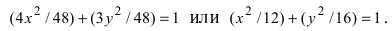
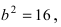
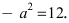
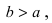
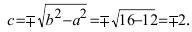
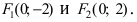
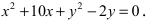
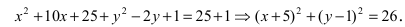
Построим в декартовой системе координат треугольник 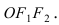
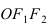
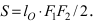
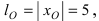
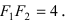
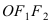
Видео:Задание 21 Проецирование окружностиСкачать

Эллипс в высшей математике
где 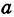
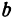
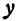
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
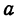

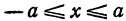
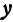
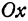
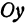
При 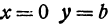
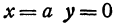
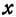

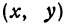
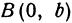
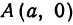
Полученная линия называется эллипсом. Число 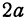
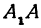
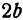
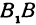
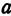
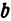
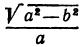
Пример:
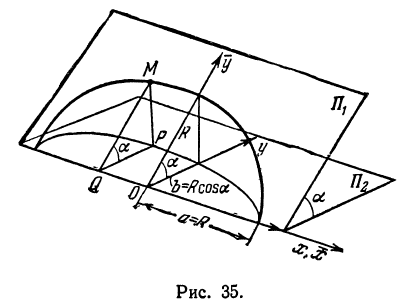
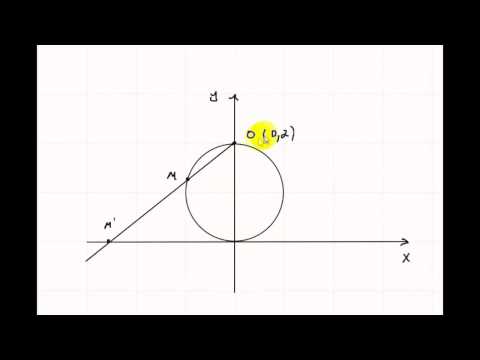
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 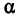
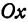
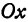
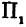
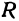
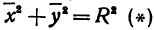
Пусть точка 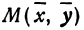
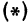
Обозначим проекцию точки 
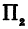
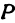
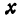
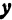


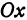
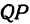
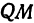
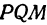
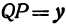
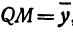
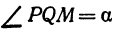
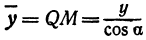


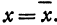
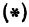
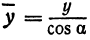
а это есть уравнение эллипса с полуосями 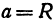
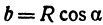
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 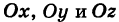
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 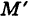
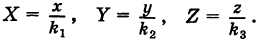
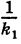
Подставляя эти формулы в уравнение (1), будем иметь
где 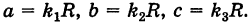
Величины 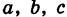
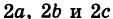
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎬 Видео
КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Проекции окружности расположенной в плоскости общего положения. Метод вращенияСкачать
Как начертить овал в горизонтальной плоскостиСкачать

ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

10 класс, 11 урок, Числовая окружностьСкачать

2 3 проекция точки на конусеСкачать

Изометрическая проекция окружности в плоскости ХУСкачать
Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Как начертить цилиндр в объемеСкачать

Построение окружности в диметрииСкачать

Как начертить овал в профильной плоскостиСкачать

Построение окружности в изометрииСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Полезные мелочи | стереографическая проекция | сфера на плоскостьСкачать

Полезные мелочи | стереографическая проекция | окружность на прямую | 1Скачать


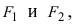
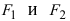
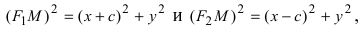
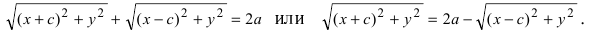
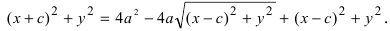
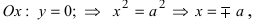 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 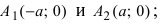
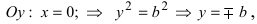 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 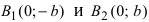 (Рис. 30).
(Рис. 30).