Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, что такое окружность и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.
Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

Что такое окружность?
Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.
Видео:Окружность и круг, 6 классСкачать

Что такое круг?
Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.
У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).
Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.
Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Примеры круга в реальной жизни
На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.
Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Видео:Окружность. 7 класс.Скачать

Отличия окружности от круга
Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.
Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — это граница круга. Вот чем отличается окружность от круга.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

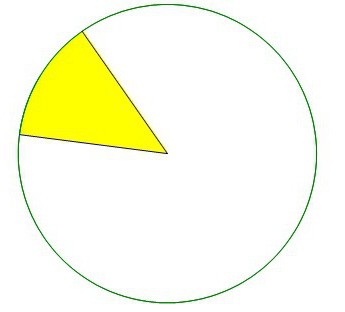
Что такое сектор?
Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.
Предмет, отображаемый этим понятием, может иметь только круг. Окружность (радиус тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.
Видео:Математика это не ИсламСкачать

Выводы
Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих геометрических фигур, является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
Видео:Длина окружности. Математика 6 класс.Скачать

Круг и окружность в нашей жизни
Под задачей с практическим содержанием понимается математическая задача, которая раскрывает приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомит с её использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| mou_shatkovskaya_oshkrug.pptx | 2.01 МБ |
| pechatnoe_krug_i_okr_konfer2019.docx | 2.69 МБ |
Предварительный просмотр:
Видео:7 класс, 21 урок, ОкружностьСкачать

Подписи к слайдам:
МОУ « Шатковская ОШ» Научно – практическая конференция по математике на тему: «Решение задач с практическим содержанием» «Круг и окружность в нашей жизни» Выполнила: ученица 8 класса Антропова Юлия Руководитель: учитель математики Кадяева Елена Михайловна
Введение Под задачей с практическим содержанием понимается математическая задача, которая раскрывает приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомит с её использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций. Рассматривая задачи с практическим содержанием на уроках математики, ученикам прививается интерес к предмету. Необходимо, чтобы каждое новое понятие или положение находило применение в задачах практического характера, в реальной жизни. Именно это убеждает учащиеся, что математические знания им нужны в жизни для решения многих практических задач и математика наука полезная, необходимая во всех видах деятельности. Важное значение в процессе обучения математике имеет понимание школьниками значимости учебного материала, перспективы его использования. Я решила провести обобщение доступных задач с практическим содержанием на применение понятий окружности и круга.
Окружность Окружность – удивительно гармоническая фигура, древние греки считали её самой совершенной. Совершенство окружности – в расположении всех её точек на одинаковом расстоянии от центра. Окружность – единственная кривая, которая может «скользить сама по себе», вращаясь вокруг центра.
Круг Круг – это часть плоскости, ограниченная окружностью.
Практические задачи повседневной жизни, которые используют знания о круге и окружности. Знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни: разбить клумбу или фонтан, сшить головной убор, связать салфетку, сделать круглую крышу, окно или крышку, ёлочную игрушку, сделать выкройку платья или юбки, нарисовать узор и т.п.
Задача №1 Почему канализационные люки делают круглыми, а не квадратными? Ответ: сравните сторону квадрата с его диагональю. Квадратная крышка может провалиться в люк, чего никогда не случится с круглой крышкой.
Задача №2 Диаметр основания Царь — колокола, находящегося в Московском Кремле, равен 6,6м Найдите площадь основания колокола.
Задача №3 Длина окружности цирковой арены равна 41м. Найдите диаметр и площадь арены.
Задача №4 Вокруг круглой клумбы, радиус которой равен 3м,проложена дорожка шириной 1м. Сколько нужно песка, чтобы посыпать дорожку, если на 1м кв. дорожки требуется 0,8 дм. куб. песка?
Колесо Одно из главных применений круга – это колесо. Это одно из самых великих изобретений человечества. Додуматься до колеса было не так просто, как это может показаться. Ведь даже ацтеки, жившие в Мексике, почти до 16 века не знали колеса. Сколько разных машин и механизмов! Есть у них у всех схожие части – детали, и одна из них – колесо.
Задача Автомобиль прошёл 989м. Найдите диаметр колеса автомобиля, если известно, что оно сделало 500 оборотов.
Решение — Что означает один оборот колеса с математической точки зрения? -Чему равно расстояние, пройденное автомобилем, если колесо автомобиля сделало один оборот? 500*2πR=989, то d =2 R = Ответ: 63см
« Математика владеет не только истинной, но и красотой…» Бертран Рассел
Архитектура Окружность как совершенная геометрическая форма всегда привлекала к себе внимание художников, архитекторов
Ворота Таврического дворца В неповторимом архитектурном облике Санкт-Петербурга восторг и удивление вызывает «чугунное кружево» — садовые ограды, перила мостов и набережных, балконные решётки, фонари. Особую воздушность придают воротам окружности, сплетенные в орнамент.
К.Росси. Арка Главного штаба. С. — Петербург Торжественность и устремлённость ввысь – такой эффект в архитектуре зданий достигается использованием арок, представляющих дуги окружностей
Витраж собора св. Витта. Прага Окружности и дуги являются основными элементами готических храмов средневековья.
Архангельский собор. Москва Архитектура православных церквей включает в себя как обязательные элементы купола, арки, округлые своды, что зрительно увеличивает пространство, создаёт эффект полёта, лёгкости.
Заключение Задачи с практическим содержанием целесообразно использовать в процессе обучения для раскрытия многообразия применений математики в жизни, своеобразия отражения ею реального мира и формирования практических умений и навыков.
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Исследовательская работа «Круг в нашей жизни»
Разделы: Математика
Круг и окружность – одни из самых древнейших геометрических фигур, философы древности придавали им большое значение. Круг – воплощение нескончаемого Времени и Пространства, символ всего сущего, Вселенной. “Из всех фигур прекраснейшая – круг”, – считал Пифагор.
Вокруг нас много круглых предметов. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезло все круглое! Казалось бы – пусть все будет квадратным. Разве нельзя прожить без круглых труб, а к квадратным колесам нельзя привыкнуть? Можно ли вообще представить жизнь человека без использования круга? Почему так много тел имеют круглую форму? Чтобы найти ответы на все эти вопросы, в первую очередь, необходимо рассмотреть историю возникновения этих понятий и дальнейшее их развитие.
История возникновения и развития геометрических понятий “круг” и “окружность”.
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. Специальных названий для геометрических фигур, конечно, не было. Говорили: “такой же, как кокосовый орех” или “такой же, как соль” и т.д. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими фигурами.
Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки. Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо. К сожалению, неизвестен непосредственный изобретатель колеса.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму. Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания.
Математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой. В Древней Греции все разрозненные знания привели в систему, геометрия стала бурно развиваться как наука. Только в Древней Греции “окружность” и “круг” получили свои названия, почти все названия геометрических фигур греческого происхождения, как и само слово геометрия (“гео” – земля, а “метрио” – мерить). Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.
В Древней Греции многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны. Наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах “Начала”. В течение многих веков “Начала” были единственной учебной книгой, по которой молодежь изучала геометрию. И даже сейчас, в наше время, учебники написаны под большим влиянием “Начал” Евклида.
Окружность и круг – это плоские фигуры . Мы живем в мире трех измерений. А в какое геометрическое тело превратятся окружность и круг, если попадут в пространство? Это сфера и шар. “Сфера” – произошло от греческого слова “сфайра”, в переводе – “мяч”. Кроме этого геометрия пространства рассматривает и другие круглые тела – это “цилиндр” (от греческого слова “кюлиндрос”, что означает “валик”, “каток”) и “конус” (от греческого слова “конос”, означающего “сосновая шишка”). Самым важным среди круглых тел был шар.
Итак, в Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса (Приложение 5). (Приложение 2).
Круг – “циркулус” – латинское слово, от него же и “циркуль”, без которого бы мы не построили круг. Циркуль и линейка – самые старые чертежные инструменты на Земле. (Приложение 3.)
Элементы окружности и круга (Приложение 2):
Радиус окружности – это отрезок, соединяющий центр окружности с любой ее точкой (по-латыни – спица колеса).
Диаметр окружности – это хорда, проходящая через центр окружности (с греческого – “поперечник”).
Хорда окружности – отрезок, соединяющий любые две точки на окружности (с греческого– “струна”).
Дуга окружности – это часть окружности, ограниченная двумя точками.
Часто в практических задачах нужно узнать длину окружности. А как измерить длину окружности, если сама окружность – кривая линия, а единица измерения длины – отрезок? Есть несколько способов измерения длины окружности (Приложение 1).
Однако эти способы непосредственного измерения длины окружности малоудобны и дают приближенные результаты. Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость: С:d ≈ 3,1.
Многие ученые – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, его стали обозначать греческой буквой π-ο ервая буква греческого слова “периферия” – круг.
С:d = π, где С – длина окружности, d – длина диаметра, отсюда и формула длины окружности C = πd или C = 2πr.
Изучив исследования ученых математиков, мы провели следующие измерения и вычисления:
1. Вычисление числа пи : а) с помощью тонкой нити измерили длину окружности С некоторых предметов быта; б) чтобы точнее найти длину диметра d, приложили этот предмет к листу бумаги и обвели карандашом, вырезали, свернули пополам, линия сгиба – это диаметр, измерили его с помощью линейки; в) нашли отношение С:d, данные занесли в таблицу:
| Предметы | Длина окружности С | Диаметр d | Отношение С:d |
| Стакан | 22 см | 7 см | 3.1428 |
| Ведро | 82 см | 26 см | 3.1538 |
| Тарелка | 62 см | 19,5 см | 3,1794 |
| Кастрюля | 69 см | 22 см | 3.1363 |
| Бидон | 52 см | 16,5 см | 3,1515 |
2. Границы значения числа пи: а) с помощью циркуля вписали круг в квадрат: если диаметр равен 1,то длина окружности равна π . Периметр квадрата со стороной 1 равен 4. Значит π меньше 4. (Приложение 6. Рис.1). б) в этот же круг вписали правильный шестиугольник: диаметр круга снова 1, длина окружности равна π . Сторона правильного шестиугольника равна радиусу, т.е.0,5,а периметр равен 6·0,5=3,значит π больше 3 (Приложение 6. Рис.2).
В результате мы убедились, что отношение длины окружности к ее диаметру (число π) есть число постоянное и 3 ‹ π ‹ 4 ,т.е. мы подтвердили исследования ученых – математиков.
Одна из загадок числа π состоит в том, что оно не может быть выражено какой – либо точной дробью. История числа π достойна восхищения, многие математики затратили на его вычисления не один десяток лет. Уточнялись нижняя и верхняя оценки числа и предпринимались неудачные попытки представить π в виде дроби и, таким образом, окончательно найти его значение (Приложение 4). Пока рекорд принадлежит японскому математику, в 2004 году – Ясума Канада из Токио рассчитал число π на компьютере до 1,24 триллиона знаков.
π -3,141 592 653 589 793 238 462 643 383279 502 884197 169 399 375 105 ….
Зачем нужно π, да еще с такой точностью? Число π чрезвычайно важно для ученых и инженеров. Все, что круглое и все, что движется по кругу (как колеса или планеты), содержит π. Без π люди не могли создать автомобили, понять движение планет или сосчитать сколько гороха поместится в консервную банку. Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, и, по-прежнему, волнует ученых. В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Все это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.
Изучив литературу и проделав собственные измерительные исследования с окружностью и кругом, мы пришли к следующим выводам: окружность и круг – это удивительно гармоничные фигуры. Окружность – единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра. Это свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль, и почему колеса делают круглыми, а не квадратными или треугольными.
Круг в окружающей жизни.
Исследуя вопрос о роли круга в окружающей жизни, мы провели анкетирование обучающихся 5-9 классов и педагогов МО ШИСП (всего 90 человек):
- Какие круглые тела вы встречаете в окружающей жизни?
- Какое значение имеет круг в других науках?
- Какие практические задачи повседневной жизни решаются, используя знания о круге и окружности?
- Как вы считаете, почему встречается так много круглых тел в природе?
Ответы на первый вопрос представлены в презентации.
Из ответов учителей – предметников на второй вопрос анкеты мы поняли, что круг имеет большое значение не только в математике, но и в других науках:
| Предмет | Использование |
| Физика и астрономия | Движение небесных тел происходит по круговым орбитам. Зодиакальный круг, астрономический круг. Круг с точкой в центре символизирует солнце. |
| География | Меридианы и параллели, определяющие положение тела на земном шаре, экватор. Круговые процессы-циклы: круговорот воды и веществ в природе. Смена времен года, смена дня и ночи. |
| Химия | Строение атома: ядро круглое, электроны вращаются вокруг ядра по круговым орбитам. |
| Биология | У всех клеток есть круглое ядро. Круглую форму имеют клетки крови, цилиндрическую – клетки многих желез. Стебли растений и стволы деревьев, кости человека – круглые. Кровообращение идет по кругу. Овощи и фрукты имеют шарообразную или конусовидную форму. Цикличность развития живых существ. |
| Русский язык | В русском языке слово “круглый” означает высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”. От слова круг образовано множество различных слов: круглый, кругленький, округлить, округлиться, округлый, кругом, вокруг, окружать, кружить и многое другое. Округлые формы, круглое лицо, кругленькие щеки, круглый год, голова идет кругом, ходить по кругу – часто употребляемые выражения. |
| История и обществознание | “Круглый стол” – конференции, кругооборот капитала, круг семьи , колесо истории, “большой и малый круг истории” – исторические циклы. |
Проанализировав ответы на третий вопрос анкеты, мы поняли, что знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни: разбить клумбу или фонтан, сделать круглую крышу, окно или крышку, сшить головной убор, связать салфетку, сделать елочную игрушку, сделать выкройку платья или юбки, нарисовать узор и т.п.
Таким образом, круг в жизни человека имеет очень важную роль, и в жизни без круглых предметов обойтись невозможно.
Не все, кого мы анкетировали, смогли дать ответ на четвертый вопрос.
Здесь мы помещаем самые интересные и распространенные ответы:
- Только круглые предметы могут катиться, и поэтому их легче перемещать.
- Потому что, куда бы мы не пошли, мы возвращаемся, т.е. идем по кругу.
- У круга нет углов, и поэтому он удобен в применении, например, круглые монеты не могут порвать карман, о них не уколешься, не порежешься.
- Мячик не может быть квадратным, он не будет отпрыгивать.
- Посуду делали из глины, и округлую форму было легче придать, чем квадратную. Круглую посуду легче мыть, не надо выскребать из углов, в ней удобней размешивать.
- Легче изготовить круглое, чем угловатое. Многие технические процессы легче для тел вращения.
- На круглую форму идет меньше материала, чем на квадратную.
- Круглая крышка люка никогда не провалится, в отличие от квадратной.
- Все банки и крышки круглой формы, т.к. каждая точка окружности является точкой концентрации напряжения, и ее легко открыть, у прямоугольной формы такими точками являются только углы.
- Потому ,что солнце круглое, а без солнца мы не могли бы существовать.
- Круглая форма универсальна в природе.
Почему же на самом деле встречается так много круглых тел? Мы обратились к научным источникам. На этот вопрос можно ответить, рассмотрев мыльный пузырь, т.к. он идеально круглой формы. Силы поверхностного натяжения не дают лопнуть мыльному пузырю и стремятся придать мыльному пузырю максимально компактную форму. Самая компактная форма в природе – это шар. При шарообразной форме воздух внутри пузыря равномерно давит на все участки его внутренней стенки.
В небе много круглых объектов: Солнце, Луна, планеты, звезды. Почему не быть хотя бы одной некруглой планете? Ну, пусть одна, будет кубическая или пирамидальная. Но это невозможно? Есть сила, которая во всей Вселенной превращает миры в гладкие шары. Эта сила – сила тяготения. Каждый предмет имеет свою гравитацию, притягивает к себе другие тела, а также и свои части. Чем больше тело, тем сила тяжести увеличивается. Земля наша огромная, поэтому она имеет свою большую силу тяжести, которая заставляет притягиваться все к ее центру, а тело преобразовываться в шар. Если бы в силу каких-то причин удалось изменить нашу планету и придать ей иную форму, не шара, то спустя некоторое время она снова стала бы шарообразной. С телами на земле это не происходит, потому что их сила очень маленькая и сила тяжести Земли препятствует этому. Но если взять, например, каплю воды и запустить в космос, она сразу же преобразуется в шар. Именно жидкость способна преобразовываться в шарообразную форму. Земля состоит в основном из магмы (жидкости) поэтому и имеет форму шара.
Таким образом, мы пришли к выводам, что сама природа выбирает эту удобную и компактную форму – шара.
Кроме того, окружность и круг в виде сферы и шара – самая распространенная форма во Вселенной.
Круг и окружность – это еще и траектория движения Земли вокруг Солнца, это перемещение звезд на небе, это цикличность всех процессов, происходящих в мире. Если бы необходимо было бы выбрать форму, наиболее точно передающую устройство мира, то это были бы окружность и круг.
Изучив научную литературу, мы сделали вывод, что с незапамятных времен люди используют в своей жизни круг.
1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).
2. Мы не можем представить свою жизнь без машин: автобус, трактор, велосипед, швейная, стиральная и пишущая машинки, самолет, вездеход, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес. Зубчатые колеса спрятаны внутри многих машин, одно колесо заставляет вращаться другое, колеса с желобком –блоки, помогающие поднимать тяжелые грузы. Машины из века в век совершенствовались и совершенствуются, но неизменным остается использование в них колеса, как основной детали.
3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений, у многих народов символизирующая динамизм и бесконечное движение в противовес квадратам домов, участкам земли и городам оседлых и зерносеющих народов. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.
4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир (Приложение 7).
Есть в математике задачи, которые до сих пор не разрешены, например, знаменитая задача о “квадратуре круга” – о построении квадрата, равновеликого данному кругу и т.д.
5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль (Приложение 8).
6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство, бесконечность, отсутствие начала и конца, верха и низа, цикличность, повторяемость, завершенность. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду; небесные миры, землю и преисподнюю; фазы луны; восходящее, полуденное и заходящее солнце. Многие народы используют круг в религии, как символ связи земного с космосом.
В последнее время в разных местах земного шара стали появляться круги на полях, которые создают посланцы иных миров, желая о чем-то предупредить землян. (Приложение 9).
7. В энциклопедии мы нашли еще много понятий связанных с кругом: кругловязальная машина, круглочулочный автомат, круглогубцы, кругломер, “круговая система” в спорте, кругозор, круг друзей, круг общения, спасательный круг, святой круг, спиритический круг, круговая оборона, круговая порука, круглосуточная аптека, круги вокруг глаз.
- Круг в жизни человека имеет очень важную роль, и без использования круглых предметов обойтись невозможно.
- Окружность и круг – удивительно гармоничные, совершенные, простые фигуры. Окружность – единственная замкнутая кривая, которая может “скользить сама по себе”, вращаясь вокруг центра, поэтому колеса делают круглыми, а не квадратными или треугольными.
- Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы.
- Круг – символ цикличности, повторяемости. Все движется по кругу.
- Круг дает ощущение взаимосвязи с Космосом.
- Сама природа выбирает эту удобную и компактную форму как шар и круг.
📸 Видео
Окружность. Круг. 5 класс.Скачать

Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Круг. Окружность | Математика 3 класс #21 | ИнфоурокСкачать

КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

МАТЕМАТИКА 5 класс: Окружность и кругСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Не каждый знает как найти центр окружности без циркуля! #ShortsСкачать