Применение касательной к окружности в жизни человека

Секущие, касательные — все это сотни раз можно было слышать на уроках геометрии. Но выпуск из школы позади, проходят года, и все эти знания забываются. Что следует вспомнить?

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Сущность

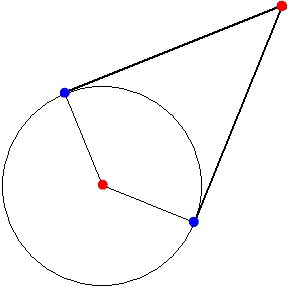
Термин «касательная к окружности» знаком, наверное, всем. Но вряд ли у всех получится быстро сформулировать его определение. Между тем касательной называют такую прямую, лежащую в одной плоскости с окружностью, которая пересекает ее только в одной точке. Их может существовать огромное множество, но все они обладают одинаковыми свойствами, о которых речь пойдет ниже. Как нетрудно догадаться, точкой касания называют то место, где окружность и прямая пересекаются. В каждом конкретном случае она одна, если же их больше, то это будет уже секущая.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

История открытия и изучения

Понятие касательной появилось еще в древности. Построение этих прямых сначала к окружности, а потом к эллипсам, параболам и гиперболам с помощью линейки и циркуля проводилось еще на начальных этапах развития геометрии. Разумеется, история не сохранила имя первооткрывателя, но очевидно, что еще в то время людям были вполне известны свойства касательной к окружности.

В Новое время интерес к этому явлению разгорелся вновь — начался новый виток изучения этого понятия в сочетании с открытием новых кривых. Так, Галилей ввел понятие циклоиды, а Ферма и Декарт построили к ней касательную. Что же касается окружностей, кажется, еще для древних не осталось секретов в этой области.

Видео:Построение касательной к окружностиСкачать

Свойства

Радиус, проведенный в точку пересечения, будет перпендикулярен прямой. Это

Из вышесказанного есть важное следствие. Для каждой точки окружности можно построить касательную, но при этом только одну. Доказательство этого достаточно просто: теоретически опустив на нее перпендикуляр из радиуса, выясняем, что образованный треугольник существовать не может. И это значит, что касательная — единственная.

Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Построение

Среди прочих задач по геометрии есть особая категория, как правило, не

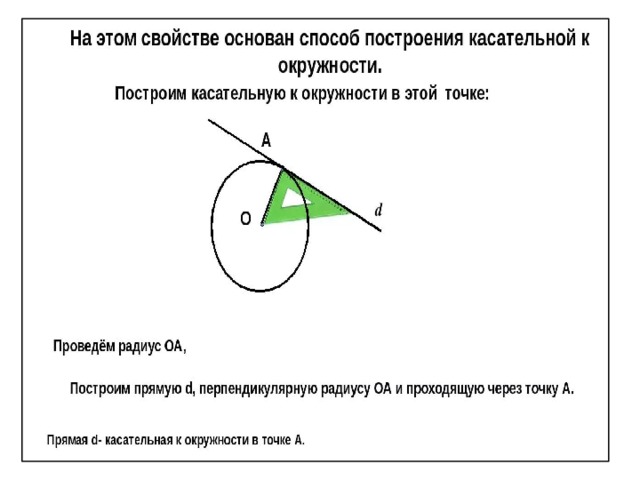
Итак, даны окружность и точка, лежащая вне ее границ. И необходимо провести через них касательную. Как же это сделать? Прежде всего, нужно провести отрезок между центром окружности О и заданной точкой. Затем с помощью циркуля следует разделить его пополам. Чтобы это сделать, необходимо задать радиус — чуть более половины расстояния между центром изначальной окружности и данной точкой. После этого нужно построить две пересекающиеся дуги. Причем радиус у циркуля менять не надо, а центром каждой части окружности будут изначальная точка и О соответственно. Места пересечений дуг нужно соединить, что разделит отрезок пополам. Задать на циркуле радиус, равный этому расстоянию. Далее с центром в точке пересечения построить еще одну окружность. На ней будет лежать как изначальная точка, так и О. При этом будет еще два пересечения с данной в задаче окружностью. Именно они и будут точками касания для изначально заданной точки.

Видео:Построение касательной к окружностиСкачать

Интересное

Именно построение касательных к окружности привело к рождению

Кроме того, касательная к окружности связана с геометрическим смыслом тангенса. Именно от этого и происходит его название. В переводе с латыни tangens — «касательная». Таким образом, это понятие связано не только с геометрией и дифференциальным исчислением, но и с тригонометрией.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

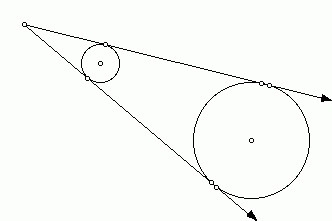
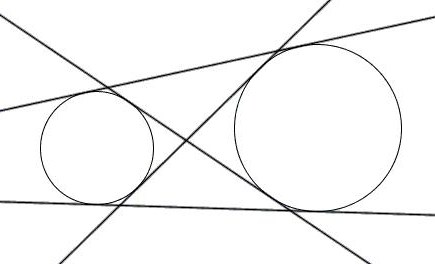
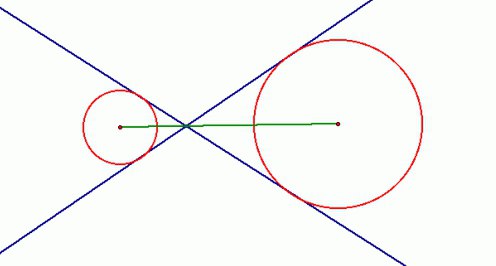
Две окружности

Не всегда касательная затрагивет лишь одну фигуру. Если к одной окружности можно провести огромное множество прямых, то почему же нельзя наоборот? Можно. Вот только задача в этом случае серьезно усложняется, ведь касательная к двум окружностям может проходить не через любые точки, а взаимное расположение всех этих фигур может быть очень

Видео:Касательные к окружностиСкачать

Типы и разновидности

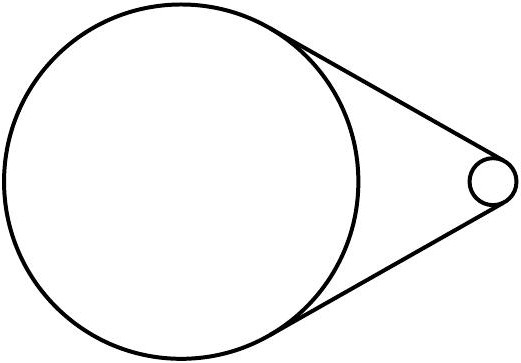
Когда речь идет о двух окружностях и одной или нескольких прямых, то даже если известно, что это касательные, не сразу становится ясно, как все эти фигуры расположены по отношению друг к другу. Исходя из этого, различают несколько разновидностей. Так, окружности могут иметь одну или две общие точки или не иметь их вовсе. В первом случае они будут пересекаться, а во втором — касаться. И вот тут различают две разновидности. Если одна окружность как бы вложена во вторую, то касание называют внутренним, если нет — то внешним. Понять взаимное расположение фигур можно не только, исходя из чертежа, но и располагая информацией о сумме их радиусов и расстоянии между их центрами. Если две эти величины равны, то окружности касаются. Если первая больше — пересекаются, а если меньше — то не имеют общих точек.

Так же и с прямыми. Для любых двух окружностей, не имеющих общих точек, можно

Если речь идет об окружностях, которые имеют одну общую точку, то задача серьезно упрощается. Дело в том, что при любом взаимном расположении в этом случае касательная у них будет только одна. И проходить она будет через точку их пересечения. Так что построение трудности не вызовет.

Если же фигуры имеют две точки пересечения, то для них может быть построена прямая, касательная к окружности как одной, так и второй, но только внешняя. Решение этой проблемы аналогично тому, что будет рассмотрено далее.

Видео:Построение касательной к окружности.Скачать

Решение задач

Как внутренняя, так и внешняя касательная к двум окружностям, в построении не так уж просты, хоть эта проблема и решаема. Дело в том, что для этого используется вспомогательная фигура, так что додуматься до такого способа самостоятельно

Прежде всего, около центра большей окружности нужно построить вспомогательную. При этом на циркуле должна быть установлена разница между радиусами двух изначальных фигур. Из центра меньшей окружности строятся касательные к вспомогательной. После этого из О1 и О2 проводятся перепендикуляры к этим прямым до пересечения с изначальными фигурами. Как следует из основного свойства касательной, искомые точки на обеих окружностях найдены. Задача решена, по крайнем мере, ее первая часть.

Для того чтобы построить внутренние касательные, придется решить практически

Касательная к окружности или даже двум и больше — не такая уж сложная задача. Конечно, математики давно перестали решать подобные проблемы вручную и доверяют вычисления специальным программам. Но не стоит думать, что теперь необязательно уметь делать это самостоятельно, ведь для правильного формулирования задания для компьютера нужно многое сделать и понять. К сожалению, есть опасения, что после окончательного перехода на тестовую форму контроля знаний задачи на построение будут вызывать у учеников все больше трудностей.

Что же касается нахождения общих касательных для большего количества окружностей, это не всегда возможно, даже если они лежат в одной плоскости. Но в некоторых случаях можно найти такую прямую.

Видео:КАСАТЕЛЬНАЯ к ОКРУЖНОСТИ 8 класс геометрия АтанасянСкачать

Примеры из жизни

Общая касательная к двум окружностям нередко встречается и на практике, хоть это и не всегда заметно. Конвейеры, блочные системы, передаточные ремни шкивов, натяжение нити в швейной машинке, да даже просто велосипедная цепь — все это примеры из жизни. Так что не стоит думать, что геометрические задачи остаются лишь в теории: в инженерном деле, физике, строительстве и многих других областях они находят практическое применение.

Видео:Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Касательная к окружности

Данная презентация дает наглядное представление о касательной к окружности.Ученики наглядно видят области применения касательной: в архитектуре. в медицине .в машиностроении и т. д.

Просмотр содержимого документа
«Касательная к окружности»

Урок математики в 6 б классе

Из опыта работы учителя математики МБОУ «Гимназия№11» Гусейновой А.Г.

1.Изучение понятия касательной к окружности, свойства касательной.

2. Применение новых знаний к решению задач, связанных с конкретными ситуациями.

3. Формирование у обучающихся системы научных знаний.

4.Совершенствование умений запоминать, выделять главное.

5.Формирование представлений о значимости.

Совершенствование умений в решении практических задач.

6. Совершенствование умений и навыков в решении исследовательских задач.

1. Скорость скутера по течению реки — 27 км/ч, а против течения — 24 км/ч. Чему равна скорость течения реки? (1,5 км/ч)

2. Катя и Сергей одновременно отправились навстречу друг другу. Катя идёт пешком со скоростью 4 км/ч, а Сергей едет на велосипеде со скоростью, в 2 раза большей. Через какое время ребята встретятся, если первоначально расстояние между ними было 3 км? (через 15 минут)

3,6 • 3; 5,1: 3; 2,8: 7; 0,36: 9; 0,012: 4.

4. Как изменится положение запятой в десятичной дроби, если: а) эту дробь уменьшить в 100 раз; б) эту дробь увеличить в 1000 раз;

в) эту дробь сначала уменьшить в 10 раз, а потом увеличить в 100 раз?

Устный опрос по теме.

На экране будут появляться элементы окружности (круга). Вам нужно их узнать и дать им определения.

Окружность – множество точек на плоскости, равноудаленных от данной точки – центра окружности.

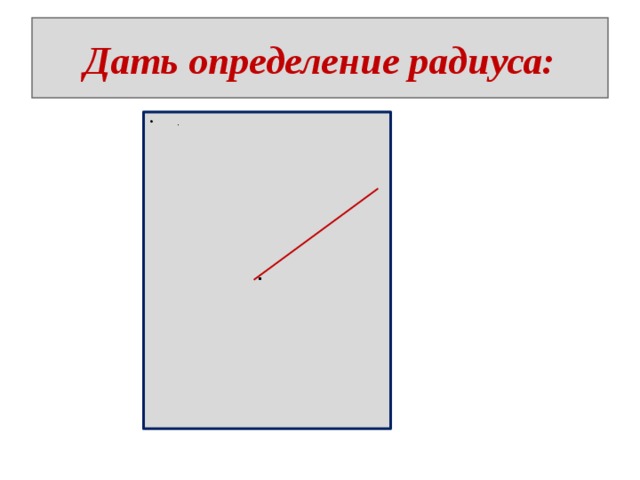
Дать определение радиуса:

Радиус – это отрезок, соединяющий центр окружности с любой точкой окружности.

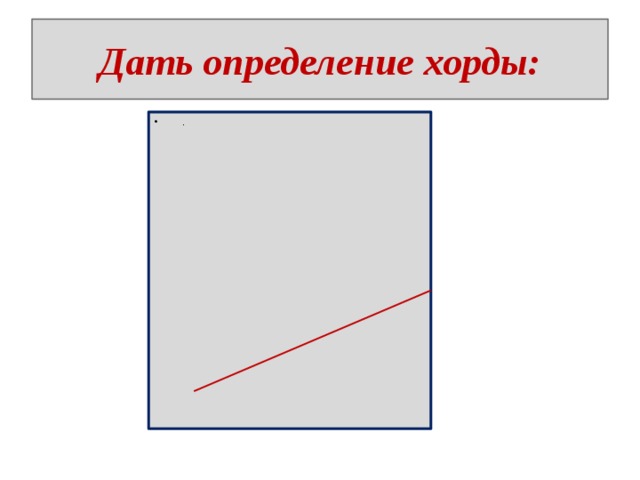
Дать определение хорды:

• .

Хорда – это отрезок, соединяющий две точки окружности.

Дать определение диаметру:

• .

Диаметр – это отрезок, соединяющий две точки окружности и проходящий через ее центр.

Дать определение дуги окружности:

• .

Дуга – это часть окружности, ограниченная двумя точками.

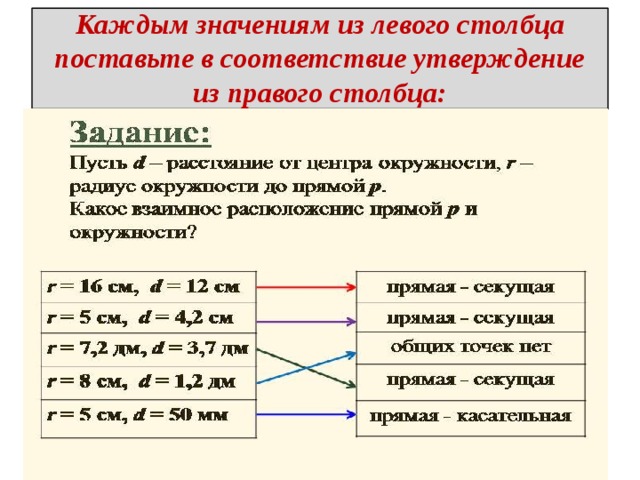
Каждым значениям из левого столбца поставьте в соответствие утверждение из правого столбца:

— Мы устали чуточку, отдохнем минуточку.

— Кто согласен с тем, что «Прямая является касательной по отношению к окружности, если она имеет одну общую точку с ней». – встаньте.

— Нарисуйте глазками окружность, а теперь головой, туловищем.

-Улыбнитесь соседу справа, улыбнитесь соседу слева.

— Молодцы, тихонечко садитесь.

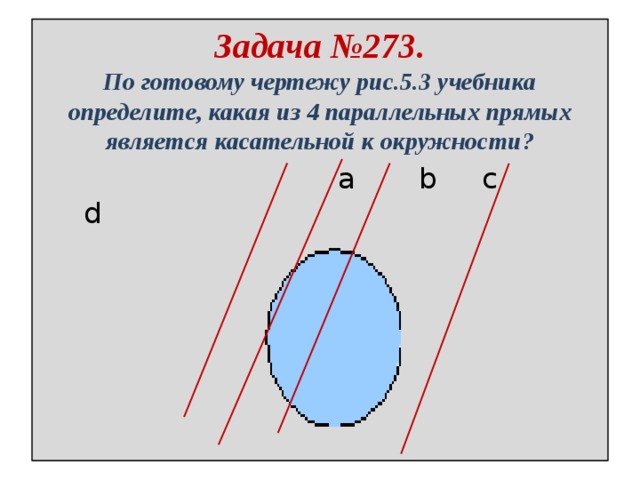
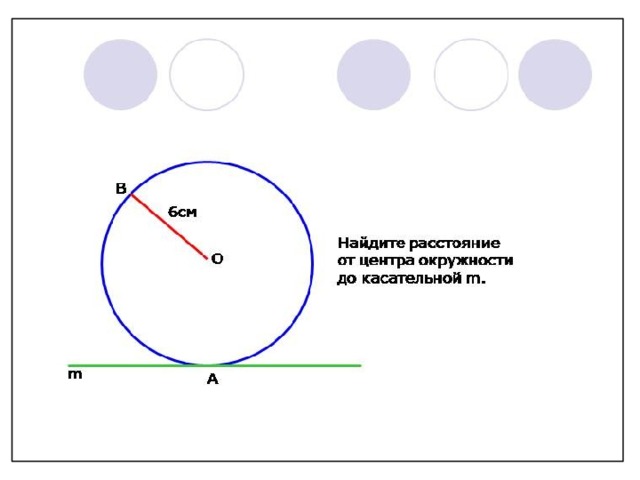
Задача №273. По готовому чертежу рис.5.3 учебника определите, какая из 4 параллельных прямых является касательной к окружности?

Прямая b является касательной, так как она имеет с окружностью одну общую точку.

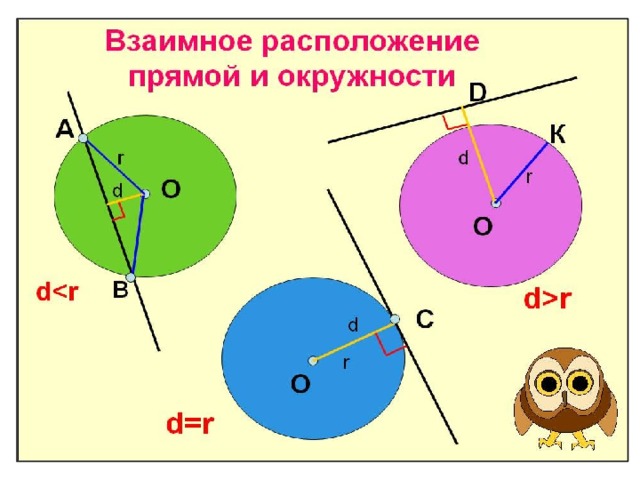
В таблице даны радиус окружности и расстояние от центра этой окружности до некоторой прямой. Что можно сказать о взаимном расположении прямой и окружности в каждом случае? Проверьте себя, выполнив построения.

Условие задачи в виде таблицы записано на доске.

Радиус окружности в см

Расстояние от центра окружности до прямой в см

Прямая пересекает окружность(Секущая)

Прямая касается окружности(Касательная)

Прямая не пересекает окружность(не пересекающая)

Проведите прямую и отметьте на ней произвольную точку М. Постройте несколько окружностей разных радиусов, касающихся данной прямой в точке М. Где лежат центры таких окружностей?

Из истории математики

Определение касательной впервые встречается в учебнике «Элементы геометрии» французского математика Лежандра, написанного в конце 19 века. А то, что касательная перпендикулярна к радиусу, проведенному в точку касания, было уж известно греческому ученому Архиту Тарентскому, жившему в 4 веке до н.э.

Касательная к окружности нередко встречается и на практике, хоть это и не всегда заметно. Конвейеры, блочные системы, передаточные ремни шкивов, натяжение нити в швейной машинке, да даже просто велосипедная цепь — все это примеры из жизни. Так что не стоит думать, что геометрические задачи остаются лишь в теории: в инженерном деле, физике, медицине, строительстве и многих других областях они находят практическое применение.

— Как располагаются прямая и плоскость?

— Какая прямая называется касательной к окружности?

— Сколько касательных можно провести через данную на окружности точку?

— Сколько всего касательных существует у окружности?

Оцените урок и результат своей деятельности. Выберите один из вариантов:

На уроке я работал активно / пассивно.

Своей работой на уроке я доволен / недоволен.

Урок для меня показался коротким / длинным

За урок я устал / не устал

Материал урока мне был понятен / не понятен

Видео:Секретная теорема из учебника геометрииСкачать

Применение касательной к окружности

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Касательная к окружности

Данная презентация дает наглядное представление о касательной к окружности.Ученики наглядно видят области применения касательной: в архитектуре. в медицине .в машиностроении и т. д.

Просмотр содержимого документа
«Касательная к окружности»

Урок математики в 6 б классе

Из опыта работы учителя математики МБОУ «Гимназия№11» Гусейновой А.Г.

1.Изучение понятия касательной к окружности, свойства касательной.

2. Применение новых знаний к решению задач, связанных с конкретными ситуациями.

3. Формирование у обучающихся системы научных знаний.

4.Совершенствование умений запоминать, выделять главное.

5.Формирование представлений о значимости.

Совершенствование умений в решении практических задач.

6. Совершенствование умений и навыков в решении исследовательских задач.

1. Скорость скутера по течению реки — 27 км/ч, а против течения — 24 км/ч. Чему равна скорость течения реки? (1,5 км/ч)

2. Катя и Сергей одновременно отправились навстречу друг другу. Катя идёт пешком со скоростью 4 км/ч, а Сергей едет на велосипеде со скоростью, в 2 раза большей. Через какое время ребята встретятся, если первоначально расстояние между ними было 3 км? (через 15 минут)

3,6 • 3; 5,1: 3; 2,8: 7; 0,36: 9; 0,012: 4.

4. Как изменится положение запятой в десятичной дроби, если: а) эту дробь уменьшить в 100 раз; б) эту дробь увеличить в 1000 раз;

в) эту дробь сначала уменьшить в 10 раз, а потом увеличить в 100 раз?

Устный опрос по теме.

На экране будут появляться элементы окружности (круга). Вам нужно их узнать и дать им определения.

Окружность – множество точек на плоскости, равноудаленных от данной точки – центра окружности.

Дать определение радиуса:

Радиус – это отрезок, соединяющий центр окружности с любой точкой окружности.

Дать определение хорды:

Хорда – это отрезок, соединяющий две точки окружности.

Дать определение диаметру:

Диаметр – это отрезок, соединяющий две точки окружности и проходящий через ее центр.

Дать определение дуги окружности:

Дуга – это часть окружности, ограниченная двумя точками.

Каждым значениям из левого столбца поставьте в соответствие утверждение из правого столбца:

— Мы устали чуточку, отдохнем минуточку.

— Кто согласен с тем, что «Прямая является касательной по отношению к окружности, если она имеет одну общую точку с ней». – встаньте.

— Нарисуйте глазками окружность, а теперь головой, туловищем.

-Улыбнитесь соседу справа, улыбнитесь соседу слева.

— Молодцы, тихонечко садитесь.

Задача №273. По готовому чертежу рис.5.3 учебника определите, какая из 4 параллельных прямых является касательной к окружности?

Прямая b является касательной, так как она имеет с окружностью одну общую точку.

В таблице даны радиус окружности и расстояние от центра этой окружности до некоторой прямой. Что можно сказать о взаимном расположении прямой и окружности в каждом случае? Проверьте себя, выполнив построения.

Условие задачи в виде таблицы записано на доске.

Радиус окружности в см

Расстояние от центра окружности до прямой в см

Прямая пересекает окружность(Секущая)

Прямая касается окружности(Касательная)

Прямая не пересекает окружность(не пересекающая)

Проведите прямую и отметьте на ней произвольную точку М. Постройте несколько окружностей разных радиусов, касающихся данной прямой в точке М. Где лежат центры таких окружностей?

Из истории математики

Определение касательной впервые встречается в учебнике «Элементы геометрии» французского математика Лежандра, написанного в конце 19 века. А то, что касательная перпендикулярна к радиусу, проведенному в точку касания, было уж известно греческому ученому Архиту Тарентскому, жившему в 4 веке до н.э.

Касательная к окружности нередко встречается и на практике, хоть это и не всегда заметно. Конвейеры, блочные системы, передаточные ремни шкивов, натяжение нити в швейной машинке, да даже просто велосипедная цепь — все это примеры из жизни. Так что не стоит думать, что геометрические задачи остаются лишь в теории: в инженерном деле, физике, медицине, строительстве и многих других областях они находят практическое применение.

— Как располагаются прямая и плоскость?

— Какая прямая называется касательной к окружности?

— Сколько касательных можно провести через данную на окружности точку?

— Сколько всего касательных существует у окружности?

Оцените урок и результат своей деятельности. Выберите один из вариантов:

На уроке я работал активно / пассивно.

Своей работой на уроке я доволен / недоволен.

Урок для меня показался коротким / длинным

За урок я устал / не устал

Материал урока мне был понятен / не понятен

Видео:Секущая и касательная. 9 класс.Скачать

Касательная к окружности

О чем эта статья:

Видео:Касательная к окружности | Геометрия 7-9 класс #69 | ИнфоурокСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

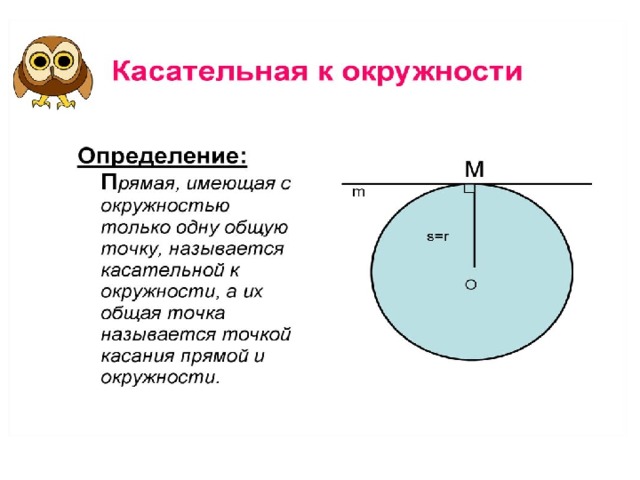
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:#59. Олимпиадная задача о касательной к окружности!Скачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

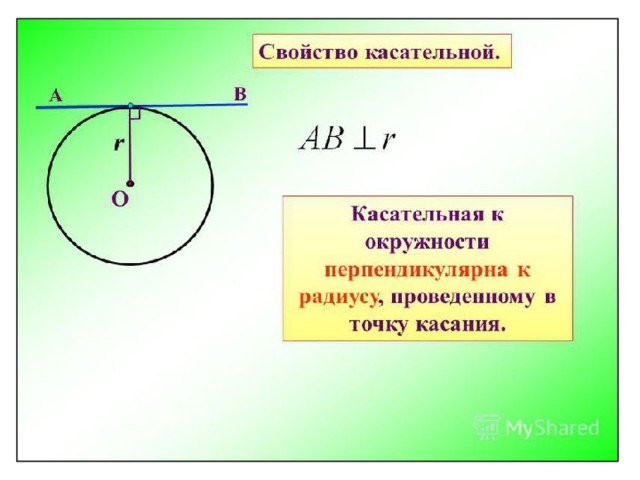
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Видео:Касательная к окружности и её свойстваСкачать

Касательная к окружности

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.

. Угол равен , где — центр окружности. Его сторона касается окружности. Найдите величину меньшей дуги окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол — прямой. Из треугольника получим, что угол равен градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги — тоже градуса.

. Найдите угол , если его сторона касается окружности, — центр окружности, а большая дуга окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.

Это чуть более сложная задача. Центральный угол опирается на дугу , следовательно, он равен градусов. Тогда угол равен . Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол — прямой. Тогда угол равен .

. Хорда стягивает дугу окружности в . Найдите угол между этой хордой и касательной к окружности, проведенной через точку . Ответ дайте в градусах.

Проведем радиус в точку касания, а также радиус . Угол равен . Треугольник — равнобедренный. Нетрудно найти, что угол равен градуса, и тогда угол равен градусов, то есть половине угловой величины дуги .

Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

. К окружности, вписанной в треугольник , проведены три касательные. Периметры отсеченных треугольников равны , , . Найдите периметр данного треугольника.

Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника складывается из периметров отсеченных треугольников.

Ты нашел то, что искал? Поделись с друзьями!

Вот более сложная задача из вариантов ЕГЭ:

. Около окружности описан многоугольник, площадь которого равна . Его периметр равен . Найдите радиус этой окружности.

Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку — и проведите перпендикулярные сторонам радиусы в точки касания.

Соедините точку с вершинами . Получились треугольники и .
Очевидно, что площадь многоугольника .
Как вы думаете, чему равны высоты всех этих треугольников и как, пользуясь этим, найти радиус окружности?

🌟 Видео

Свойство касательной к окружности - ЧАСТЬ 1Скачать

Касательная к окружности. 8 классСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Касательная к окружностиСкачать