Поворот окружности на 180

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

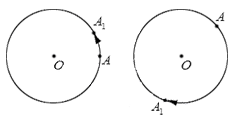
Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .

Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:

Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Полный оборот

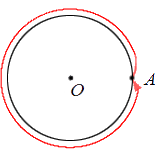
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .

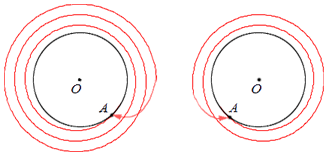
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .

Разберем характеристики угла поворота подробнее.

Видео:9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Направление поворота

Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

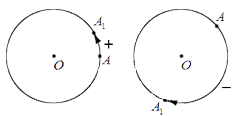
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.

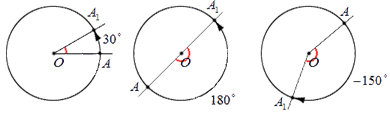
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :

Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

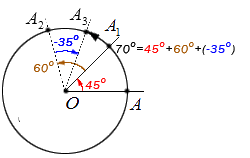
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:

Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .

По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .

Видео:9 класс, 33 урок, ПоворотСкачать

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

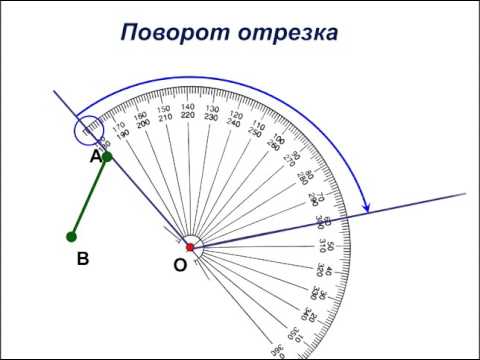
Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Дрифт на переднем приводе

После просмотра фильмов и роликов, где водители вытворяют необычные трюки со своими машинами, некоторые стараются повторять их. Сложные трюки, такие как езда на двух колесах на автомобиле, лучше даже не пытаться делать. Это требуем многих тренировочных занятий с мастерами каскадерами. А, что касается дрифта (sliding — скольжение), то его можно быстро научиться без наставника.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Что такое дрифт

Дрифт — это занос, которым можно управлять. Создается искусственно ради интереса или повышения уровня водительского мастерства. Для переднеприводных автомобилей другие правила выполнения дрифта. Дрифтовать на переднем приводе сложнее, поэтому не под силу с первого раза новичкам. Автомобиль ведет себя непредсказуемо во время заноса, поэтому надо научиться чувствовать движущую силу и силу инерции от тех или иных маневров.

Переднеприводные авто имеют большую устойчивость за счет того, что их передняя ось не только служит для управления транспортным средством, но и обеспечивает тягу машине. Классические марки и модели авто менее устойчивы на дорогах, поэтому и дрифтить на них легче.

Видео:§22 Поворот точки вокруг начала координатСкачать

Управляемый занос: теория

Передний дрифтинг делается так, чтобы задние колеса меньше контактировали с дорожным покрытием, а вес не передние колеса увеличивался. Удерживать при таких разных сцеплениях передних и задних колес с дорогой очень трудно. Для восстановления управляемости водитель использует руль и газ. Если баранка неудобна в заводском исполнении, то лучше сделать оплетку на руль для удобства и безопасности.

Новичка следует учиться в зимнее время года, когда на специальной площадке есть небольшой слой снега.

Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Техника дрифта

Кто умеет делать заносы на автомобиле на 180 или 360 градусов, они считаются профессионалами.

Разворот на 180 градусов

Считается, что разворот на пол оборота (180) можно сделать на любом переднеприводном автомобиле, в то время как разворот на полный оборот надо делать на подготовленных для таких трюков вождения автомобилях.

Если в конструкции автомобиля есть система стабилизации, то дрифт на 180 градусов не получится сделать.

Если стабилизирующую систему можно отключить, то дрифтовать надо только с отключенной системой.

Порядок разворота на 180 (способ №1):

1. Набрать скорость от 50 до 60 км/ч.
2. Полностью выжимают сцепление (на «классике» педаль сцепления не надо нажимать).
3. Резко повернуть руль в сторону задуманного разворота и, одновременно с вращением руля, поднять ручник с зажатой кнопкой.
4. Автомобиль разворачивается путем скольжения, после чего ручной тормоз следует опустить и остановить машину основным ножным тормозом.

Порядок разворота на 180 (способ №2):

1. На пониженной передаче машину завести в поворот не отпуская газ.
2. Во время поворота резко, но не до конца нажать тормозную педаль. Передние колодки при этом не успевают зажать диск, а задние колеса застопорились. Таким способом получается не сложны занос.

Порядок разворота на 180 (способ №3):

1. На скорости большей средней войти в поворот.
2. Скинуть педаль газа и тормозить двигателем. Машину в этом случае занесет, так как передок будет тормозить с направлением в сторону, а задняя часть приподнимется и ее понесет по инерции.

Разворот на 90 градусов

В отличие от дрифта на 180, на 90 выполнить сложнее. Потому что надо научиться вычислять угол во время поворота. От того, в какое время вы поднимите ручник, будет зависеть угол разворота.

Выполняется не сложно:

• разогнаться и, входя в поворот, поднять ручник;
• после того, как почувствовали, что машину развернуло почти на 90 градусов, отпустить ручной тормоз.

После того, как автомобиль развернуло, отпустили ручник, надо включить пониженную скорость и продолжить движение прямо.

Будьте готовы, что тренировка техники разворотов, дрифта, сожгут много топлива, времени, резины и уменьшит ресурс некоторых деталей конструкции автомобиля.

Лучше не делать дрифт на автомобилях с одноразовым двигателем. Да, да, есть моторы, которые не подлежат ремонту, например, это: различные модели Toyota с двигателями 3UZ-FE, 1AZ-FSE.

Разворот на 360 градусов

Такой разворот, на один оборот, мало кто делает на практике. Даже в фильмах чаще применяют развороты на 90 и 180 градусов. Для разворота на полный круг, требуется автомобиль с повышенной мощностью.

Порядок разворота на 360:

1. Разогнать машину до скорости от 80 до 90 км/ч.
2. Не отпуская педаль газа, нажать педаль сцепления.
3. Переключаем скорость на пониженную передачу с одновременным поворотом руля.
4. Поднять ручник с зажатой кнопкой (кнопку не отпускать).
5. После этого, автомобиль начнет разворачиваться и после того, как почувствуете, что автомобиль повернулся больше, чем на пол оборота, отпускаем ручник, отпускаем педаль сцепления и газуем. С помощью руля и сцепления доводим маневр до 360 градусов.

Видео:Радианная мера угла. 9 класс.Скачать

Разворот на асфальте

Без подготовки автомобиля с передним приводом можно начать проходить уроки по дрифту и разворотам зимой, когда покрытие скользкое. В случае, если участок дороги скользкий, то устанавливают знак Скользкая дорога в населенном пункте за 50-100 метров, вне населенного — за 150-300 метров.

Для летней тренировки требуется сначала подготовить машину:

• для лучшего сцепления с дорогой передние колеса (ведущие) устанавливают с широкой резиной;
• на задние колеса устанавливают узкие шины;
• настроить подвеску;
• отрегулировать трос ручного тормоза;
• настроить двигатель на максимальную мощность (если низкая компрессия в цилиндрах, сделать ремонт).

Совет: для того, чтобы уменьшить расходы на дрифты, на задние колеса следует установить «лысую» резину. Ее можно бесплатно набрать в шиномонтажках.

Видео:Центральная симметрия. 6 класс.Скачать

Техника разворота

С задней резиной без протекторов достаточно разогнаться до 60 км/ч, войти в поворот с ручником и автомобиль легко начнет мотать. Регулировка делается рулем и газом.

Правило заноса: поворачивать руль в ту сторону, в какую заносит автомобиль.

Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать

Видео

Дрифт на переднем приводе летом.

Дрифт на переднем приводе на автомобиле Lada Priora (Лада Приора).

Самый сложный финтр дрифта.

Как дрифтить на переднем приводе (ВАЗ 2114).

Видео:ПоворотСкачать

Угол поворота, угол произвольной величины.

В тригонометрии важным понятием является угол поворота. Ниже мы последовательно будем давать представление о повороте, и вводить все сопутствующие понятия. Начнем с общего представления о повороте, скажем о полном обороте. Далее перейдем к понятию угла поворота и рассмотрим его основные характеристики, такие как направление и величина поворота. Наконец, дадим определение поворота фигуры вокруг точки. Всю теорию по тексту будем снабжать поясняющими примерами и графическими иллюстрациями.

Навигация по странице.

Видео:ПоворотСкачать

Что называют поворотом точки вокруг точки?

Сразу отметим, что наряду с фразой «поворот вокруг точки» будем также использовать словосочетания «поворот около точки» и «поворот относительно точки», что обозначает одно и то же.

Введем понятие поворота точки вокруг точки.

Сначала дадим определение центра поворота.

Точку, относительно которой осуществляется поворот, называют центром поворота.

Теперь скажем, что получается в результате поворота точки.

В результате поворота некоторой точки A относительно центра поворота O получается точка A₁ (которая в случае некоторого количества полных оборотов может совпадать с A ), причем точка A₁ лежит на окружности с центром в точке O радиуса OA . Иными словами, при повороте относительно точки O точка A переходит в точку A₁ , лежащую на окружности с центром в точке O радиуса OA .

Считают, что точка O при повороте вокруг самой себя переходит в саму себя. То есть, в результате поворота вокруг центра поворота O точка O переходит в саму себя.

Также стоит отметить, что поворот точки А вокруг точки O стоит рассматривать как перемещение в результате движения точки А по окружности с центром в точке O радиуса OA .

Для наглядности приведем иллюстрации поворота точки А вокруг точки O , на рисунках, расположенных ниже, перемещение точки А в точку А₁ покажем при помощи стрелки.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Полный оборот

Можно выполнить такой поворот точки A относительно центра поворота O , что точка А , пройдя все точки окружности, окажется на прежнем месте. При этом говорят, что точка А совершила полный оборот вокруг точки O .

Дадим графическую иллюстрацию полного оборота.

Если же не останавливаться на одном обороте, а продолжать движение точки по окружности, то можно выполнить два, три и так далее полных оборотов. На чертеже ниже справа показано, как могут быть произведены два полных оборота, а слева — три оборота.

Можно также говорить о частях полного оборота, например, о половине оборота, трети, четверти и т.д. оборота (при надобности смотрите статью доли и обыкновенные дроби).

Видео:Фрезерный станок WEISAN XJ9512. В мою мастерскую более чем!Скачать

Понятие угла поворота

Из введенного в первом пункте понятия поворота точки понятно, что существует бесконечное множество вариантов поворота точки А вокруг точки O . Действительно, любую точку окружности с центром в точке O радиуса OA можно рассматривать как точку A₁ , полученную в результате поворота точки А . Поэтому, чтобы отличать один поворот от другого, вводится понятие угла поворота.

Одной из характеристик угла поворота является направление поворота. По направлению поворота судят о том, как осуществляется поворот точки – по часовой стрелке или против часовой стрелки.

Другой характеристикой угла поворота является его величина. Углы поворота измеряются в тех же единицах, что и углы в геометрии: наиболее распространены градусы и радианы. Здесь стоит заметить, что угол поворота может выражаться в градусах любым действительным числом из промежутка от минус бесконечности до плюс бесконечности, в отличие от угла в геометрии, величина которого в градусах положительна и не превосходит 180 .

Для обозначения углов поворота обычно используются строчные буквы греческого алфавита: и т.д. Для обозначения большого количества углов поворота часто применяют одну букву с нижними индексами, к примеру, .

Теперь поговорим о характеристиках угла поворота подробнее и по порядку.

Направление поворота

Пусть на окружности с центром в точке O отмечены точки A и A₁ . В точку А₁ можно попасть из точки A , выполнив поворот вокруг центра O либо по часовой стрелке, либо — против часовой стрелки. Эти повороты логично считать различными.

Условились считать поворотом в положительном направлении такой поворот, который осуществляется против хода часовой стрелки. Поворот по часовой стрелке называют поворотом в отрицательном направлении.

Проиллюстрируем повороты в положительном и отрицательном направлении. На чертеже ниже слева показан поворот в положительном направлении, а справа – в отрицательном.

Величина угла поворота, угол произвольной величины

Угол поворота точки, отличной от центра поворота, полностью определяется указанием его величины, с другой стороны, по величине угла поворота можно судить о том, как этот поворот был осуществлен.

Как мы уже упоминали выше, величина угла поворота в градусах выражается числом от −∞ до +∞ . При этом знак плюс соответствует повороту по часовой стрелке, а знак минус – повороту против часовой стрелки.

Теперь осталось установить соответствие между величиной угла поворота и тем, какому повороту она соответствует.

Начнем с угла поворота, равного нулю градусам. Этому углу поворота отвечает перемещение точки А в себя. Другими словами, при повороте на 0 градусов вокруг точки O точка А остается на месте.

Переходим к повороту точки А вокруг точки O , при котором поворот происходит в пределах половины оборота. Будем считать, что точка А переходит в точку А₁ . В этом случае абсолютная величина угла AOA₁ в градусах не превосходит 180 . Если поворот происходил в положительном направлении, то величина угла поворота считается равной величине угла AOA₁ , а если поворот происходил в отрицательном направлении, то его величина считается равной величине угла АОА₁ со знаком минус. Для примера приведем рисунок, показывающий углы поворота в 30 , 180 и −150 градусов.

Углы поворота большие 180 градусов и меньшие −180 градусов определяются на основе следующего достаточно очевидного свойства последовательных поворотов: несколько последовательных поворотов точки A вокруг центра O равносильны одному повороту, величина которого равна сумме величин этих поворотов.

Приведем пример, иллюстрирующий данное свойство. Выполним поворот точки А относительно точки O на 45 градусов, а затем еще повернем эту точку на 60 градусов, после чего повернем эту точку на −35 градусов. Обозначим промежуточные точки при этих поворотах как A₁ , A₂ и A₃ . В эту же точку А₃ мы могли попасть, выполнив один поворот точки A на угол 45+60+(−35)=70 градусов.

Итак, углы поворота, большие 180 градусов, мы будем представлять как несколько последовательных поворотов на углы, сумма величин которых дает величину исходного угла поворота. Например, угол поворота 279 градусов соответствует последовательным поворотам на 180 и 99 градусов, или на 90 , 90 , 90 и 9 градусов, или на 180 , 180 и −81 градус, или на 279 последовательных поворотов по 1 градусу.

Аналогично определяются и углы поворота, меньшие −180 градусов. К примеру, угол поворота −520 градусов можно интерпретировать как последовательные повороты точки на −180 , −180 и −160 градусов.

Подведем итог. Мы определили угол поворота, величина которого в градусах выражается некоторым действительным числом из промежутка от −∞ до +∞ . В тригонометрии мы будем работать именно с углами поворота, хотя слово «поворот» часто опускают, и говорят просто «угол». Таким образом, в тригонометрии мы будем работать с углами произвольной величины, под которыми будем понимать углы поворота.

В заключение этого пункта отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 градусов (или 2·π радианов), а в отрицательном – углу поворота в −360 градусов (или −2·π рад). При этом удобно большие углы поворота представлять как некоторое количество полных оборотов и еще один поворот на угол величиной от −180 до 180 градусов. Для примера возьмем угол поворота 1 340 градусов. Несложно 1 340 представить как 360·4+(−100) . То есть, исходному углу поворота отвечают 4 полных оборота в положительном направлении и последующий поворот на −100 градусов. Другой пример: угол поворота −745 градусов можно интерпретировать как два оборота против часовой стрелки и последующий поворот на −25 градусов, так как −745=(−360)·2+(−25) .

Видео:Тема: Движения. Урок: ПоворотСкачать

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко расширяется на поворот любой фигуры вокруг точки на угол (речь идет о таком повороте, что и точка, относительно которой осуществляется поворот, и фигура, которую поворачивают, лежат в одной плоскости).

Под поворотом фигуры будем понимать поворот всех точек фигуры вокруг заданной точки на данный угол.

В качестве примера приведем иллюстрацию следующему действию: выполним поворот отрезка AB на угол относительно точки O , это отрезок при повороте перейдет в отрезок A₁B₁ .

🔥 Видео

Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать