Постройте произвольный треугольник а1в1с1

Видео:№130. В треугольниках ABC и А1В1С1 отрезки СО и С1О1 — медианы, ВС=В1С1, ∠B = ∠B1 и ∠C=∠C1Скачать

И. Проверка домашнего задания

1) Что можно сказать про параллельную проекцию прямой на плоскость?

2) Что можно сказать о проекции параллельных прямых на плоскость?

3) Точка С делит отрезок АВ в отношении АС : СВ = 2 : 3. Параллельными проекциями точек А, В, С на плоскость а будут точки А1, B1, С1. В каком отношении точка С1 делит отрезок А1В1 ?

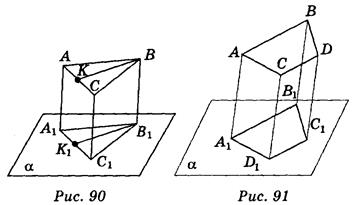
4) Треугольник А1В1С1 — параллельная проекция треугольника АВС на плоскость α (рис. 90). Укажите, какие из приведенных утверждений правильные, а какие — неправильные:

а) если треугольник АВС правильный, то треугольник А1В1С1 обязательно правильный;

б) треугольник АВС не может быть равен треугольнику А1В1С1;

в) если ВК — биссектриса треугольника АВС, то B1K1 обязательно — биссектриса треугольника А1В1С1;

г) если ВК — медиана треугольника АВС, то В1К1 обязательно — медиана треугольника A1B1C1.

5) Объясните решение задачи № 38.

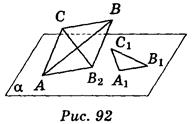
6) Четырехугольник A1B1C1D1 является параллельной проекцией рівнобічної трапеции ABCD (АВ — основание трапеции) на плоскость α (рис. 91). Укажите, какие из приведенных утверждений правильные, а какие — неправильные:

а) прямые A1D1 и В1С1 могут быть параллельными;

б) прямые A1B1 и D1C1 могут пересекаться;

в) отрезки А1 D 1 и В1С1 могут быть равными;

г) отрезки А1В1 и D1C1 могут быть равными;

д) если 2АВ = 3DC, то 3А1В1 = 2D1C1.

II. Закрепление и осмысление знаний учащихся

Формирование умений строить изображения фигур

Остановимся на изображении наиболее применяемых геометрических фигур, из комбинаций которых состоит, как правило, изображения любой сложной пространственной фигуры.

Любой треугольник может быть изображением треугольника произвольной формы, в частности: правильного, равнобедренного, прямоугольного.

Доведение

Пусть задан треугольник АВС произвольной формы и на плоскости проекции α задан треугольник А1В1С1. Всегда можно расположить треугольник АВС и выбрать направление проектирования так, что треугольник проецируется в треугольник, подобный треугольнику А1В1С1 (рис. 92). Построим треугольник AB2C, который подобен треугольнику А1В1С1 выбрав за направление проектирования прямую BB2, получим, что ΔАВС проектируется в ΔАВ2С такой, что ΔАВС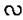ΔА1В1С1.

Следует отметить, что медианы и средние линии треугольника изображают соответственно медіанами и средними линиями изображения.

На изображении равностороннего треугольника постройте изображение его центра.

Решение

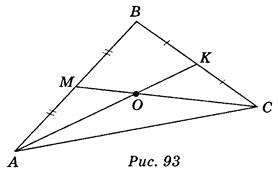
Пусть АВС (рис. 93) — данное изображение равностороннего треугольника. Центр правильного треугольника — точка пересечения его медиан. Поэтому, построив медианы АК и CM на изображении, которые пересекутся в точке О, получим: точка О — центр правильного треугольника АВС.

ИЗОБРАЖЕНИЕ ПАРАЛЛЕЛОГРАММА

Изображением параллелограмма (прямоугольника, ромба, квадрата) можно считать произвольный параллелограмм, принадлежащей плоскости проекций.

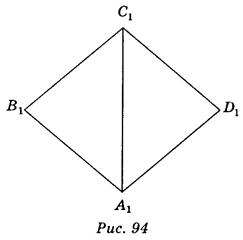
Действительно, пусть ABCD — параллелограмм, что проектируют, тогда произвольный треугольник А1В1С1 можно считать проекцией треугольника АВС (рис. 94). Учитывая, что при параллельном проектировании параллельные отрезки переходят в параллельные отрезки, и проведя A1 D 1 || В1С1 и C 1 D 1 || А1В1, получим A1B1C1D1 — параллелограмм, который является изображением параллелограмма ABCD (в частности, прямоугольника, ромба, квадрата).

Постройте изображение ромба с углом 120° и изображение высоты ромба, проведенная из вершины этого угла.

Решение

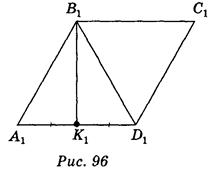
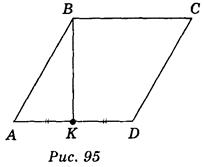
Пусть параллелограмм ABCD (рис. 95) является изображением ромба A 1 B 1 C 1 D 1 , у которого B 1 = 120° (рис. 96).

Поскольку Δ А1В1 D 1 — равносторонний, то его медиана В1 K 1 является одновременно и высотой этого треугольника, а следовательно, и ромба.

Таким образом, построив середину стороны AD и соединив эту точку с вершиной В, получим ВК — изображение высоты (см. рис. 95).

ИЗОБРАЖЕНИЕ ТРАПЕЦИИ

Из свойства параллельного проектирования следует, что изображением трапеции есть трапеция, у которой отношение длин оснований изображения равно отношению длин оснований трапеции, которую проектируют.

Постройте изображение рівнобічної трапеции с основаниями 3 и 9 см и изображения ее высоты.

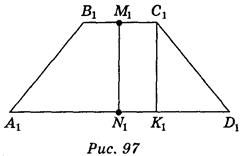
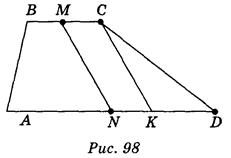
Пусть A1B1C1D1 — равносторонняя трапеция, у которой А1 D 1 || В1С1, A1D1 = 9 см, В1С1 = 3 см. Следует отметить, что высота С1К1 параллельна оси симметрии М1 N 1 (точки М1 и N1 — середины оснований трапеции) (рис. 97). Но при параллельном проецировании сохраняются параллельность прямых и отношение длин параллельных отрезков. Отсюда вытекает построение: трапеция ABCD, в которой AD || ВС и AD = 3 ВС, является изображением трапеции (рис. 98); построив точки М и N — середины сторон ВС и AD и СК || MN, получим отрезок СК — изображение высоты трапеции.

ИЗОБРАЖЕНИЕ ЧЕТЫРЕХУГОЛЬНИКА

Изображением произвольного четырехугольника (параллелограмма и трапеции) есть произвольный четырехугольник.

ИЗОБРАЖЕНИЕ ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА

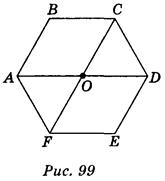
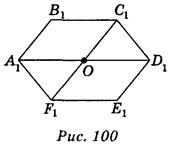
Рассмотрим правильный шестиугольник ABCDEF (рис. 99). Точка О пересечения диагоналей AD и FC — его центр симметрии, поэтому ромба АВСО и DEFO симметричны относительно точки О. Ромб АВСО изображаем в виде произвольного параллелограмма A1B1C1 D 1 (рис. 100). Для построения последних вершин изображение достаточно построить точки D 1, E 1, F 1, соответственно симметричны относительно точки О1 точкам А1, B1, С1.

ИЗОБРАЖЕНИЕ КРУГА

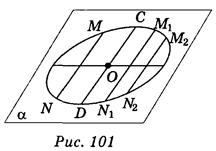
Изображением круга с центром в точке О1 является эллипс с центром в точке О, который принадлежит плоскости проекции α . Каждый диаметр эллипса АВ делит пополам хорды MN, M1N1, M2N2 . параллельные сопряженного с ним диаметра CD (рис. 101).

Следует отметить, что сопряженными диаметрами эллипса называются изображения двух перпендикулярных диаметров круга, что проецируется.

Решение задачи № 42 из учебника (с. 22).

ИЗОБРАЖЕНИЕ ТЕТРАЭДРА

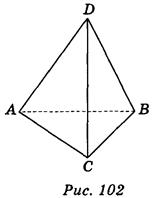
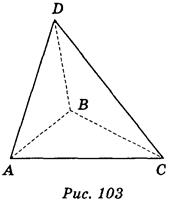
Рассматривая тень, что дают на экране каркасная модель тетраэдра, можно сформулировать правило его изображение. Изображением ребер данного тетраэдра могут быть стороны и диагонали произвольного выпуклого (рис. 102) или невыпуклого четырехугольника ABCD (рис. 103).

ИЗОБРАЖЕНИЕ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА

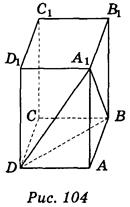
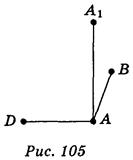
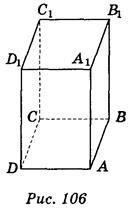
Пусть задан прямоугольный параллелепипед ABCDA1 B 1C1D1. Выберем три его ребра АВ, AD и АА1, имеющих общее начало (рис. 104). Рассмотрим тетраэдр A1ABD. Пользуясь правилом изображения тетраэдра, приходим к выводу, что ребра АВ, AD, AA1 можно изобразить в виде трех произвольных отрезков, выходящих из одной точки (рис. 105). Последние его ребра следует изобразить определенными отрезками, каждый из них параллельный одном из построенных отрезков и равен ему по длине (рис. 106).

III. Домашнее задание

§2, п. 13; контрольный вопрос № 12; задачи № 39, 40 (с. 22).

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

IV. Подведение итога урока

Вопрос к классу

1. Четырехугольник A1B1C1 D 1 является параллельной проекцией трапеции ABCD (AD — основание трапеции) на некоторую плоскость. Укажите, какие из указанных утверждений правильные, а какие — неправильные:

а) четырехугольник A1 B 1 C 1 D 1 является трапецией с основанием C1D1;

б) четырехугольник А1В1 C 1 D 1 может быть ромбом;

в) четырехугольник A1B1C1D1 является трапецией с основанием А1 D 1;

г) четырехугольник A1B1C1D1 является трапецией с основанием В1 D 1;

д) если ВС = 5AD, то 5В1 C 1 = A1 D 1.

2. Четырехугольник A1B1C1D1 является параллельной проекцией прямоугольника ABCD на некоторую плоскость. Укажите, какие из перечисленных утверждений являются правильными, а какие — неправильными:

а) в четырехугольнике A1B1 C 1 D 1 является параллельные стороны;

б) в четырехугольнике А1 B 1С1 D 1 обязательно есть равные стороны;

в) четырехугольник A1 B 1С1 D 1 может быть трапецией;

г) диагонали четырехугольника A1B1C1D1 точкой пересечения делятся пополам;

д) диагонали четырехугольника А1 B 1С1 D 1 уровне обязательно.

Видео:ГЕОМЕТРИЯ С НУЛЯ. УРОК-5. ПРОИЗВОЛЬНЫЙ ТРЕУГОЛЬНИКСкачать

Дан равносторонний треугольник ABC. С помощью циркуля и линейки постройте равносторонний треугольник А1В1С1 так, что А1 ϵ ВС, В1 ϵ АС, С1 ϵ АВ

Видео:Построение высоты в треугольникеСкачать

Ваш ответ

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

решение вопроса

Видео:№161. В треугольниках ABC и А1B1С1 медианы AM и А1М1 равны, BC=B1С1 и ∠AMB=∠A1M1B1. Докажите, чтоСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,006
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Построение медианы в треугольникеСкачать

Начертите произвольный треугольник ABC и выберите внутри его произвольную точку А1, постройте треугольник А1В1С1 = треугольнику АВС так, чтобы его стороны были параллельны сторонам треугольника АВС?

Геометрия | 5 — 9 классы

Начертите произвольный треугольник ABC и выберите внутри его произвольную точку А1, постройте треугольник А1В1С1 = треугольнику АВС так, чтобы его стороны были параллельны сторонам треугольника АВС.

60 градусов, следует из свойств, что поворот сохраняет расстояние между точками и переводит отрезки в отрезки, лучи в лучи, прямые в прямые.

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Начертите треугольник авс измерьте стороны с помощью линейки?

Начертите треугольник авс измерьте стороны с помощью линейки.

Видео:Построить описанную окружность (Задача 1)Скачать

Точка М лежит на стороне ВС треугольника АВС, точка К на стороне АС?

Точка М лежит на стороне ВС треугольника АВС, точка К на стороне АС.

Известно, что треугольник АВМ равен треугольнику ВСК.

Что можно сказать о треугольнике АВС?

Видео:№262 В треугольниках ABC и А1В1С1 углы А и А1 — прямые, BD и В1D1— биссектрисы. Докажите, чтоСкачать

Треугольники АВС и КВМ подобны, стороны треугольника КВМ в 4 раза больше сторон треугольника АВС?

Треугольники АВС и КВМ подобны, стороны треугольника КВМ в 4 раза больше сторон треугольника АВС.

Площадь треугольника АВС равна 8.

Найдите площадь треугольника КВМ.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Начертите произвольный треугольник ABC ?

Начертите произвольный треугольник ABC .

Постройте медиану CM.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Начертите произвольный остроугольный треугольник ABC и постройте точку пересечения высоты BD и биссектрисы AL этого треугольника?

Начертите произвольный остроугольный треугольник ABC и постройте точку пересечения высоты BD и биссектрисы AL этого треугольника.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Точка Т лежит на стороне АВ треугольника АВС, а точка Д — середина стороны ВС?

Точка Т лежит на стороне АВ треугольника АВС, а точка Д — середина стороны ВС.

Известно что ВТ = 8см , ВС = 12см, угол ВТД = углу АВС и треугольник ТВД подобен треугольнику СВА.

Вычислите длину стороны АВ треугольника АВС.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Прямая, параллейная стороне АС треугольника АВС, пересекает сторону АВ в точке А1, а сторону ВС — в точке С1?

Прямая, параллейная стороне АС треугольника АВС, пересекает сторону АВ в точке А1, а сторону ВС — в точке С1.

Докажите, что углы треугольника АВС равны углам треугольника А1ВС1.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

В треугольнике АВС точки А1В1С1 середины сторон ?

В треугольнике АВС точки А1В1С1 середины сторон .

Равс = 45см , найти стороны треугольника АВС.

Видео:Задача 1.1. Прямая и плоскость. Построить комплексный чертеж треугольника АВС и прямой МN.Скачать

Начертите произвольный треугольник ABC?

Начертите произвольный треугольник ABC.

Постройте прямую AM, параллельную прямой BC.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

1) Начертите остроугольный треугольник АВС?

1) Начертите остроугольный треугольник АВС.

Проведите из его вершины А медиану, биссектрису и высоту.

2) Постройте произвольный треугольник.

Проведите его медиану и высоту.

Помогите пожалуйста очень срочно!

Вы зашли на страницу вопроса Начертите произвольный треугольник ABC и выберите внутри его произвольную точку А1, постройте треугольник А1В1С1 = треугольнику АВС так, чтобы его стороны были параллельны сторонам треугольника АВС?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Треугольник не только прямоугольный , но и с равными катетами, равнобедренный, значит углы при основании 45тангенс 45 = 1.

Катет против угла в 30 градусов равен половине гипотенузы. Этот же катет прилежит к углу в 60 градусов. Гипотенуза т. О. будет 4 * 2 = 8.

По теореме синусов : x / sin(30°) = 12 / sin(90°) = > = >x / sin(30°) = 12 = > = >x = 12 * sin(30°) = > = >x = 12 * 0, 5 = > = >x = 6 (см) ; Ответ : 6 см.

Сумма угла 1 и 2 180 градусов. Угол 2 равен 180 — 125 = 55 градусов. Сумма всех углов 1, 2, 3 и 4 равна 360 градусов. Углы 1 и 3 одинаковые, значит угол 3 равен 125 градусов. Угол 4 — это или 360 — 125 — 125 — 55 = 55 градусов, или аналогично с у..

В результате обмена веществ организм получает энергию для своих жизненных процессов (энергетический обмен) и материал для построения и обновления клеток. (пластические процессы).

Решение задания приложено с поправкой.

Только одно верное утверждение : любые два равносторонние треугольники подобны. Так как все 3 угла равностороннего треугольника равны 60 градусов, а если у двух треугольников два угла равны, то такие треугольники подобны.

150 : 5 = 30 30 * 9, 5 = 285 руб.

150 / 5 * 9, 5 = 285 рублей.

В)АС = СВ этот треугольник прямоугольный треугольник , потому что там угол С = 90° сумма всех сторон треугольника = 180° 180° — (90° + 45°) = 45° — это значит , что АС = СВ АС и СВ являются катетами.

🌟 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать