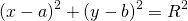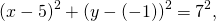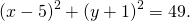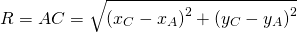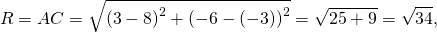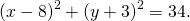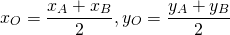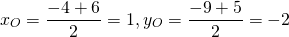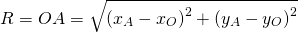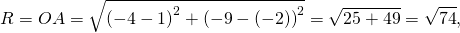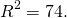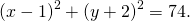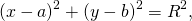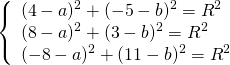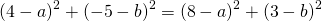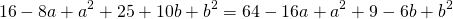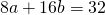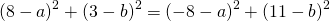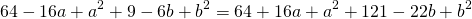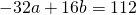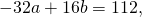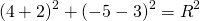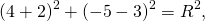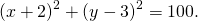Построение криволинейных объектов
Команда ARC, формирующая дугу, вызывается из падающего меню Draw > Arc или щелчком на пиктограмме Arc на панели инструментов Draw (рис. 8.1).
Дуги можно строить различными способами. По умолчанию построение производится путем указания трех точек: начальной, промежуточной и конечной. Дугу можно также определить, задав центральный угол, радиус, направление или длину хорды. По умолчанию дуга рисуется против часовой стрелки.
Запросы команды ARC:
Specify start point of arc or [Center]: – указать начальную точку дуги
Specify second point of arc or [Center/End]: – указать вторую точку дуги
Specify end point of arc: – указать конечную точку дуги
Ключи команды ARC:
? Center – точка центра дуги;
? End – конечная точка дуги;
? Angle – величина угла;
? chord Length – длина хорды;
? Direction – направление касательной;
? Radius – радиус дуги.
Рис. 8.1. Команда построения дуги в падающем меню
Существует несколько способов построения дуги при помощи команды ARC:
? 3 Points – построение дуги по трем точкам, лежащим на дуге;
? Start, Center, End – построение дуги по стартовой точке, центру и конечной точке дуги;
? Start, Center, Angle – построение дуги по стартовой точке, центру и углу;
? Start, Center, Length – построение дуги по стартовой точке, центру и длине хорды;
? Start, End, Angle – построение дуги по стартовой точке, конечной точке и углу;
? Start, End, Direction – построение дуги по стартовой точке, конечной точке и направлению – углу наклона касательной из начальной точки;
? Start, End, Radius – построение дуги по стартовой точке, конечной точке и радиусу;
? Center, Start, End – построение дуги по центру, стартовой и конечной точке;
? Center, Start, Angle – построение дуги по центру, стартовой точке и углу;
? Center, Start, Length – построение дуги по центру, стартовой точке и длине хорды;
? Continue – построение дуги как продолжения предшествующей линии или дуги.
Пример. Построение дуги по трем точкам
Постройте дугу по варианту 3 Points – рис. 8.2.
Запустите команду ARC, вызвав ее из падающего меню Draw > Arc > 3 Points или щелкнув на пиктограмме Arc на панели инструментов Draw. Ответьте на запросы:
Specify start point of arc or [Center]: 50,80 – точка 1
Specify second point of arc or [Center/End]: 50,20 – точка 2
Specify end point of arc: 20,50 – точка 3
Рис. 8.2. Построение дуги по трем точкам
Команда CIRCLE, формирующая окружность, вызывается из падающего меню Draw > Circle или щелчком на пиктограмме Circle на панели инструментов Draw (рис. 8.3).
Окружности можно строить различными способами. По умолчанию построение производится путем указания центра и радиуса. Можно задавать центр и диаметр или только диаметр, указывая его начальную и конечную точки. Окружность также может строиться по трем точкам. Кроме того, имеется возможность определять окружность, касающуюся либо трех объектов рисунка, либо двух (в последнем случае задается еще и радиус).
Запросы команды CIRCLE:
Specify center point for circle or [3P/2P/Ttr (tan tan radius)]: – указать центр окружности
Specify radius of circle or [Diameter]: – указать радиус
Рис. 8.3. Команда построения окружности в падающем меню
Ключи команды CIRCLE:
? 3Р – строит окружность по трем точкам, лежащим на окружности;
? 2P – строит окружность по двум точкам, лежащим на диаметре;
? Ttr – строит окружность по двум касательным и радиусу.
Пример. Построение окружности по центру и радиусу
Постройте окружность по центру и радиусу (рис. 8.4).
Запустите команду CIRCLE, вызвав ее из падающего меню Draw > Circle > Center, Radius или щелкнув на пиктограмме Circle на панели инструментов Draw. Ответьте на запросы:
Specify center point for circle or [3P/2P/Ttr (tan tan radius)]: 50,50 – точка центра окружности
Specify radius of circle or [Diameter] : 30 – радиус окружности
Рис. 8.4. Построение окружности по центру и радиусу
Пример. Построение окружности по двум точкам диаметра
Постройте окружность по двум точкам диаметра (рис. 8.5).
Запустите команду CIRCLE, вызвав ее из падающего меню Draw > Circle > 2 Points или щелкнув на пиктограмме Circle на панели инструментов Draw. Ответьте на запросы:
Specify center point for circle or [3P/2P/Ttr (tan tan radius)]: 2P – переход в режим построения окружности по двум точкам
Specify first end point of circle’s diameter: 50,80 – точка 1
Specify second end point of circle’s diameter: 50,20 – точка 2
Рис. 8.5. Построение окружности по двум точкам диаметра
Команда SPLINE, формирующая сплайн, вызывается из падающего меню Draw > Spline или щелчком на пиктограмме Spline на панели инструментов Draw.
Сплайн представляет собой гладкую кривую, проходящую через заданный набор точек. Сплайны применяются для рисования кривых произвольной формы, например горизонталей в географических информационных системах или при проектировании автомобилей.
Запросы команды SPLINE:
Specify first point or [Object]: – указать первую точку Specify next point: – указать следующую точку
Specify next point or [Close/Fit tolerance] : – указать следующую точку
Specify next point or [Close/Fit tolerance] : – указать следующую точку
Specify next point or [Close/Fit tolerance] : – нажать клавишу Enter
Specify start tangent: – указать касательную в начальной точке Specify end tangent: – указать касательную в конечной точке Ключи команды SPLINE:
? Object – преобразование полилинии в сплайн;
? Close – замкнуть сплайн;
? Fit tolerance – определение допуска – максимально допустимого расстояния от реального сплайна до любой из определяющих точек.
Команда ELLIPSE, обеспечивающая формирование эллипса, вызывается из падающего меню Draw > Ellipse или щелчком на пиктограмме Ellipse на панели инструментов Draw (рис. 8.6).
Рис. 8.6. Команда построения эллипса в падающем меню
По умолчанию построение эллипсов производится путем указания начальной и конечной точек первой оси, а также половины длины второй оси. Самая длинная ось эллипса называется его большой осью, самая короткая – малой.
Запросы команды ELLIPSE:
Specify axis endpoint of ellipse or [Arc/Center]: – указать конечную точку оси эллипса
Specify other endpoint of axis: – указать вторую конечную точку оси эллипса
Specify distance to other axis or [Rotation]: – указать длину другой оси
Ключи команды ELLIPSE:
? Arc – режим построения эллиптических дуг;
? Center – указание центра эллипса;
? Rotation – режим построения эллипса указанием поворота относительно главной оси.
Пример. Построение эллипса по двум осям
Постройте эллипс по конечным точкам первой оси и половине длины второй оси (рис. 8.7).
Запустите команду ELLIPSE, вызвав ее из падающего меню Draw > Ellipse или щелкнув на пиктограмме Ellipse на панели инструментов Draw. Ответьте на запросы:
Specify axis endpoint of ellipse or [Arc/Center]: 10,20 – начало первой оси эллипса
Specify other endpoint of axis: 80,80 – конечная точка первой оси эллипса
Specify distance to other axis or [Rotation]: 20 – половина длины второй оси эллипса
Рис. 8.7. Построение эллипса
Команда REVCLOUD предназначена для формирования облака, вызывается из падающего меню Draw > Revision Cloud или щелчком на пиктограмме Revision Cloud на панели инструментов Draw.
Геометрический объект «облако», использующийся для нанесения различных пояснительных надписей и пометок к элементам чертежа, представляет собой полилинию с дуговыми сегментами (рис. 8.8).
Запросы команды REVCLOUD:
Minimum arc length: 15 Maximum arc length: 15 Style: Normal – значения максимальной и минимальной длин дуги и установленный стиль
Specify start point or [Arc length/Object/Style] : – указать начальную точку или ввести ключ
Guide crosshairs along cloud path. – провести курсор по контуру облака
Revision cloud finished. – облако построено
Рис. 8.8. Построение облака
Ключи команды REVCLOUD:
? Arc length – режим указания значения максимальной и минимальной длин дуги;
? Object – преобразование объекта в облако;
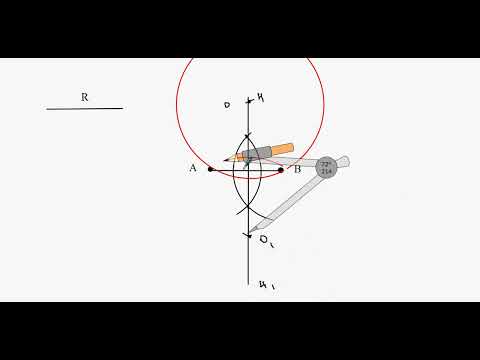
- Пустая окружность по двум точкам
- Уравнение окружности по двум точкам и радиусу
- Как строить окружность по точкам
- Окружность
- Основные характеристики окружности
- Построение окружности
- Уравнение с двумя переменными и его график. Уравнение окружности
- п.1. Понятие уравнения с двумя переменными
- п.2. Обобщенные правила преобразования графика уравнения
- п.4. Примеры
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Всё про окружность и круг
- Уроки по программе AutoCAD.
- Урок №7 Построение окружности в AutoCAD.
- Список последних уроков по программе AutoCAD.
- 🌟 Видео
Видео:Построение окружности по трём точкам.Скачать

Пустая окружность по двум точкам
Видео:Построение окружности по трем точкамСкачать

Уравнение окружности по двум точкам и радиусу
| Главная | Шутки | Форум |
 |
| План занятий |
 |





Окружность. Центр окружности. Радиус окружности.
Уравнение окружности. Уравнение касательной к окружности.
Условие касания прямой и окружности.
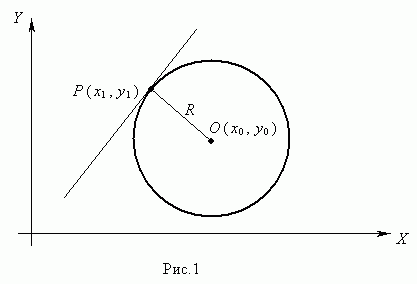
Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.
Уравнение окружности радиуса R с центром в точке О ( х , у ) имеет вид:
Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:
Пусть Р ( х 1 , у 1 ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
Следовательно, уравнение данной окружности
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
Таким образом, уравнение окружности с диаметром AB —
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
получаем систему уравнений:
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
Приравняем правые части 2-го и 3-го уравнений:
на -1 и сложив результат почленно с уравнением
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
Следовательно, уравнение окружности, проходящей через три данные точки —
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
Для расчета уравнения, надо знать определение окружности. Итак, окружность – это множество точек в пространстве, равноудаленных от одной точки, называемой центром. Отрезок, соединяющий две точки окружности и проходящий через точку центра, называется диаметром. Отрезок, соединяющий две точки окружности – хорда. Отрезок, соединяющий центр и любую точку окружности – радиус. Радиус равен половине диаметра.
Рассчитывая уравнение окружности, получаем следующие данные:
• координаты точки центра;
• длину радиуса.
И наоборот, зная длину радиуса и координаты точки центра, можно определить координаты любой точки и начертить окружность.
Для чего необходимо рассчитывать уравнение окружности? Зная длину радиуса, который рассчитывается, исходя из данных уравнения, можно определить длину любой окружности и площадь круга по следующим формулам:
• l=2πr, где l – длина окружности, π=3,14
• S=πr2
Следует помнить, круг – это множество точек на плоскости координат, расположенных внутри окружности. Оптимальный способ рассчитать уравнение окружности – воспользоваться онлайн калькулятором. Это ускорит процесс и позволит быстро решить задачи по соответствующим формулам.
Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Как строить окружность по точкам
Видео:1 2 4 сопряжение окружностейСкачать

Окружность
Окружность — это замкнутая кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Заданная точка является центром окружности. На Рис.1 точка О — центр окружности.
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Основные характеристики окружности
1. Радиус — это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.
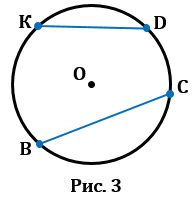
2. Хорда — это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD — хорды окружности с центром в точке О.
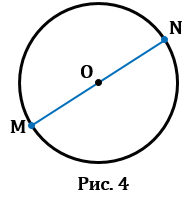
3. Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр — это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN — диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.
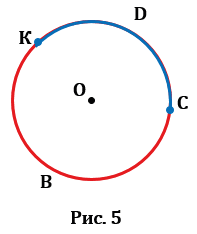
4. Дуга — это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC — дуги, ограниченные точками К и С.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Построение окружности
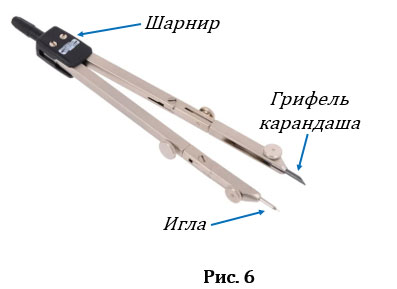
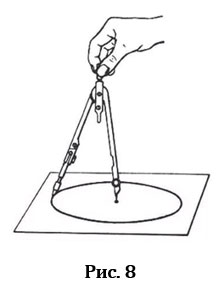
Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.
Выполнение построения:
- отмечаем точку, которая будет центром окружности;
- делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);
- ставим иглу циркуля в точку, которая определяет центр окружности;
- проводим окружность данного радиуса (Рис.8).
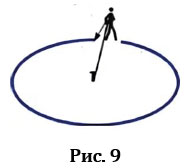
Для того, чтобы построить окружность на местности используют веревку. Сначала отмечаем место, которое будет определять центр окружности, вбиваем в это место колышек, привязываем к нему один конец веревки и отходим, держа другой конец веревки на расстояние равное радиусу окружности, которую мы хотим получить, отмечаем линию окружности (Рис.9).
Часть плоскости, которая ограничена окружностью (выделена черным цветом), называется кругом (выделен голубым цветом) (Рис.10).
Поделись с друзьями в социальных сетях:
Видео:Построение внешней касательной к двум дугам окружностей. Урок11.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm ) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm ) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm =-frac + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm > ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm =2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm > ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm =-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm +2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Видео:Уравнение окружности (1)Скачать

Please wait.
Видео:Построение внутренней касательной к двум дугам окружностей.Урок12.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

We are checking your browser. mathvox.ru
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:КОМПАС 3D - [Окружность по двум точкам]Скачать
![КОМПАС 3D - [Окружность по двум точкам]](https://i.ytimg.com/vi/vYad8HSnNQA/0.jpg)
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6cef2f4bcbea1616 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Видео:Длина окружности. Математика 6 класс.Скачать

Уроки по программе AutoCAD.
Урок №7 Построение окружности в AutoCAD.
Окружность в AutoCAD можно построить несколькими способами:
- По центральной точке и радиусу;
- По центральной точке и диаметру;
- По двум конечным точкам диаметра;
- По трем точкам;
- С заданным радиусом касательно к двум объектам;
- Касательную к трем объектам.
Мы рассмотрим каждый из этих способов.
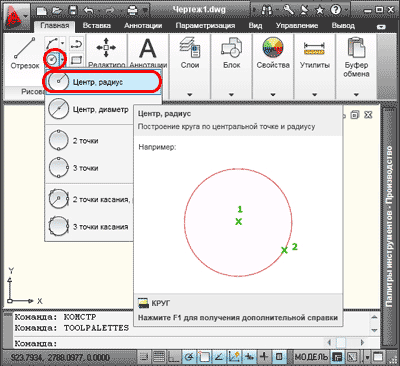
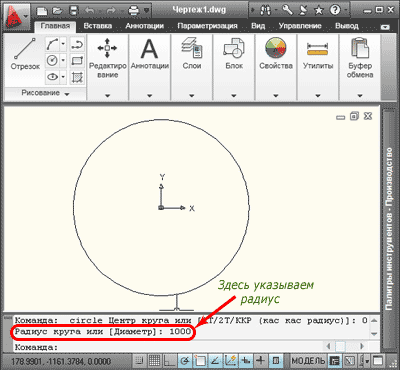
1. Чтобы построить окружность по центральной точке и заданному радиусу, на вкладке «Главная» в панели «Рисование» открываем раскрывающийся список «Круг», из списка выбираем команду «Центр, радиус», или в командной строке набираем команду (_circle), нажимаем «Enter».
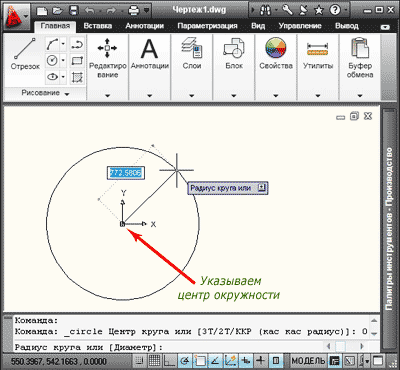
Программа попросит указать центр окружности. Это можно сделать при помощи курсора, или указав координаты в командной строке. Укажем точку с координатами (0,0), нажимаем клавишу «Enter».
Теперь нужно указать радиус (к примеру, 1000), нажимаем клавишу «Enter», окружность построена. Разумеется, радиус можно задавать при помощи курсора и мышки.
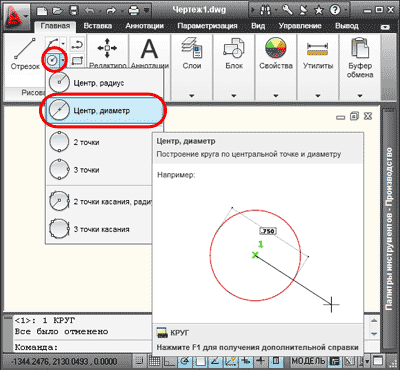
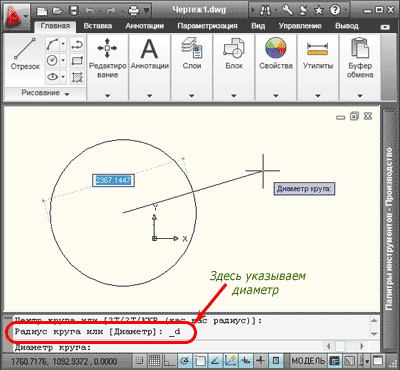
2. Вы уже наверно догадались, что построение окружности по центральной точке и диаметру выполняются аналогично. Из раскрывающегося списка «Круг» нужно выбрать команду «Центр, диаметр». Через командную строку последовательно набираются команды (_circle), нажимаем «Enter», после указания центра набираем (_d) нажимаем «Enter».
Дальнейшие построения подобны описанным выше, с той лишь разницей, что вместо радиуса задаем диаметр.
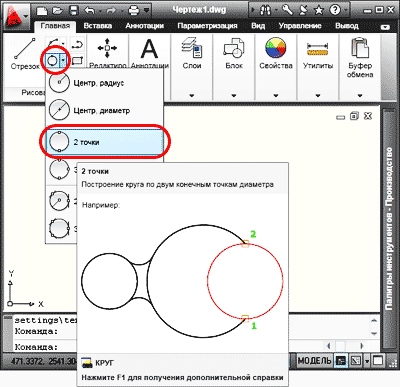
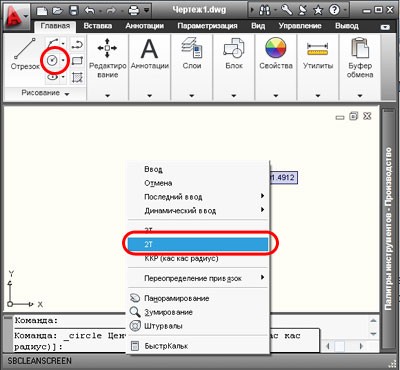
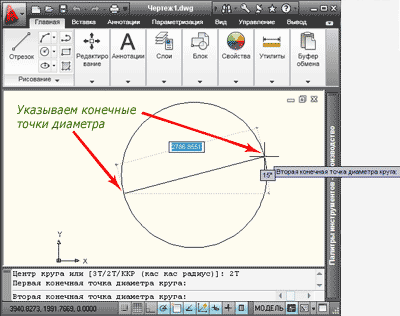
3. Для построения окружности по двум конечным точкам диаметра, из выпадающего списка «Круг» выбираем команду «2 точки».
Либо можно после нажатия кнопки «Круг» вызвать контекстное меню и из выпадающего списка выбрать команду «2Т» (для англоязычных версий программы «2Р»).
Теперь последовательно задаем первую конечную точку диаметра и вторую конечную точку. Точки можно вводить в командную строку или указывать при помощи курсора и мыши. Если Вы работаете с командной строкой, то вводится команда (_circle), нажимаем «Enter», теперь набираем команду (2Т). Обратите внимание в приведенном примере, для русскоязычной версии программы, при вводе команды (2Т) – раскладка клавиатуры Русская. Теперь задаем конечные точки диаметра.
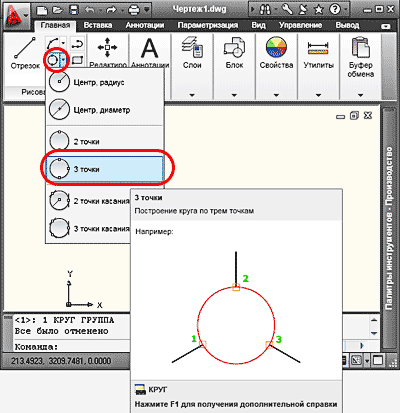
4. Построение окружности по трем принадлежащим ей точкам, выполняется аналогично предыдущему способу, только указываем три точки принадлежащие этой окружности.
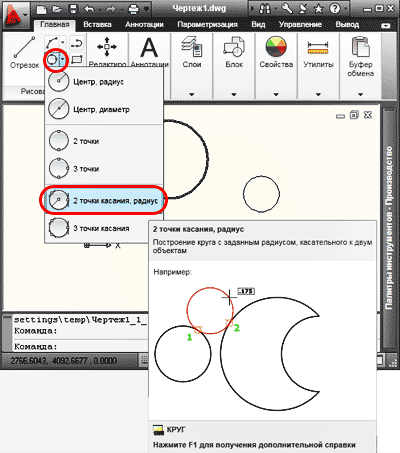
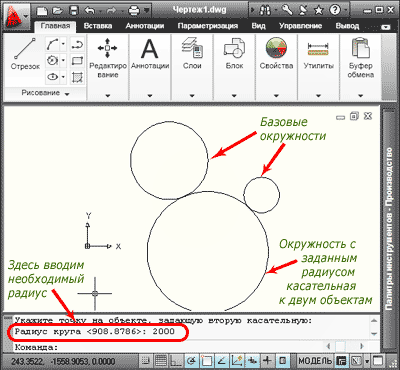
5. Чтобы рассмотреть построение окружности с заданным радиусом, касательно к двум объектам, предварительно построим две окружности. Из раскрывающегося списка «Круг» выбираем команду «2 точки касания, радиус».
Указываем курсором первый объект для построения касательной, затем второй объект. В командной строке вводим необходимый радиус (например 2000), нажимаем «Enter». Окружность с заданным радиусом касательная к двум объектам построена.
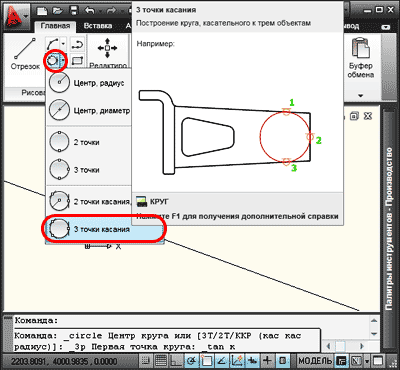
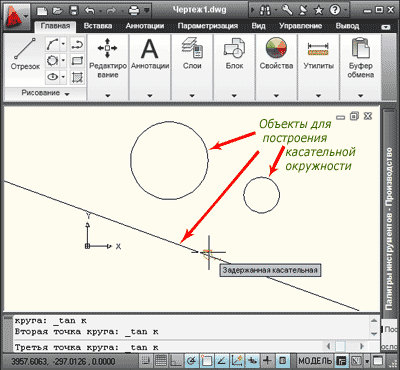
6. Для построения окружности касательной к трем объектам, из раскрывающегося списка «Круг» выбирается команда «3 точки касания».
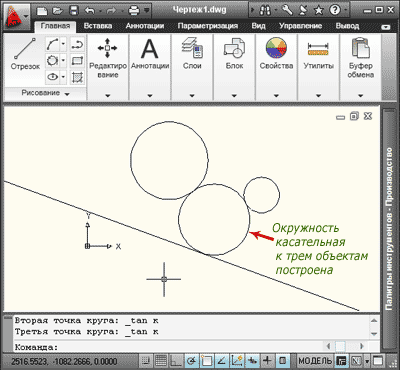
Указываем курсором объекты для построения касательной окружности.
Окружность касательная к трем объектам построена.
В следующем уроке, поговорим о построении эллипсов.
Если у Вас есть вопросы можно задать их ЗДЕСЬ.
Список последних уроков по программе AutoCAD.
Автор: Дмитрий Родин
«AutoCAD ЭКСПЕРТ»
Видео самоучитель По AutoCAD
- 60 наглядных видеоуроков;
- Более 15 часов только AutoCAD;
- Создание проектов с нуля прямо у Вас на глазах;
- 365-дневная гарантия
>> Читать Полное Описание
 Автор: Саляхутдинов Роман«БОСК 5.0» Новый Видеокурс. «Твердотельное и Поверхностное Моделирование в КОМПАС-3D»
>> Читать Полное Описание
|