Построение треугольника практические задания

Разделы: Математика

Класс: 7

Цели урока:

максимально донести до учащихся изучаемый материал;
• развивать мышление, память, умение свободно пользоваться циркулем;
• попытаться повысить активность и самостоятельность учащихся при выполнении заданий.

Оборудование:

школьный циркуль
• транспортир,
• линейка,
• карточки для самостоятельной работы.

Тема урока: «Задачи на построение».

Сегодня мы будем учиться строить треугольники по трем заданным элементам с помощью циркуля и линейки.

Чтобы построить треугольник, нужно сначала уметь строить отрезок, равный заданному, и угол, равный заданному. Конечно, можно это сделать с помощью линейки с делениями и транспортира, но в математике требуется еще и уметь выполнять построения с помощью циркуля и линейки без делений.

Любая задача на построение включает в себя четыре основных этапа:

• анализ;
• построение;
• доказательство;
• исследование.

Анализ и исследование задачи необходимы так же, как и само построение. Необходимо посмотреть, в каких случаях задача имеет решение, а в каких – решения нет.

1. Построение отрезка, равного заданному.

2. Строим угол, равный заданному, с помощью циркуля и линейки.

А вот теперь перейдем к построению треугольников по трем элементам.

3. Построение треугольника по двум сторонам и углу между ними.

Дано	Требуется построить	Построение
1. Построить угол А, равный заданному углу. 2. На одной стороне угла отметить точку С так, чтобы отрезок АС был равен заданному отрезку b. 3. На другой стороне угла отметить точку В так, чтобы отрезок АВ был равен заданному отрезку с. 4. Соединить с помощью линейки точки В и С.

Построен треугольник АСВ по двум сторонам и углу между ними.

Самостоятельная работа к схеме 3.

Построить треугольник ВСН, если ВС = 3 см, СН = 4 см, С = 35є.

Построить треугольник СДЕ, у которого ДС = 4 см, ДЕ = 5 см, Д = 110є.

Подсказка. Перед построением треугольника необходимо сделать «от руки» чертеж треугольника, где показаны все заданные элементы.

4. Построение треугольника по стороне и прилежащим к ней углам.

Дано

Требуется построить

Построение

1. Произвольно начертить отрезок АВ, равный заданному отрезку c.
2. Построить угол А, равный заданному.
3. Построить угол В, равный заданному.

Точка пересечения двух сторон углов А и В – вершина треугольника С.

Построили треугольник АСВ по стороне и двум заданным углам.

Самостоятельная работа к схеме 4.

Построить треугольник КМО, если КО = 6 см, К = 130є, О = 20є.

Построить треугольник ВСР, если С = 15є, Д = 50є, СД = 3 см.

5. Построение треугольника по трем сторонам.

Дано

Требуется построить

Построение

1. Построить отрезок АВ, равный заданному отрезку c.
2. Из точки А провести часть окружности, радиус которой
равен заданному отрезку b.
3. Из точки В провести часть окружности, радиус которой
равен заданному отрезку a, обе окружности пересекаются в точке С.

Построили треугольник АСВ по трем сторонам.

Самостоятельная работа к схеме 5.

Построить треугольник ОДЕ, если ОД = 4 см, ДЕ = 2 см, ЕО = 3 см.

Построить треугольник МНО, если МН = 1 см, НО = 4 см, ОМ = 3 см.

После построения любого треугольника, самостоятельно провести доказательство того, что получившийся треугольник – искомый, и по возможности провести исследование.

Построение треугольников. Задачи на построение

Вы будете перенаправлены на Автор24

Решение задач на построение состоит из четырех основных этапов:

Каждый этап является важным. Например, анализ и исследование задачи необходимы для рассмотрения случаев, когда задача будет иметь решение, а когда – нет.

Построение фигур проще выполнять с помощью транспортира и линейки с делениями, но в математике необходимо уметь выполнять построение, используя циркуль и линейку без делений.

Построение отрезка, равного заданному

Построить отрезок, равный заданному, можно за 3 действия. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить отрезок, который будет равен отрезку $АВ$. Для этого:

1. Отметим произвольно точку $А_1$ и проведем луч с началом в этой точке.
2. С помощью циркуля измерим заданный отрезок $АВ$.
3. Проведем часть окружности с радиусом, равным отрезку $АВ$, и центром в точке $А_1$. В точке пересечения окружности и построенного луча получим точку $В_1$.

Таким образом, построенный отрезок $А_1 В_1$ будет равен заданному отрезку $АВ$.

Построение угла, равного заданному

Построить угол, равный заданному, можно за $5$ действий. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить угол, который будет равен углу $А$.

1. Отметим произвольную точку $А_1$ и проведем из нее луч $А_1$.
2. Циркулем с произвольным радиусом проведем часть окружности с центром в точке $А$ до пересечения обеих сторон заданного угла $А$.
3. С тем же радиусом проведем часть окружности с центром в точке $А_1$ до пересечения с лучом $А_1$.
4. Из точек пересечения проведем окружности с одинаковым радиусом.
5. Проведем прямую из точки $А_1$ через вторую точку пересечения.

Готовые работы на аналогичную тему

Построение треугольника по двум сторонам и углу между ними

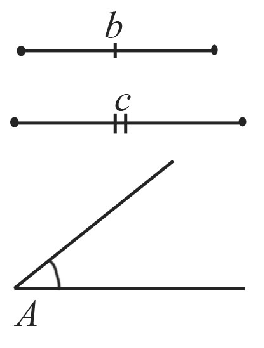
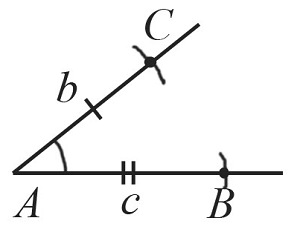
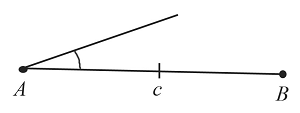
Пусть даны два отрезка $b$ и $с$ и угол $А$:

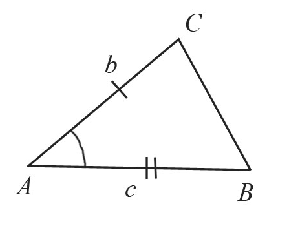
Необходимо построить треугольник с заданными двумя сторонами и углом между ними:

Построение выполняется в 4 этапа, каждый из которых показан на рисунках:

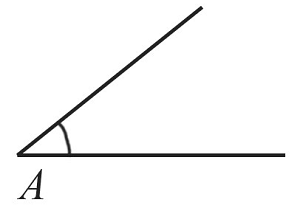
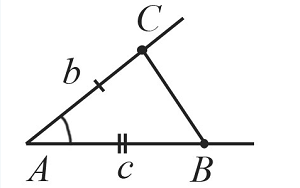
Построим угол $А$, который равен заданному углу по схеме, которая рассматривалась выше.

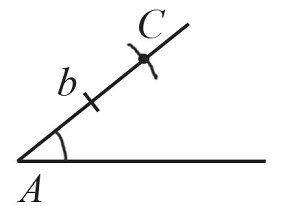
С помощью циркуля замеряем отрезок $b$ и отложим от точки $А$ такой же отрезок на одной из сторон построенного угла. Получим точку $С$.

Циркулем замеряем отрезок $с$ и отложим от точки $А$ такой же отрезок на второй стороне построенного угла. Получим точку $В$.

С помощью линейки соединим точки $В$ и $С$.

Таким образом, получили треугольник $АВС$, построенный по двум сторонам и углу между ними.

Для облегчения построения полезно схематически изобразить будущий треугольник со всеми необходимыми элементами. Так будет наглядней видно, что после чего нужно строить.

Построение треугольника по стороне и прилегающим к ней углам

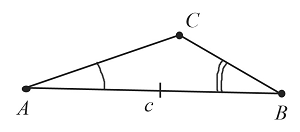
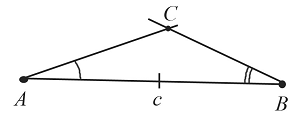
Пусть даны два угла $А$ и $В$ и отрезок $с$:

Необходимо построить треугольник с заданными двумя углами и стороной, к которой они прилегают:

Построение выполняется в $3$ этапа, каждый из которых показан на рисунках:

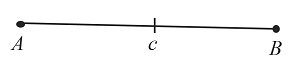
Начертим произвольный отрезок $АВ$, который равен заданному отрезку $c$.

Построим угол $А$, который равен заданному, как показано выше.

Построим угол $В$, который равен заданному.

Точка пересечения двух сторон построенных углов $А$ и $В$ является вершиной треугольника $С$.

Таким образом, получили треугольник $АВС$, построенный по стороне и двум углам.

Построение треугольника по трем сторонам

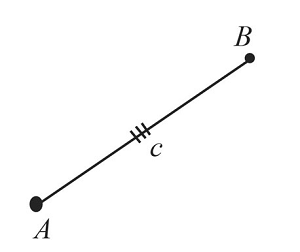
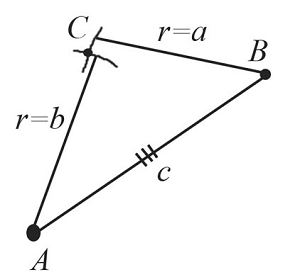
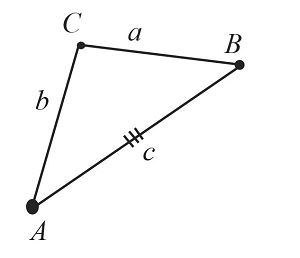
Пусть даны $3$ отрезка $а$, $b$ и $с$.

Необходимо построить треугольник по трем заданным сторонам.

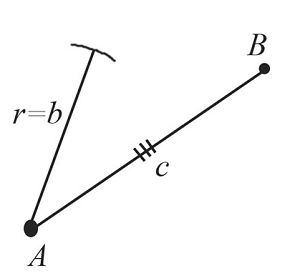
Построим отрезок $АВ$, который равен заданному отрезку $c$.

Из точки $А$ проведем часть окружности с радиусом, равным заданному отрезку $b$.

Из точки $В$ проведем часть окружности с радиусом, равным заданному отрезку $a$. Пересечением обеих окружностей является точка $С$.

Таким образом, получили построенный треугольник $АВС$ по трем заданным сторонам.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021

Геометрия. 7 класс

Конспект урока

Построение треугольника по трём элементам

Перечень вопросов, рассматриваемых в теме:

• Задачи на построение циркулем и линейкой.
• Алгоритмы решения простейших задач на построение.
• Способы решения задач на построение треугольника по трём заданным элементам.
• Этапы решения задач на построение: анализ, построение, доказательство, исследование.

Задачей на построение называется предложение, указывающее, по каким данным, какую геометрическую фигуру требуется построить, чтобы эта фигура удовлетворяла определённым условиям.

Построение треугольника по трём элементам:

• по 2 сторонам и углу между ними;
• по стороне и двум прилежащим к нему углам;
• по трём сторонам.

Задачи на построение:

• позволяют моделировать те или иные практические ситуации
• устанавливают связь между геометрией и черчением, геометрией и рисованием.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения

Построение треугольника по трём элементам.

Чтобы построить треугольник, нужно уметь строить:

1. Отрезок, равный данному.

2. Угол, равный данному.

Любая задача на построение включает в себя четыре основных этапа.

Анализ: предположить, что задача решена, сделать чертеж от руки искомой фигуры, составить план решения задачи.

Построение: описать способ построения.

Доказательство: доказать, что построенная фигура или множество точек – искомые.

Исследование: выяснить, всегда ли построение возможно.

Построить треугольник по трём заданным сторонам.

Построить треугольник по двум сторонам и углу между ними.

Построить треугольник по стороне и двум прилежащим к ней углам.

Разбор решения заданий тренировочного модуля.

Задача 1. Найдите расстояние от вершины В до прямой АС.

Дано. В треугольнике АВС: АВ = ВС = 10 см, ∠АВС = 120°.

∆АВС – равнобедренный. ВН – расстояние от точки В до прямой АС, т. е. ВН ⊥ АС. В равнобедренном треугольнике высота является биссектрисой. ∠АВН = 120°: 2 =60°, значит, ∠А = 30°. Против угла 30° лежит катет ВН равный половине гипотенузы АВ. Значит, ВН = 10 : 2 = 5 см.

Ответ: 5 см расстояние от вершины В до прямой АС.

Задача 2. Построить прямоугольный треугольник по гипотенузе и острому углу.

Дано: отрезок р, угол α.

1. Построим ∠В = α.
2. Проведем окружность с центром В и радиусом р.
3. С – точка пересечения окружности и угла.
4. Построим перпендикуляр к другой стороне угла.
5. ∆АВС – искомый.

Задача 3. Построить треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведенной из вершины этого угла.

Дано: отрезки р и q, угол α.

Требуется построить треугольник АВС, у которого одна из сторон, например АС = р, ∠А =α , а биссектриса АD = q.

📽️ Видео