1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание
Видео:Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрияСкачать  Geogebra — бесплатное он-лайн геометрическое приложениеGeogebra — наилучшее он-лайн геометрическое приложение для рисования геометрических фигур. Открыть в полный экран Видео:Построение точек по координатамСкачать  Построение треугольника по трем элементамВидео:Построение треугольника в трёх проекцияхСкачать  Задачи на построениеШирокое распространение в геометрии получили задачи на построение. Суть этих задач состоит в следующем: при заданных начальных условиях нужно построить тот или иной геометрический объект при помощи линейки и циркуля. Разберем общие принципы решения данных задач: Анализирование задачи. На этом этапе необходимо установить взаимосвязь между заданными условиями и объектом, который нужно изобразить. Результатом выполнения этого этапа является план решения задачи. Построение. Согласно разработанного плана выполняется построение объекта. Доказательство. На этом этапе необходимо доказать, что изображенная фигура полностью соответствует заданным условиям. Сложно разобраться самому? Попробуй обратиться за помощью к преподавателям Изучение. На этом этапе выполняется анализ начальных условий и определение, при каких условиях задача решается одним способом, при каких двумя, а при каких – вовсе не решаема. Разберем задачи на построение треугольника по трем различным начальным условиям. Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Изображение треугольника, если задана одна сторона и два прилегающих к ней углаЗадана одна сторон треугольника (BC) и прилежащие к ней углы (∝) и (β) , необходимо построить треугольник. 1. Анализируем условия. Необходимо построить треугольник (ABC) , имея одну сторону (BC) и углы (∠K= ∝ и ∠M= β) к ней прилежащие. Разработаем план решения задачи:
2. Строим треугольник 3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере. 4. Изучение. Заданные углы могут быть построены и в противоположную сторону, соответственно мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма всех углов треугольника должна равняться 180 0 , если сумма углов (∝) и (β) будет равна или больше 180 0 , решения задача не будет иметь. Видео:Как построить точки в системе координат OXYZСкачать  Изображение треугольника, если заданы три стороныЗаданы три стороны треугольника (AB) , (AC) и (BC) , нужно построить треугольник. 1. Анализируем условия. Необходимо построить треугольник (ABC) , имея три стороны (AB) , (AC) и BC. Разработаем план решения задачи:
2. Строим треугольник: 3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере. Не нашли что искали? Просто напиши и мы поможем 4. Изучение. Построенные окружности имеют две точки пересечения, поэтому мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма двух сторон треугольника всегда больше, чем третья его сторона, можно сделать вывод, если это условие не будет выполнено для заданных сторон, то задача не будет иметь решение. Видео:Построение треугольников по трем заданным точкам.Скачать  Изображение треугольника, если заданы две стороны и угол между нимиЗаданы две стороны треугольника (AB) и (AC) , а также угол ∝ между ними, необходимо построить треугольник. 1. Анализируем условия. Необходимо построить треугольник (ABC) , имея стороны (AB) и (AC) , а также угол (CAB) , равный (∝) . Разработаем план решения задачи:
2. Строим треугольник: 3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере. 4.Изучение. Прямая a бесконечна, поэтому таких треугольников можно изобразить очень много, но учитывая тот факт, что они все одинаковые, будем считать, что задача имеет одно решение. При условии, если угол (∝) будет равен или больше 180 0 , решения задача не будет иметь, так как сумма всех углов треугольника должна равняться 180 0 . 📽️ ВидеоЧастное положение точек. Точки принадлежащие к плоскостям проекции.Скачать  Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать  Как строить сеченияСкачать  Математика это не ИсламСкачать  Построение проекции пирамиды. Метод прямого треугольника.Скачать  Строим треугольник по трем сторонам (Задача 5).Скачать  Построение треугольника по трем сторонам. 7 класс.Скачать  Построение треугольника, равного данномуСкачать 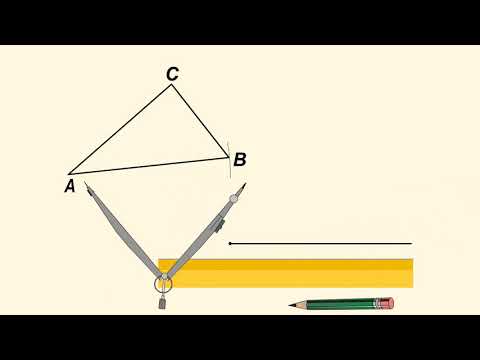 Построение окружности по трём точкам.Скачать  ЗАДАЧИ ПО ОСНОВАМ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ. МЕТОДЫ ПРОЕЦИРОВАНИЯ И ЭПЮРЫ ТОЧЕК. №1Скачать  Геометрия - Построение правильного треугольникаСкачать  Как строить сечения тетраэдра и пирамидыСкачать  Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать  Задание: ЭпюрСкачать  | ||


