Рассмотрим 1/4 круга.
Несколько названий обычных углов.
Прямой угол. Угол в 90 градусов называется прямым углом.
Тупой угол это угол больше 90 градусов.
Острый угол это угол меньше 90 градусов .
О градусах, углах и различных рисунках
Половина окружности равна 180 градусам .
Смежные углы это углы, имеющие общую сторону и сумма которых равна 180 градусам. Зелёный и голубой углы имеют общую суммму 180 градусов.


В подобных треугольниках подобные углы имеют одинаковую величину. Это правило справедливо и для других многоугольников.

Фигуры не являются подобными
Фигуры не являются подобными

Сумма углов треугольника всегда равна 180 градусам

Сумма углов прямоугольника всегда равна 360 градусам

Сумма углов прямоугольника всегда равна 360 градусам
Сделай упражнения на вычисление углов и затем проверь себя с помощью теста 1.
ps . Не забудь сразу заполнить список твоих контрольных работ
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.
Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Окружность
Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Центр окръжности
Радиус: расстояние от центра окружности до его границы.
Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам. 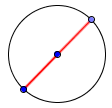
$d = 2cdot r$
Периметр (длина окружности): длина границы окружности. 
Длина окружности $= pi cdot$ диаметр $= 2 cdot pi cdot$ радиус
Длина окружности $= pi cdot d = 2 cdot pi cdot r$
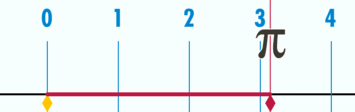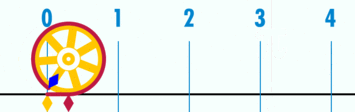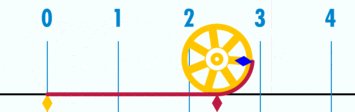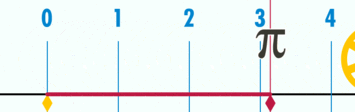
$pi$ — pi: число, равное 3,141592. или $approx frac$, то есть отношение $frac<text><text>$ любого окружности.
Дуга: изогнутая линия, которая является частью окружности. 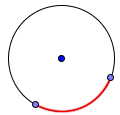
Дуги окружности измеряется в градусах или радианах.
Например: 90° или $frac$ — четверть круга,
180° или $pi$ — половина круга.
Сумма всех дуг окружности составляет 360° или $2pi$
Хорда: отрезок прямой, соединяющей две точки на окружности.
Сектор: похож на часть пирога (клин).
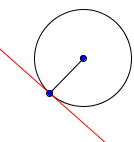
Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.
Формулы
Длина окружности $=pi cdot text = 2cdot pi cdot text$
Площадь круга $= pi cdot$ радиус 2
Радиус обозначается как r , диаметр как d , длина окружности как P и площадь как S .
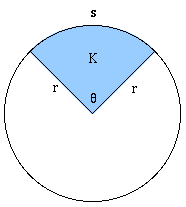
Площадь сектора круга
Площадь сектора круга K : (с центральным углом $theta$ и радиусом $r$).
Если угол $theta$ в градусах, тогда площадь = $frac pi r^2$
Если угол $theta$ в радианах, тогда площадь, тогда площадь = $frac r^2$
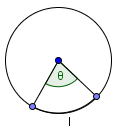
Центральный угол
Если длина дуги составляет $theta$ градуов или радиан, то значение центрального угла также $theta$ (градусов или радиан).
Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах . ) вы можете найти значение её соответствующего центрального угла ($theta$) по формуле:
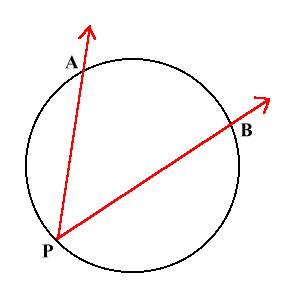
Вписанный угол
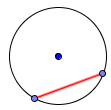
Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.
На рисунке, угол APB это вписанный угол.
Пример:
$widehat = 84^circ$
$angle APB = frac = 42^circ$
Углы между двумя хордами
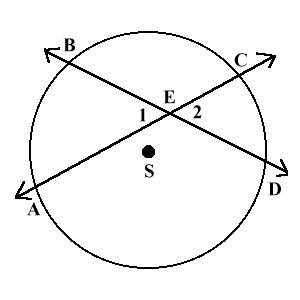
Случай 1: два секущие пересекаются внутри окружности.
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $frac(60^circ + 50^circ)=55^circ$
Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
$angle ABC =frac(x — y)$
На рисунке дуга AB=80° и дуги CD=30°.
$angle ABC = frac(80 — 30) = frac cdot 50 = 25^circ$
Хорды
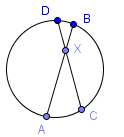
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:
🎦 Видео
Длина окружности. Математика 6 класс.Скачать

Что такое радиан?Скачать

Радиус и диаметрСкачать

10 класс, 11 урок, Числовая окружностьСкачать

РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Окружность, диаметр, хорда геометрия 7 классСкачать

7 класс, 9 урок, Градусная мера углаСкачать

ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Как искать точки на тригонометрической окружности.Скачать

Тригонометрическая окружность. Как выучить?Скачать

Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

+Как найти длину окружностиСкачать

8 класс. ОГЭ. Найти диаметр окружностиСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Перевод радиан в градусы (видео 12) |Окружность и Круг | ГеометрияСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать