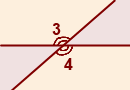
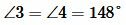Подобие треугольников вертикальные углы (7 видео)

Вертикальные углы. Свойства вертикальных углов

Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Содержание

Свойства вертикальных углов
Задачи и решения
Вертикальные углы
Подобные треугольники
Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
🎦 Видео

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

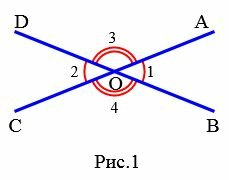
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

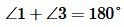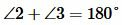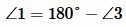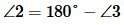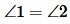
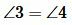
Следовательно . Аналогично доказывается, что .

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Задачи и решения

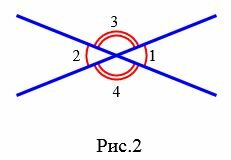
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

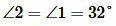
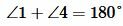
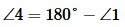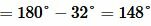Решение. Так как углы 1 и 2 вертикальны, то . Углы 1 и 4 смежные. Следовательно . Тогда

Углы 3 и 4 вертикальные. Тогда

Ответ. .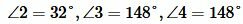

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

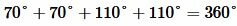Ответ. .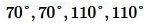

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Вертикальные углы

Какие углы вертикальные? Каким свойством обладают вертикальные углы?

Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.

Определение.

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

При пересечении двух прямых образуется две пары вертикальных углов:

∠1 и ∠2 — вертикальные углы

∠3 и ∠4 — вертикальные углы

Свойство вертикальных углов.

Вертикальные углы равны.

Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.

1) Сумма вертикальных углов равна 140º. Найти эти углы.

Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.

2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.

При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.

Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.

А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.

Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Подобные треугольники

Видео:Геометрия 8 Подобие треугольников - теорияСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.