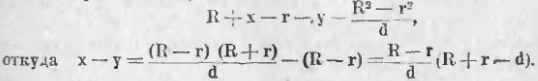Подобие окружностей как доказать

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

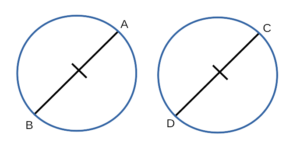
Первый признак равенства окружностей

Формулировка первого признака равенства окружностей:

Если диаметр одной окружности равен диаметру другой окружности,
то такие окружности равны.

Доказательство первого признака равенства окружностей:

1. Рассмотрим окружность с диаметром BA и окружность с диаметром DC, в которых BA = DC. Докажем,
   что окружность с диаметром BA и окружность с диаметром DC равны.
2. BA = DC, значит окружность с диаметром BA можно наложить на окружность с диаметром DC так, что они совместятся:
   окружность с диаметром BA совместится с окружностью с диаметром DC.
3. Итак, окружность с диаметром BA и окружность с диаметром DC полностью совместятся, значит они равны — ч.т.д

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

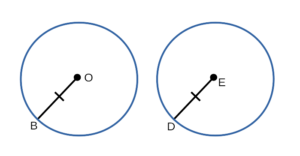
Второй признак равенства окружностей

Формулировка второго признака равенства окружностей:

Если радиус одной окружности соответственно равен радиусу другой окружности, то такие окружности равны.

Доказательство второго признака равенства окружностей:

1. Рассмотрим окружность с радиусом BO и окружность с радиусом DE, в которых BO = DE. Докажем,
   что окружность с радиусом BO и окружность с радиусом DE равны.
2. BO = DE, значит окружность с радиусом BO можно наложить на окружность с радиусом DE так, что они совместятся:
   окружность с радиусом BO совместится с окружностью с радиусом DE.
3. Итак, окружность с радиусом BO и окружность с радиусом DE полностью совместятся, значит они равны — ч.т.д.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

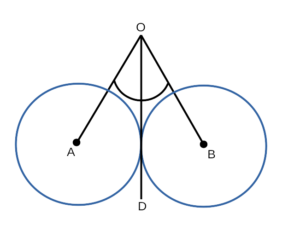
Третий признак равенства окружностей

Формулировка третьего признака равенства окружностей:

Если луч делит угол между центрами двух окружностей на два равных угла, то такие окружности равны.

Доказательство третьего признака равенства окружностей:

1. Рассмотрим луч OD, окружность с центром в точке A и окружность с центром в точке В, отрезки OA и OB, в которых ∠AOD = ∠BOD. Докажем,что окружность с центром в точке A и окружность с центром в точке B равны.
   
2. ∠AOD = ∠BOD, значит отрезки OA и OB можно наложить друг на другу так, что они совместятся:
   отрезок OA совместится с отрезком OB.
   
3. Итак, окружность с центром в точке A и окружность с центром в точке B полностью совместятся, значит они равны — ч.т.д.

Равенство окружностей можно доказать с помощью трех признаков:

1. По диаметру.
2. По радиусу.
3. По лучу и углу.

Видео:Найти подобные треугольники и доказать их подобие. Первый признак. Геометрия 8.Скачать

Математика

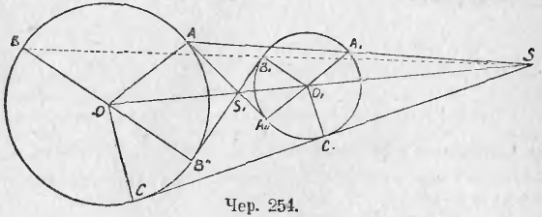
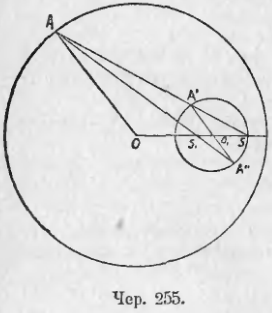
260. Возьмем два круга O и O₁ (чер. 254 и 255). Построим радиус OA и параллельный ему радиус другого круга O₁A₁, который имеет одинаковое направление с OA, или O₁A₁₁ тоже параллельный OA, но имеющий обратное с ним направление. Построим затем прямые AA₁ и AA₁₁, проходящие чрез концы этих радиусов. Тогда представляется следующая задача:

По данным радиусам R и r кругов и по расстоянию их центров OO₁ = d найти расстояние от одного из центров (напр., от O) точек пересечения линий центров с прямою AA₁ и с прямою AA₁₁.

Назовем OS чрез x; тогда O₁S = x – d. ∆OAS

∆O₁A₁S, следовательно, OS/O₁S = OA/O₁A₁ или x/(x – d) = R/r, откуда rx = Rx – dR.
Определяя отсюда x, получим

Отсюда мы видим, что положение точки пересечения S прямых OO₁ и AA₁ не зависит от того, в каком направлении от центра мы построили параллельные радиусы OA и O₁A₁, так что прямая BB₁, соединяющая концы другой пары параллельных радиусов OB и O₁B₁, должна пройти чрез точку S и, кроме того, имеем (∆O₁SB₁

∆OSB): SB₁/SB = r/R. Таким образом точка S обладает всеми свойствами внешнего центра подобия двух подобно расположенных фигур.

Также, называя OS₁ чрез y, получим S₁O₁ = d – y и из подобия ∆OAS₁ и ∆O₁A₁₁S₁: y(d – y) = R/r. Отсюда находим yr = dR – yR и

Отсюда видим, что положение точки S₁ также не зависит от того, какую именно пару параллельных, но идущих в обратных направлениях, радиусов мы взяли. Чрез эти же точку S₁ должна пройти прямая B₁B₁₁, соединяющая концы радиусов OB₁₁ и O₁B₁ параллельных, но имеющих обратные направления. Кроме того, имеем (∆O₁B₁S₁

Таким образом точка S₁ обладает всеми свойствами внутреннего центра подобия двух кругов.

Если один круг лежит внутри другого (чер. 255), то оба центра подобия расположены внутри меньшего круга: внешний лежит вне отрезка OO1, а внутренний — внутри его.

Центры O и O₁ также соответствуют друг другу, так как SO₁/SO = r/R (из подобия ∆OAS и ∆O₁A₁S) и S₁O₁/S₁O = r/R (из подобия ∆S₁O₁A₁₁ и ∆S₁OA).

Итак, всякие два круга подобно расположены и имеют два центра подобия — внутренний и внешний; центру одного круга соответствует центр другого и любой точке одного соответствует та точка другого, которая расположена на радиусе, параллельном радиусу первого круга, идущему чрез взятую точку, и имеющем то же или обратное направление. Обратно: если чрез S построить любую прямую A и соответствующие точки пересечения соединить с центрами, то полученные радиусы должны быть параллельны между собою.

261. Если окажется, что радиус, напр., O₁C₁ (чер. 254), перпендикулярен к прямой SC₁, то и радиус OC, соединяющий центр O другого круга с его точкою C, соответствующей точке C₁, должен быть также перпендикулярен к SC. Отсюда следует, что касательная из точки S к одному из наших кругов должна касаться и другого круга. Точно так же, если построим касательную к одному кругу чрез точку S₁, то она должна касаться и другого круга.

Этим пользуются для решения задачи: построить общую касательную к двум данным кругам .

Надо найти сначала их центры подобия, для чего надо построить радиус OA и параллельный ему диаметр A₁A₁₁ второго круга (чер. 254). Соединив концы A и A₁, найдем внешний центр подобия S и соединив A и A₁₁, найдем внутренний центр подобия S₁. Затем чрез найденные центры подобия S и S₁ построим касательные к одному кругу — они и должны быть общими касательными. Всего общих касательных у двух кругов может быть 4. Если два круга имеют внешнее касание, то точка касания служит их внутренним центром подобия, и общих касательных тогда будем иметь 3; если два круга пересекаются, то внутренний ценр подобия лежит внутри обоих кругов, и из него нельзя построить касательных, — тогда получим только две общих касательных чрез внешний центр подобия; если 2 круга имеют равные радиусы, то внешний центр подобия удаляется в бесконечность и тогда две внешних касательных параллельны линии центров; если два круга имеют внутреннее касание, то точка касания служит их внешним центром подобия, — тогда возможна лишь одна общая касательная; если, наконец, один круг внутри другого, то оба центра подобия расположены внутри обоих кругов, и общих касательных вовсе не существует.

262. Можно применить понятие о центре подобия кругов к решению задачи, которую раньше мы решили другим способом (п. 227 зад. 3): построить круг, касающийся двух пересекающихся прямых и проходящий чрез данную точку .

Точка пересечения данных прямых является внешним центром подобия искомого круга и какого-либо еще касающегося данных прямых и расположенного внутри того же угла, где лежит данная точка, но не проходящего чрез эту точку. Последний круг легко построить. Затем найдем на нем точку, соответствующую данной, построим чрез найденную точку радиус построенного круга, а чрез данную точку построим прямую, параллельную этому радиусу, — точка пересечения ее с биссектором угла и должна быть центром искомого круга. Задача имеет 2 решения, так как у построенного сначала круга можно найти 2 точки, любую из которых можно принять за соответствующую данной.

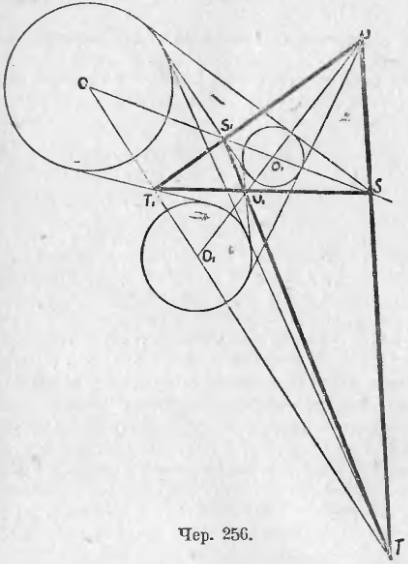
263. Если возьмем три каких-либо круга O, O₁ и O₂ (чер. 256), то они попарно подобно расположены и к ним применимо свойство п. 256. У этих трех кругов всего 6 центров подобия и они располагаются на четырех прямых: UST, US₁T₁, SU₁T₁ и TS₁U₁. Чрез каждый центр подобия проходят 2 из этих четырех прямых.

264. Степень точки относительно круга . В п. 222 мы познакомились с понятием о степени точки относительно круга. Этим именем называется, как мы знаем, произведение отрезков какой-либо прямой, проходящей чрез эту точку и пересекающей круг, от этой точки до точек пересечения прямой с кругом. Если точка вне круга, то это произведение равно квадрату касательной из нашей точки к ругу; если точка внутри круга, то это произведение равно квадрату половины хорды, делящейся в этой точке пополам. Чтобы отличить первый случай от второго, считают степень точки во втором случае отрицательною и перед указанным квадратом половины хорды ставят знак минус.

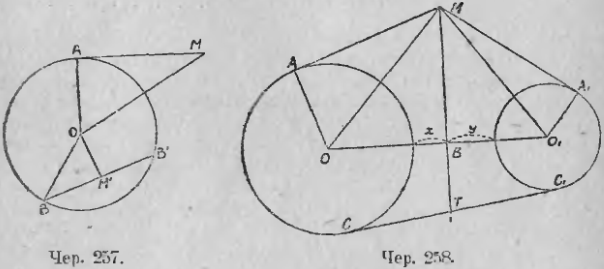
Пусть имеем круг O (чер. 257) и точку M вне его. Построив касательную MA и прямые MO и OA, найдем из прямоугольного треугольника AOM, что степень точки M = MA 2 = OM 2 – OA 2 = OM 2 – R 2 , где OA обозначаем чрез R.

Возьмем теперь точку M₁ внутри круга. Степень этой точки равна произведению отрезков хорды M₁B и M₁B’, взятому со знаком минус. Если эта хорда перпендикулярна к прямой OM₁, соединяющей точку M₁ с центром, то хорда делится в точке M₁ пополам и M₁B₁ = M1B и, следовательно, степень точки M₁ = –M₁B 2 . Из прямоугольного треугольника OM₁B найдем: M₁B 2 = OB 2 – OM₁ 2 = R 2 – OM₁ 2 , а, следовательно, степень точки M₁ = – M₁B 2 = –(R 2 – OM₁ 2 ) = OM₁ 2 – R 2 .

В обоих случаях степень точки выражается одинаково: она равна квадрату расстояния точки от центра минус квадрат радиуса.

Если точка лежит на круге, то легко увидим, что ее степень равна нулю.

265. Пусть теперь имеем 2 круга O и O₁ (чер. 258). Возникает вопрос, не существует ли таких точек, степени которых относительно обоих кругов равны между собой. Если такие точки существуют, то где они расположены? Допустим, что M такая точка. Называя радиус OA чрез R и радиус O₁A₁ чрез r, имеем для этой точки M

Из этого равенства и их равенства OB + O₁B = d мы можем определить отрезки OB и O₁B, — получим для каждого одно решение (уравнения первой степени), откуда заключаем, что точка B вполне определена. Отсюда выводим: если бы мы нашли другую точку M₁, степени которой относительно наших кругов равны, и на нее опустим перпендикуляр на линию центров, то он должен пройти чрез ту же точку B и, следовательно, слиться с MB. Следовательно, все точки, степени которых относительно двух кругов равны, расположены на перпендикуляре к линии центров. Этот перпендикуляр носит название — радикальная ось двух кругов. Обратно, легко показать, что всякая точка перпендикуляра MB имеет равные степени относительно наших кругов.

Из равенства (2) видим: 1) если R = r, то OB – O₁B = 0 и OB = O₁B, т. е. радикальная ось двух равных кругов делит расстояние между их центрами пополам; 2) если R > r, то OB > O₁B, т. е. радикальная ось расположена ближе к центру меньшего круга.

Но, если мы назовем чрез x и y расстояния точки B от круга O и от круга O₁ (мы применяемся к случаю данному на чертеже: круги расположены один вне другого), то OB = R + x, O₁B = r + y и, подставив в равенство (2), найдем:
f48

У нас R + r 0 (ибо считаем, что R > r). Тогда из последнего равенства вытекает x 2 = TC₁ 2 , или TC = TC₁, т. е. общая касательная двух кругов делится радикальною осью пополам.

Если два круга пересекаются, то радикальная ось должна пройти чрез точки пересечения, так как степень каждой из этих точек одинакова относительно каждого круга (она равна нулю); для построения радикальной оси в этом случае следует лишь построить прямую, определяемую этими точками пересечения.

Если два круга касаются, то радикальная ось есть перпендикуляр к линии центров чрез точку касания.

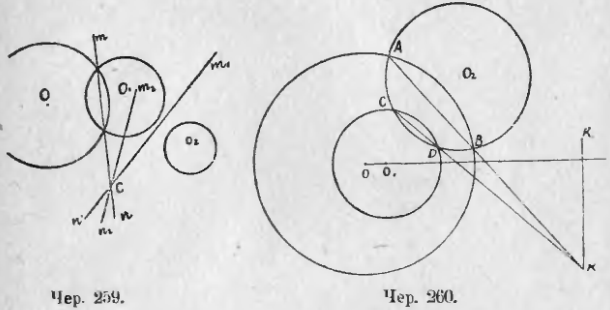
266. Пусть имеем 3 круга O, O₁ и O₂ (чер. 259). Построив радикальные ости mn и m₁n₁ двух пар кругов, мы найдем, что они пересекаются в какой-либо точке C, если только центры всех трех кругов не расположены на одной прямой. Так как точка C лежит на оси m₁n₁, то степени ее относительно кругов O₁ и O₂ одинаковы. Отсюда следует, что точка C имеет одинаковые степени и относительно кругов O и O₂, т. е. она должна лежать на радикальной оси последней пары кругов. Итак,

Радикальные оси трех кругов, взятых попарно, пересекаются в одной точке, которая называется радикальным центром трех рассматриваемых кругов.

Если из радикального центра построить касательные ко всем трем кругам, то они равны между собою.

Если три круга попарно пересекаются, то их общие хорды проходят чрез одну точку (общая хорда двух пересекающихся кругов есть их радикальная ось).

267. Свойством предыдущего п. можно воспользоваться для построения радикальной оси для двух непересекающихся кругов . Пусть даны круги O и O₁ (чер. 260). Построим третий круг O₂ чтобы его центр не лежал на линии центров OO₁ и чтобы он пересекался с каждым из данных кругов: с кругом O и точках A и B и с кругом O1 в точках C и D. Тогда AB есть радикальная ось кругов O и O₂, CD — радикальная ось кругов O₁ и O₂, точка пересечения K прямых AB и CD есть радикальный центр наших трех кругов. Построив прямую KK₁ ⊥ OO₁, получим радикальную ось кругов O и O₁.

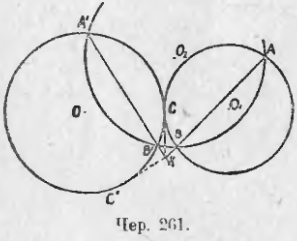
268. Построить круг, касающийся данного круга и проходящий чрез две данных точки .

Пусть дан круг O и точки A и B (чер. 261). Воспользуемся предыдущею задачею. Искомый круг должен касаться данного; следовательно, радикальною осью этой пары кругов должна служить их общая касательная. Если бы ее удалось построить, то легко было бы построить и искомый круг. Для построения этой радикальной оси воспользуемся, как в предыдущем п., третьим кругом O₂, пересекающим и данный и искомый круг. Но у искомого круга мы знаем пока только 2 точки A и B; следовательно, и этот третий круг O₂ мы можем построить лишь так, чтобы он проходил чрез точки A и B. Итак, построим любой круг O₂, проходящий чрез точки A и B и пересекающий круг O, напри., в точках A’ и B’. Тогда прямая AB есть радикальная ось искомого круга и круга O₂, прямая A’B’ есть радикальная ось кругов O и O₂, а точка их пересечения K есть радикальный центр всех трех кругов. Теперь нетрудно построить радикальную ось круга O и искомого, так как она должна касаться круга O: надо чрез точку K построить касательную к кругу O, а их можно построить две KC и KC’ (C и C’ точки касания). Тогда получим два решения: 1) искомый круг определяется точками A, B и C и 2) искомый круг определяется точками A, B и C’.

269. Мы имеем в виду решить еще две задачи на построение кругов: 1) построить круг, касающий двух данных кругов и проходящий чрез данную точку; и 2) построить круг, касающийся трех данных кругов (задача Аполлонин). Для этого надо познакомиться еще с некоторыми свойствами центра подобия и радикальной оси двух кругов.

Чрез центр подобия S кругов O и O₁ (чер. 262) построена общая касательная SCC₁ к этим кругам и секущая SB, соответственные точки которой суть A и A₁, B и B₁.

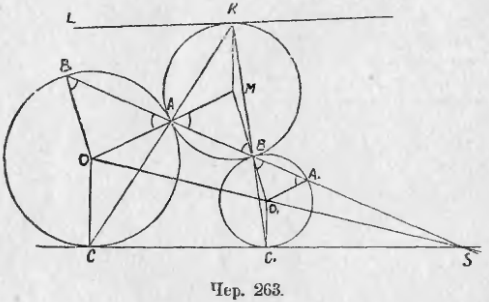
270. Пусть круг M касается кругов O и O₁ (чер. 263), обоих внешним образом в точках A и B. Построим прямую AB и пусть эта прямая пересекает еще круг O в точке B₁ и круг O₁ в A₁. Тогда OAM есть прямая, — следовательно, углы при основаниях в равнобедренных треугольниках OAB₁ и MAB равны; также O₁BM есть прямая и, следовательно, углы при основании в равнобедренном треугольнике O₁A₁B равны углам в ∆MAB (на чертеже равные углы отмечены). Отсюда заключаем, что O₁A₁ || OA и O₁B || OB₁, откуда следует, что прямая B₁ABA₁ проходит чрез внешний центр подобия кругов O и O₁. Итак, если круг касается двух других, то точки касания расположены на прямой, проходящей чрез центр подобия, но не суть соответственные точки .

Мы разобрали случай, когда M с O и с O₁ имеет внешнее касание; также будет и для случая, когда M с O и с O₁ имеет внутреннее касание; но если M имеет с одним из кругов внешнее касание, а с другим внутреннее, то вместо внешнего центра подобия надо взять внутренний. Поэтому в предыдущем заключении мы и не указали, чрез какой именно центр подобия проходит прямая, соединяющая точки касания.

Если построить еще общую касательную SC₁C, то прямые CA и C₁B, как мы знаем, пересекаются в точке K, лежащей на радикальной оси кругов O и O₁. Но можно выяснить еще, что точка K лежит на круге M.

Точка A есть внутренний центр подобия кругов O и M, причем точке O соответствует точка M, радиус OC (который ⊥ SC) соответствует некоторый радиус MX круга M, который параллелен OC, но имеет обратное с ним направление. Точка B есть внутренний центр подобия кругов O₁ и M, причем точке O₁ соответствует точка M и радиус O₁C₁ круга O₁ соответствует некоторый радиус MY круга M, который параллелен радиусу O₁C₁, но имеет обратное с ним направление. Отсюда следует, что радиусы MX и MY параллельны друг другу (ибо O₁C₁ || OC) и одинаково направлены, но они имеют общую точку M, — следовательно, они совпадают. С другой стороны, точка X должна лежать на прямой CA и точка Y на прямой C₁B. Поэтому совпадение радиусов MX и MY требует, чтобы точка X и точка Y совпали с точкою K, где пересекаются прямые CA и C₁B. Следовательно, точка K есть конец радиуса MK круга, и M, и K лежит на круге M.

Далее прямой SC относительно центра подобия A должна соответствовать прямая KL, проходящая чрез K (ибо SC проходит чрез C) и параллельная SC. Кроме того, прямая KL ⊥ MK, ибо SC ⊥ OC (радиусы OC и MK соответствуют друг другу). Поэтому прямая KL касается круга M в точке K. К тому же результату придем, рассматривая соответствие относительно центра подобия B.

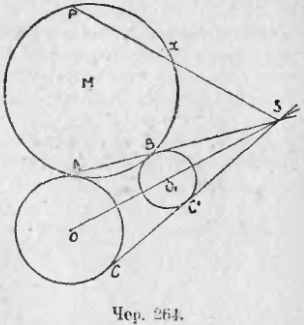
271. Теперь мы можем приступить к решению первой из намеченных задач: даны круги O и O₁ и точка P (чер. 264). Требуется построить круг, касающийся кругов O и O₁ и проходящий чрез P.

Пусть M искомый круг и точки A и B суть точки касания. Тогда легко найти точку X, где луч SP (S центр подобия кругов O и O1) пересекает круг M. Мы имеем:

SP · SX = SA · SB = SC · SC₁ (п. 269)

Отсюда SX/SC = SC1/SP, т. е. отрезок SX есть четвертый пропорциональный к трем известным отрезкам SC, SC1 и SP, — построить его мы умеем. Тогда задача сведется к задаче п. 268.

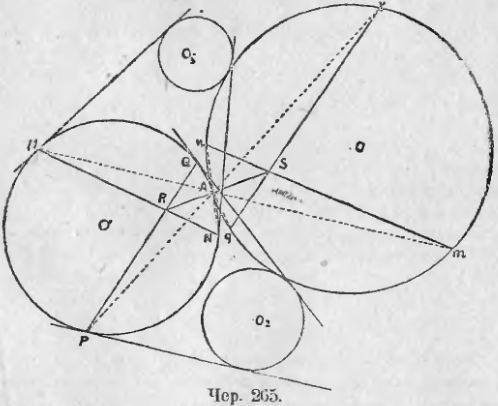
272. Задача Апполония . Даны три круга O₁, O₂ и O₃ (чер. 265). Построить круг, касающийся трех данных.

Мы будем рассуждать лишь в предположении, что мы ищем круг, касающийся каждого из данных внешним образом. Применить к другим случаям не представит затруднений (всего задача имеет 8 решений).

Пусть круг O есть искомый и A есть точка касания кругов O и O₁; тогда прямой MN, соединяющей точки касания M и N общих касательных для кругов O₁ и O₃, соответствует относительно центра подобия A (точка A есть внутренний центр подобия кругов O₁ и O) радикальная ось mn кругов O₁ и O₃: точке M соответствует точка m, лежащая на круге O и на радикальной оси кругов O₁ и O₃ (п. 270) и также точке N соответствует точка n, лежащая на радикальной оси кругов O₁ и O. Точно так же прямой PQ, соединяющей точки касания круга O₁ с общими касательными для кругов O₁ и O₂, соответствует радикальная ось pq кругов O₁ и O₂.

Точке R, где MN и PQ пересекаются, соответствует точка S, где mn и pq пересекаются, т. е. радикальный центр кругов O₁, O₂ и O₃. Поэтому точки R и S лежат на одной прямой с A.

Точки R и S мы можем построить; соединив их, получим (между ними) точку касания искомого круга с кругом O₁, после чего задача легко решается.

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Планиметрия. Страница 9

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать 1.Преобразование подобия и его свойства Преобразованием подобия называется преобразование фигуры G в фигуру G’, у которой расстояние между точками изменяется в одно и тоже число раз. Т.е. ОA’ = k OA. Это означает, что для любых двух точек геометрической фигуры выполняется равенство A’B’ = k AB. (Рис.1) Число k называется коэффициентом подобия. Если взять произвольную точку, например точку О. И отложить отрезок OB’ = k OB, то такое преобразование фигуры G в фигуру G’ называется гомотетией. А число k называется коэффициентом гомотетии. Таким образом, гомотетия есть преобразование подобия. Видео:Первый признак подобия треугольников. Доказательство. 8 класс.Скачать Свойства преобразования подобия Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые, отрезки в отрезки и при этом углы между прямыми сохраняются. Рис.2 Подобие фигур. Видео:Геометрия 8 класс. Второй признак подобия треугольниковСкачать Подобие треугольников по двум углам Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. (Рис.3) Докажем это утверждение. Пусть даны два треугольника ABC и A’B’C’. Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. Полученный треугольник A»B»C» равен треугольнику ABC по стороне и прилегающим к ней углам. Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. А т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’. Рис.3 Подобие треугольников по двум углам. Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать 3.Подобие треугольников по двум сторонам и углу между ними Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны. Докажем это утверждение. (Доказательство аналогично доказательству подобия по двум углам) Пусть даны два треугольника ABC и A’B’C’. Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. Полученный треугольник A»B»C» равен треугольнику ABC по двум сторонам и углу между ними со сторонами kA’B’=A»B» и kA’C’=A»C». Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. А т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’, т.е. kA’B’=AB, kB’C’=BC и kA’C’=AC. 6.Пример 1 Докажите, что фигура подобная окружности, есть окружность. Доказательство: Пусть даны две окружности F и F’ с радиусами R1 и R2 . Подберем коэффициент k так, чтобы kR1 = R2. Необходимо доказать, что окружности подобны. Зададим на плоскости систему координат с осями Оx и Oy таким образом, чтобы центр первой окружности F совпал с началом координат. Параллельным переносом переместим вторую окружность F’ так, чтобы ее центр также совпал с началом координат. На окружности F возьмем две произвольные точки А и В. И проведем между ними хорду. Также проведем к этим точкам радиусы ОА и ОВ, которые продлим до окружности F’, т.е. ОA’ и OB’. Оси Оx и Оy повернем так, чтобы ось Oy пересекала хорду под прямым углом (Рис.7). Тогда k OA = OA’. Теперь рассмотрим треугольник ОАС. Рис.7 Задача. Докажите, что фигура подобная окружности, есть окружность. Таким образом, мы пришли к выводу, что A’B’ = k AB. А это означает, что расстояние между любыми двумя точками окружности F’ в k раз больше, чем расстояние между подобными точками в окружности F, т.е фигуру F’ можно получить преобразованием подобия или гомотетией относительно точки О. А это значит, что окружности F и F’ подобны. Пример 2 У треугольников АВС и А1В1С1 ∠A = ∠A1, ∠B = ∠B1. AB = 6, AC = 9, A1B1 = 10, B1C1 = 10. Найдите остальные стороны треугольников. Решение: Пусть даны два треугольника АВС и А1В1С1 ∠A = ∠A1, ∠B = ∠B1 (Рис.8). Данные треугольники подобны по двум углам: ∠A = ∠A1 и ∠В = ∠B1. Отсюда следует, что все стороны второго треугольника отличаются от сторон первого треугольника в k число раз, т.е. коэффициент подобия. Найдем число k: k = AB / А1В1 = 6 / 10 = 3 / 5 Отсюда следует, что ВС = k * В1С1 = (3 / 5) * 10 = 6 см А1С1 = АС / k = 9 / (3 / 5) = 15 см Рис.8 Задача. У треугольников АВС и А1В1С1. Пример 3 В трапеции ABCD основание АD = 32 см, а основание ВС = 8 см. Угол между диагональю АС и стороной СD равен углу ∠АВС, т.е. ∠АВС = ∠АСD. Найдите диагональ АС. Решение: В трапеции два основания лежат на параллельных прямых (Рис.9). Отсюда следует, что угол ∠CAD = ∠BCA, как внутренние накрест лежащие углы. Следовательно, треугольники АВС и АСD подобны по двум углам: ∠AВС = ∠АCD по условию задачи, ∠CAD = ∠BCA, как внутренние накрест лежащие углы. Тогда можно составить следующие соотношение: k = АС / ВС = AD / AC . Следовательно, AC 2 = 8 * 32 = 256 Отсюда, АС = 16 см. Рис.9 Задача. В трапеции ABCD основание АD = 32 см. Пример 4 В остроугольном треугольнике АВС проведены высоты AD, BE, CF. Найдите углы треугольника DEF, если в треугольнике АВС ∠А = α, ∠В = β, ∠С = γ. Решение: Рассмотрим два прямоугольных треугольника AFC и ABE. Они подобны по одному острому углу, так как угол при вершине А у них общий. Следовательно, угол ∠FCE = ∠ABE. Обозначим его как ϕ3. Аналогичным образом обозначим: Рассмотрим два прямоугольных треугольника AFO и DOC. Они подобны по одному острому углу: углы при вершине О равны как вертикальные (Рис.10). Отсюда следует, что треугольники FOD и AOC также подобны по двум пропорциональным сторонам и углу между ними. Так как OD / OF = OC / AO Следовательно, OD / OС = OF / AO Отсюда следует равенство углов: Треугольники BFO и EOC подобны. У них углы при вершине О равны как вертикальные, а углы при вершинах F и E прямые. Отсюда следует подобие треугольников FOE и BOC. Следовательно, Рис.10 Задача. В остроугольном треугольнике АВС. Так как ϕ1 + ϕ2 + ϕ3 = 90° (из прямоугольного треугольника BFC), то в треугольнике FDE угол при вершине F равен: Аналогичным образом выводится, что: Пример 5 В треугольник ABC вписан ромб ADEF, таким образом, что угол А у них общий, а вершина Е находится на стороне ВС. АВ = 12 см, АС = 4 см. Найдите сторону ромба. Решение: Так как у ромба противоположные стороны параллельны, то треугольники АВС и DBE подобны по двум углам: ∠А = ∠D, ∠C = ∠E как соответственные (Рис.11). Тогда можно составить следующие соотношение: AC / DE = AB / (AB — AD) так как AD = DE, то AC / DE = AB / (AB — DE) 4 / DE = 12 / (12 — DE) 48 — 4 DE = 12 DE Отсюда, DE = 3 см. Рис.11 Задача. В треугольник ABC вписан ромб ADEF. 📽️ Видео №547. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.Скачать Подобные треугольники и окружностьСкачать Подобие треугольников Радиус вписанной окружностиСкачать Третий признак подобия треугольников. Доказательство. 8 класс.Скачать ЕГЭ Задание 16 Первый признак подобия треугольниковСкачать Второй признак подобия треугольников. Доказательство. 8 класс.Скачать #207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать Геометрия 8 класс. Первый признак подобия треугольниковСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности Главная > Учебные материалы > Математика: Планиметрия. Страница 9 1 2 3 4 5 6 7 8 9 10 11 12 Рис.1 Преобразование подобия и его свойства. Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать 2.Подобие фигур. Подобие треугольников по двум углам Две фигуры называются подобными, если преобразованием подобия они переходят друг в друга. (Рис.2) Если две фигуры подобны третьей, то они подобны друг другу. Из свойств преобразования подобия следует, что у подобных фигур, соответсвующие стороны пропорциональны и соответствующие углы равны. Рис.3 Подобие треугольников. Видео:Второй и третий признаки подобия треугольников (доказательство) - 8 класс геометрияСкачать 4.Подобие треугольников по трем сторонам Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. Доказательство. (Доказательство аналогично доказательству подобия по двум углам) Пусть даны два треугольника ABC и A’B’C’. Преобразованием подобия преобразуем треугольник A’B’C’ в треугольник A»B»C» с коэффициентом k, т.е. подвергнем гомотетии. В результате получим треугольник A»B»C», который равен треугольнику ABC по трем сторонам kA’B’=A»B», kВ’C’=В»C» и kA’C’=A»C». Т.к. преобразование подобия сохраняет углы, а расстояние между двумя точками изменяется в k раз. Следовательно треугольники A’B’C’ и A»B»C» подобны. И т.к. треугольники ABC и A»B»C» равны, то треугольник ABC подобен треугольнику A’B’C’. Рис.4 Подобие треугольников по трем сторонам. Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать 5.Подобие прямоугольных треугольников Если два прямоугольных треугольника имеют по одному равному острому углу, то такие треугольники подобны. Пусть дан прямоугольный треугольник ABC. Проведем высоту CD. Треугольники ABC и ADC подобны, т.к. угол А у них общий. Так же как и треугольники ADC и BDC. Следовательно: Т.е. катет прямоугольного треугольника равен средней геометрической гипотенузы и проекции этого катета на гипотенузу. А высота в прямоугольном треугольнике равна средней геометрической между проекциями катетов на гипотенузу. Отсюда можно сделать вывод, что в любом треугольнике биссектриса делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. (Свойство биссектрисы треугольника). Рис.5 Подобие прямоугольных треугольников. Докажем это утверждение. Пусть дан треугольник ABC. (Рис.6) BE — биссектриса. Треугольники ABE и BCD подобны. Углы В у них равны. Треугольники ADE и DCF также подобны. Углы D у них равны, как вертикальные. Отсюда можно записать следующие соотношения для двух пар треугольников. Т.е. отрезки AD и DC пропорциональны сторонам AB и BC. Рис.6 Подобие прямоугольных треугольников.