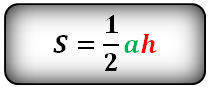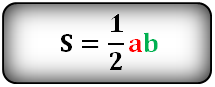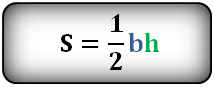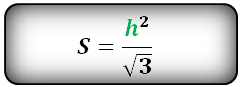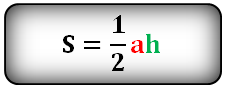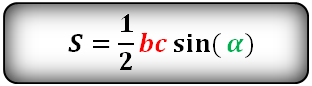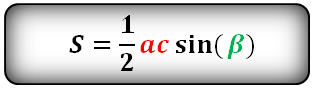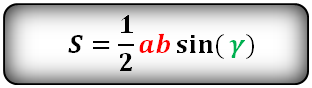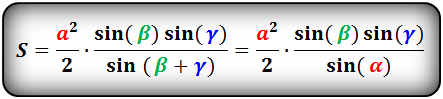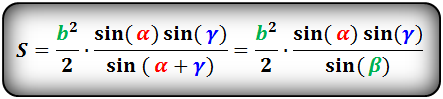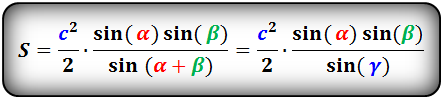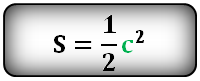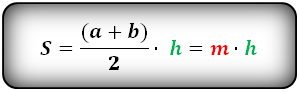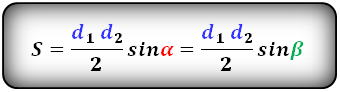Площадь треугольника через трапецию

Видео:Площадь параллелограмма, треугольника, трапецииСкачать

We are checking your browser. mathvox.ru

Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Площадь параллелограмма треугольника и трапецииСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d61759ef9a22de5 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Формулы площадей всех основных фигур

Видео:8 класс, 15 урок, Площадь трапецииСкачать

1. Формула площади круга через радиус или диаметр

Зная диаметр или радиус круга, можно найти его площадь.

r — радиус круга

D — диаметр

Формула площади круга, (S):

Видео:площадь ТРЕУГОЛЬНИКА площадь ПАРАЛЛЕЛОГРАММА площадь ТРАПЕЦИИ 8 классСкачать

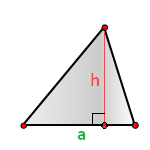
2. Формула расчета площади треугольника

h — высота треугольника

a — основание

Площадь треугольника (S):

Видео:Как выразить площадь трапеции через площади треугольников, ограниченных диагоналями и основаниями?Скачать

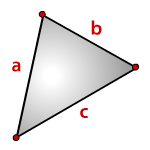
3. Площадь треугольника, формула Герона

a , b , c , — стороны треугольника

p— полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

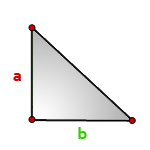
4. Площадь прямоугольного треугольника по катетам

Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b — катеты треугольника

Формула площади прямоугольного треугольника, (S):

Видео:Найти площадь треугольника, зная площадь трапецииСкачать

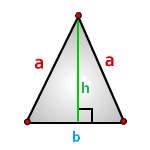
5. Как вычислить площадь равнобедренного треугольника ?

b — основание треугольника

a — равные стороны

h — высота

Формула площади треугольника через высоту h и основание b , ( S ):

Формула площади треугольника через, стороны a , b , (S):

Видео:ОГЭ Задание 24 Площадь треугольника, трапецииСкачать

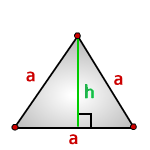
6. Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a — сторона треугольника

h — высота

Площадь треугольника только через сторону a , (S):

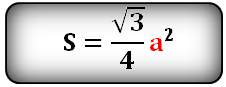
Площадь треугольника только через высоту h , ( S ):

Площадь треугольника через сторону a и высоту h , (S):

Видео:ПЛОЩАДЬ треугольника | ПЛОЩАДЬ трапеции | ОГЭ математикаСкачать

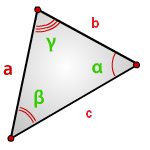
7. Найти площадь треугольника, угол и две стороны

Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

a , b , c — стороны треугольника

α , β , γ — углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

Видео:Найти площадь треугольника в трапеции #геометрия #егэ #огэ #математика #площадьСкачать

8. Площадь треугольника по стороне и двум углам, формула.

a , b , c — стороны треугольника

α , β , γ — противолежащие углы

Площадь треугольника через сторону и два угла (S):

Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

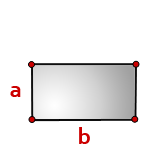
9. Формула расчета площади прямоугольника

b — длина прямоугольника

a — ширина

Формула площади прямоугольника, (S):

Видео:Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

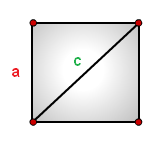
10. Как рассчитать площадь квадрата через диагональ или сторону

a — сторона квадрата

c — диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b — стороны параллелограмма

α , β — углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H _b — высота на сторону b

H _a — высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D — большая диагональ

d — меньшая диагональ

α , β — углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

Видео:Площадь трапеции.  Быстрый способ запомнить формулуСкачать

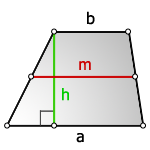
12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

m — средняя линия

h — высота трапеции

Формула площади трапеции, (S):

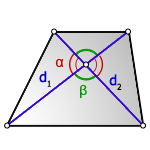
2. Формула площади трапеции через диагонали и угол между ними

d ₁, d ₂ — диагонали трапеции

α , β — углы между диагоналями

Формула площади трапеции, (S):

3. Формула площади трапеции через четыре стороны

b — верхнее основание

a — нижнее основание

c, d — боковые стороны

Формула площади трапеции, (S):

Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b — верхнее основание

a — нижнее основание

c — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α , β — углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α , β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m — средняя линия трапеции

c — боковая сторона

α , β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание

a — нижнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Видео:Трапеция. Отношение площадей треугольников. Свойства диагоналей трапецииСкачать

Площадь треугольника через трапецию

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.

$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Докажем, например, утверждение $$ 4.^$$ .

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).

По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`

(т. к. угол `BDK` — это угол между диагоналями трапеции).

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.

$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.

🔍 Видео

Сможешь найти площадь треугольника по площади трапеции?Скачать