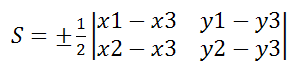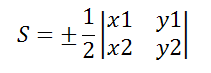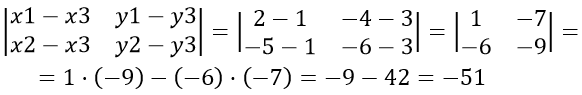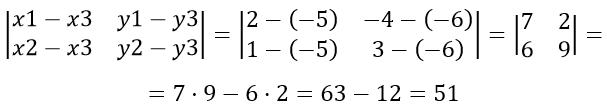Площадь треугольника через определитель

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

• делящий противоположную углу сторону пополам — медиана;
• разделяющий угол при вершине на два равных — биссектриса;
• падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

1. Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
2. Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

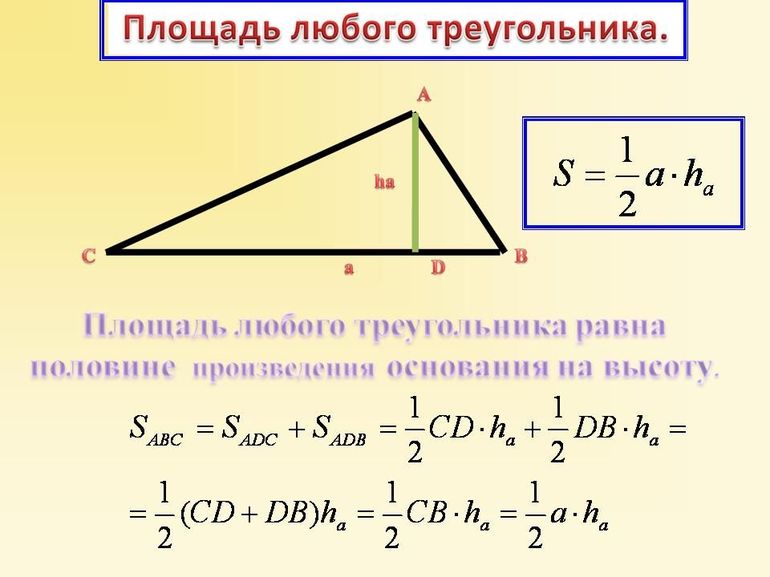
Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

Тогда координаты его векторов AB- и AC- выразятся так:

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

1. Необходимо определить координаты векторов, образующих стороны треугольника.
2. Затем, следует вычислить длины их сторон.
3. Посчитать полупериметр фигуры.
4. Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 2 + y1 2 )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

1. Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
2. Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Видео:площадь треугольника с помощью матрицы за 3 минуты для анимефагов от 3 до 99 летСкачать

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Видео:Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

Учебный материал «Площадь многоугольника через определить второго порядка» для элективного курса по математике, 10 класс.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Площадь треугольника, построенного на векторахСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Площадь многоугольника через определитель второго порядка.

Цель:1. Вывод формулы площади треугольника через определитель II -го порядка с применением формул тригонометрии.

2.Самостоятельная творческая работа по разработке формул площадей четырехугольника, пятиугольника, квадрата, правильного шестиугольника, n -угольника с использованием определителя II -го порядка.

3. Научить учащихся способу вычисления площади четырехугольника с координатами его вершин для использования на ЕГЭ.

I . Введение. На уроках алгебры мы познакомились с необычным способом решения систем двух линейных уравнений с двумя переменными с помощью определителя второго порядка.

Использование определителей оказалось удивительно полезным и интересным при решении и анализе систем.

А используется ли понятие определителя в геометрии?

Постараемся сегодня ответить на этот вопрос.

II . Объяснение нового материала. Вывод формулы площади треугольника через определитель II -го порядка в прямоугольной системе координат.

Определителем второго порядка называют значение разности произведений чисел

a ∙ d — b ∙ c , записываемых для удобства вычислений в виде таблички из четырех чисел..

Выведем формулу площади треугольника в виде определителя, составленного из разности координат вершин треугольника.

Докажем, что площадь треугольника равна:

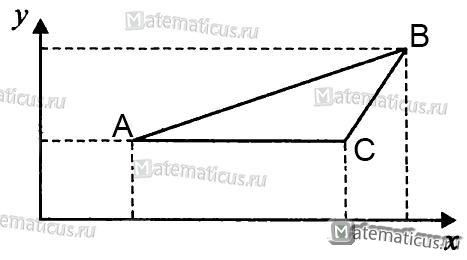
Пусть в прямоугольной системе координат А(х_1,у₁), В(х₂,у₂), С (х₃,у₃) – вершины треугольника. Найти площадь треугольника АВС.

Обозначим стороны треугольника через АС= b , АВ =с и угол между ними через ВАС=φ, по известной формуле тригонометрии получим: S = ½ b с∙ sinφ .

Угол φ можно представить в виде разности: φ = β-α, где α и β – углы, образованные соответственно сторонами АВ и АС с осью Ох.

Поэтому S =½ b с∙ sin ( β-α) =½ b с∙( sinβ ∙ cosα — cosβ ∙ sinα ).

Из рисунка имеем

Заметим, что эта формула при ином расположении вершин может дать площадь треугольника S со знаком «минус».

Поэтому формулу площади треугольника запишем в виде S =±½((х₂—х₁)(у₃-у₁)-(х₃-х₁)(у₂-у₁), где знак выбирается так, чтобы для площади получалось положительное число.

Используя понятие определителя второго порядка = а d — b с, формулу можно записать в удобной для запоминания форме:

S треуг. = ±.

Постановка проблемы: определить площадь четырехугольника , пятиугольника, квадрата, правильного шестиугольника, n -угольника через координаты их вершин.

Рекомендации: Определение площади многоугольника сводится к определению площадей треугольников. Для этого достаточно разбить многоугольник на треугольники, площади которых вычисляют по найденной формуле. Правильный шестиугольник разбивается на равные четырехугольники

II . Учащиеся. Самостоятельное решение проблемы (работа учащихся в группах дифференцировано: продвинутый уровень-площадь четырехугольника и пятиугольника, базовый уровень-площадь четырехугольника, шестиугольника, квадрата).

Выведем формулу для вычисления площади четырехугольника на примере трапеции.

Пусть трапеция задана координатами своих вершин в прямоугольной системе координат.

Диагональ разделит трапецию на два треугольника, площади которых найдем через определитель.

₌

_{Запишем выражение в удобной для запоминания форме, в виде определителя}

_{Вывод: Площадь четырехугольника равна половине определителя, элементами столбцов и строк которого является разность координат вершин четырехугольника, взятых по диагонали.}

_{Нумерацию координат можно рассмотреть в любом порядке.}

_{Пример. Вычислить площадь четырехугольника с координатами его вершин}

_{По формуле через определитель}

_{Сделаем проверку, вычислив площадь трапеции как сумму площадей, через высоты треугольников.}

_{Получили равные ответы.}

_{2. Площадь правильного шестиугольника.}

_{Площадь правильного шестиугольника найдем как сумму площадей двух равных четырехугольников.}

_{Площадь ромба, квадрата или параллелограмма находятся аналогично, разбиением фигуры на равные треугольники.}

_{.Если центр многоугольника расположен в начале координат, то формула площади многоугольника записывается с помощью координат одной или двух вершин:}

_{Площадь квадрата равна учетверенному произведению координат одной вершины треугольника.}

_{Площадь правильного восьмиугольника выражается через определитель с помощью координат двух вершин многоугольника}

_{4. Площадь пятиугольника. Выведем формулу для вычисления площади пятиугольника:}

умножая двучлены, получим

Раскроем скобки, приведем подобные слагаемые, которые при этом взаимно- уничтожаются, и получим:

Сгруппируем произведения относительно равных абсцисс или равных ординат, получим:

Поменяем знаки, получается в итоге:

.

Площадь пятиугольника равна сумме абсцисс вершин треугольника, умноженных на разность ординат соседних вершин.

5.Аналогично запишем формулу для n -угольника

Формула площади n — угольника через координаты своих вершин

Подведение итогов: Выступления учащихся.

1. Эрдниев О.П. Учебник для средней школы.

2.Кудрявцев В.А. Краткий курс высшей математики.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 937 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 496 412 материалов в базе

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Дистанционные курсы для педагогов

Другие материалы

• 06.10.2015
• 1895

• 06.10.2015
• 6823

• 06.10.2015
• 433

• 06.10.2015
• 1130

• 06.10.2015
• 618

• 06.10.2015
• 614

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 06.10.2015 3089 —> —> —> —>
• DOCX 140 кбайт —> —>
• Рейтинг: 2 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Бородина Татьяна Петровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 39591
• Всего материалов: 6

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Как найти площадь треугольника, зная координаты его вершины.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Свободное движение повышает креативность

Время чтения: 1 минута

Более 800 вузов проведут прием через суперсервис

Время чтения: 1 минута

Минспорта утвердило программу подготовки киберспортсменов

Время чтения: 1 минута

Школы Сургута переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Орловские школы переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Площадь треугольника на плоскости

Пусть точки A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) – вершины треугольника, тогда площадь треугольника выражается формулой

В формуле правая сторона — это определитель второго порядка.

Площадь треугольника является положительной величиной и поэтому перед определителем берём знак «плюс», в случае, если значение положительно, и минус в противном случае, то есть отрицательно.

Примечание
Если вершина C треугольника совпадает с началом координат, то есть x₃=y₃=0, то формула площади треугольника примет вид

Пример
Найти площадь треугольника с вершинами A(2;-4), B(-5;-6) и C(1;3)

Решение
Пусть примем A за первую вершину, B — за вторую и C — за третью, тогда находим:

,так как получился отрицательный знак, следовательно перед определителем берём знак «минус»

[S = ( — frac)cdot( — 51) = 25,5]

Если вершины треугольника переобозначим немного в другом порядке, допустим, первой вершиной A, второй вершиной C и третьей вершиной B, тогда получим выражение:

В этом случае, необходимо взять знак « плюс « и получим снова площадь треугольника S=25,5

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.5 / 5. Количество оценок: 2

🎦 Видео

Найти площадь треугольника на векторахСкачать

5 способов вычисления определителя ★ Какой способ лучше?Скачать

Вычислить определитель 3 порядка. Правило треугольникаСкачать

8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Как найти площадь треугольника без формулы?Скачать

Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать

Задача, которую исключили из экзамена в АмерикеСкачать

Математика это не ИсламСкачать

8 класс, 14 урок, Площадь треугольникаСкачать

Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Векторное произведение векторов. Площадь треугольника на векторахСкачать