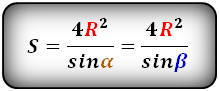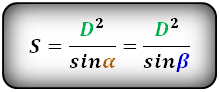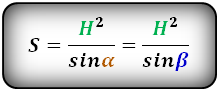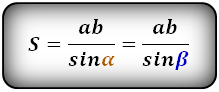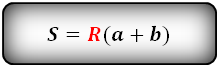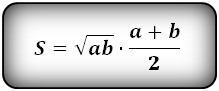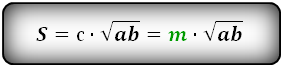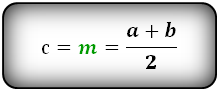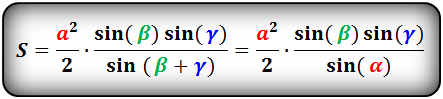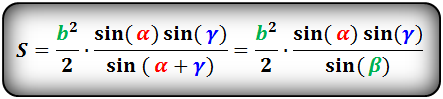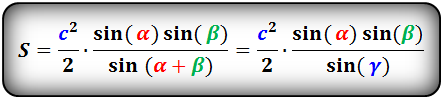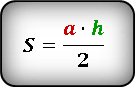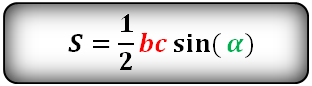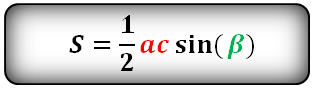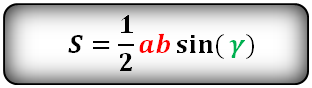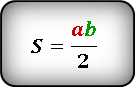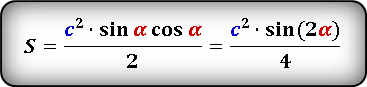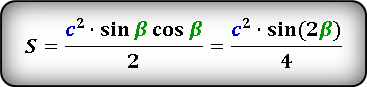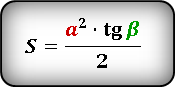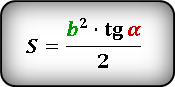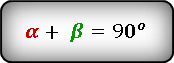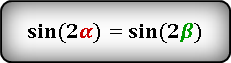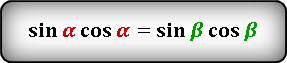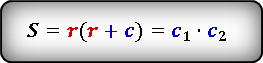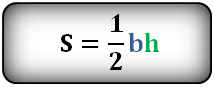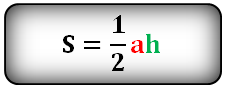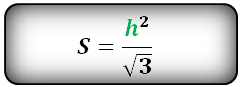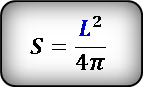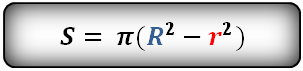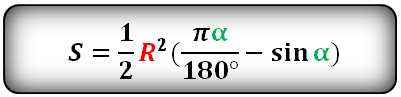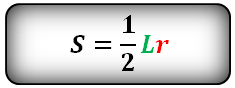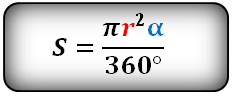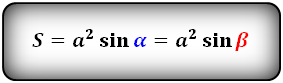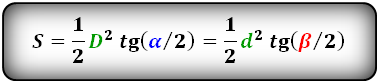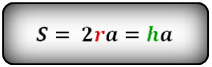Площадь треугольника через cos

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

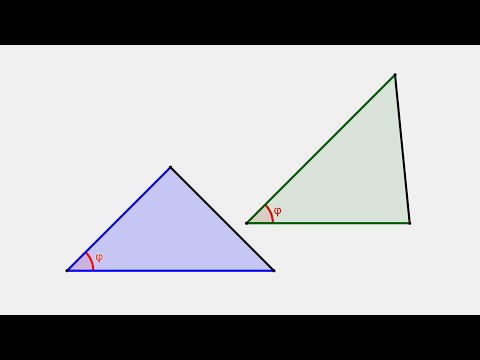
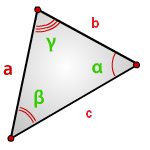
Площадь треугольника через две стороны и угол между ними, формула

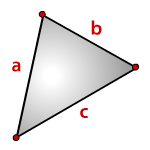
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Площадь треугольника через одну сторону и прилежащие к ней углы, формула

Если известна одна сторона треугольника и два прилежащих к ней угла, то площадь данного треугольника вычисляется, как половина квадрата данной стороны умноженная на дробь, в числителе которой, произведение синусов прилежащих углов, а в знаменателе синус противолежащего угла. Противолежащий угол вычисляется по формуле:

Площадь треугольника вычисляется по формулам:

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

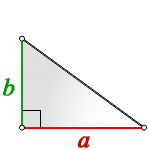
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла

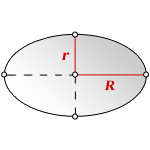
R — большая полуось

r — малая полуось

π ≈ 3.14

Формула площади эллипса, через полуоси:

Калькулятор, вычислить площадь элипса:

1. Формула площади равнобедренной трапеции через стороны и угол

а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, ( S ):

Формула площади равнобедренной трапеции через стороны и угол, ( S ):

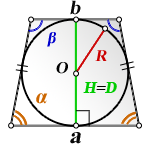
2. Формулы площади равнобедренной трапеции если в нее вписана окружность

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α , β — углы трапеции

а — нижнее основание

b — верхнее основание

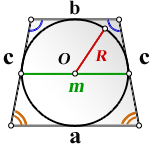
Формула площади равнобедренной трапеции через радиус вписанной окружности, ( S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

R — радиус вписанной окружности

m — средняя линия

O — центр вписанной окружности

c — боковые стороны

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию ( S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α , β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, ( S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c — боковая сторона

m — средняя линия трапеции

α , β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, ( S ):

5. Формула площади равнобедренной трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, ( S ):

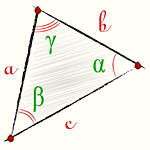
a , b , c — стороны треугольника

α , β , γ — противолежащие углы

Площадь треугольника через сторону и два угла (S):

Формулы для треугольника:

Зная длины всех трех сторон

и используя формулу Герона можно найти площадь разностороннего треугольника

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

Калькулятор — вычислить, найти площадь треугольника:

Формулы для треугольника:

Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
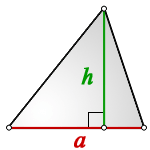
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.

Что бы найти площадь треугольника,

для этого надо основание умножить на высоту и разделить на два

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

1. Площадь разностороннего треугольника

h — высота треугольника

Формула площади треугольника (S):

Калькулятор для расчета площади треугольника

Видео:Площадь треугольника. Формула площади. Геометрия 8 класс.Скачать

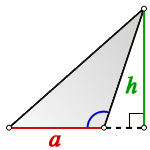
2. Площадь треугольника с тупым углом

h — высота треугольника

Формула площади треугольника с тупым углом (S):

Формулы для треугольника:

Зная у треугольника

две стороны и синус угла между ними, находим по формуле, его площадь

a , b , c — стороны треугольника

α , β , γ — углы

Формулы площади треугольника, через две стороны и угол между ними, (S):

Калькулятор — вычислить, найти площадь треугольника:

Формулы для треугольника:

Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза

1. Если известны только катеты

a , b — катеты треугольника

Формула площади треугольника через катеты ( S ) :

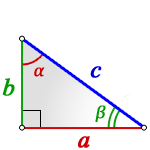
2. Если известны острый угол и гипотенуза или катет

c — гипотенуза

a , b — катеты

α , β — острые углы

Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :

Формулы площади прямоугольного треугольника через катет и угол ( S ) :

Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если

то справедливы следующие тождества:

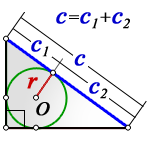
3. Если известны радиус вписанной окружности и гипотенуза

c — гипотенуза

c 1 , c 2 — отрезки полученные делением гипотенузы, точкой касания окружности

r — радиус вписанной окружности

О — центр вписанной окружности

Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :

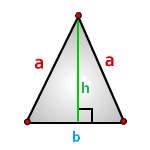
b — основание треугольника

a — равные стороны

h — высота

Формула площади треугольника через высоту h и основание b , (S):

Калькулятор — вычислить, найти площадь треугольника через высоту и основание:

Формула площади треугольника через, стороны a , b , (S):

Калькулятор — вычислить, найти площадь треугольника через равные стороны и основание:

b — основание треугольника

a — равные стороны

h — высота

Формулы для треугольника:

Если вы знаете сторону или высоту

вы можете найти площадь равностороннего треугольника

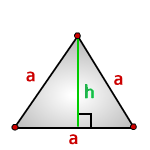
a — сторона треугольника

h — высота

Площадь треугольника через сторону a и высоту h , (S):

Площадь треугольника только через сторону a , (S):

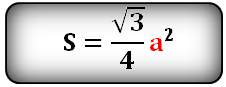
Калькулятор для расчета площади равностороннего треугольника

Площадь треугольника только через высоту h , ( S ):

Калькулятор для расчета площади равностороннего треугольника

a — сторона треугольника

h — высота

Формулы для треугольника:

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Формула площади круга, диаметр

Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса

или радиус круга или длину окружности, можно найти его площадь.

r — радиус круга

D — диаметр круга

Формула площади круга, (S):

на тему: Площадь круга

Калькулятор для расчета площади круга через радиус

Калькулятор для расчета площади круга через диаметр

L — длина окружности

О — центр круга

Формула площади круга если известна длина окружности, (S):

на тему: Площадь круга

Калькулятор для расчета площади круга через длину

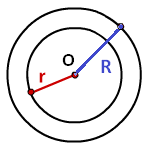
Площадь кольца равна — число π , умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности

R — радиус внешней окружности

r — радиус внутренней окружности

Формула площади кольца (S):

Калькулятор — вычислить, найти площадь кольца

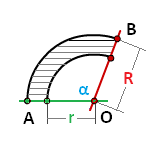
R — радиус внешней окружности

r — радиус внутренней окружности

α — угол сектора AOB, в градусах

Формула площади сектора кольца (S):

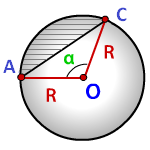
R — радиус круга

α — угол сегмента в градусах

Формула площади сегмента круга (S), отсекаемая хордой AC :

Калькулятор для расчета длины дуги окружности :

Формулы для окружности и круга:

Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол

r — радиус круга

L — длина дуги AB

α — угол сектора круга AOB в градусах

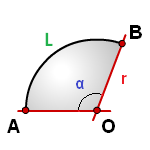
Формула площади сектора круга (S), через длину дуги ( L ):

Формула площади сектора круга (S), через угол ( α ):

Формулы для окружности и круга:

Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

Формулы площади ромба через диагонали и углы между сторонами ( S ):

a — сторона ромба

h — высота

r — радиус вписанной окружности

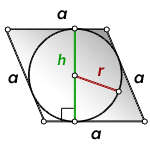
Формула площади ромба через высоту или радиус вписанной окружности ( S ):

1. Формула площади параллелограмма через стороны и углы

a, b — стороны параллелограмма

α , β — углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

Калькулятор — вычислить, найти площадь параллелограмма:

2. Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H _b — высота на сторону b

H _a — высота на сторону a

Формула площади через стороны и высоты параллелограмма, ( S ):

3. Формула площади параллелограмма через диагонали и угол между ними

D — большая диагональ

d —меньшая диагональ

α , β — углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , ( S ):

Калькулятор — вычислить, найти площадь параллелограмма:

Формулы для параллелограмма:

🔍 Видео

Площадь треугольника, построенного на векторахСкачать

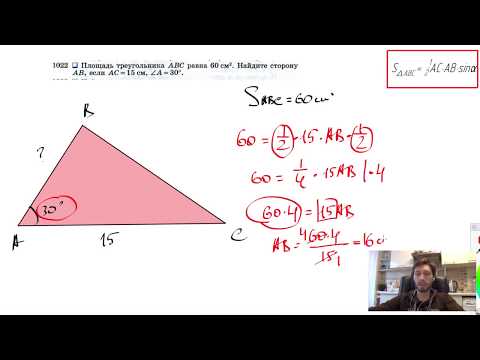
№1022. Площадь треугольника ABC равна 60 см2. Найдите сторону АВ, если АС= 15 см,Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Площадь треугольника, следствиеСкачать

100. Теорема о площади треугольникаСкачать

Геометрия 9 класс : Теорема о площади треугольникаСкачать

Как найти площадь треугольника без формулы?Скачать

Как найти площадь треугольника, зная координаты его вершины.Скачать

✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

ПЛОЩАДЬ ТРЕУГОЛЬНИКА формула 9 класс геометрия АтанасянСкачать

Отношение площадей треугольников с равным угломСкачать