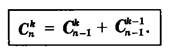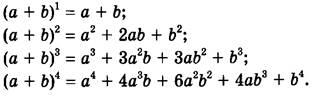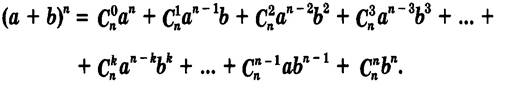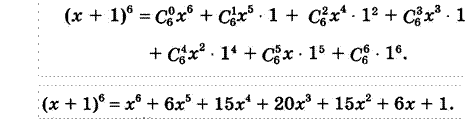План урока треугольник паскаля (4 видео)

Треугольник Паскаля
план-конспект занятия по алгебре по теме

Содержание

Скачать:
Предварительный просмотр:
Конспект на тему «Бином Ньютона. Треугольник Паскаля» (для студентов)
Методическая разработка занятия по теме » Треугольник Паскаля.Бином Ньютона.»
ТЕХНОЛОГИЧЕСКАЯ КАРТА ЗАНЯТИЯ
План занятия
ФОРМИРОВАНИЕ УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙСТВИЙ (ФГОС среднего общего образования) и ОБЩИХ КОМПЕТЕНЦИЙ (ФГОС СПО)
📸 Видео

Видео:Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)Скачать

Скачать:

Вложение	Размер
paskalya.docx	56.81 КБ

Видео:ТРЕУГОЛЬНИК ПАСКАЛЯ 😊 ЧАСТЬ I #shorts #математика #егэ #задачи #задачаналогику #егэ2022 #огэ2022Скачать

Предварительный просмотр:

ВТЖТ – филиал РГУПС

Тема занятия по КТП:

Практическое занятие 56.

1.1. ознакомить студентов с понятием треугольника Паскаля;

1.2. установить зависимость между треугольником Паскаля и формулой бинома Ньютона;

1.3. Сформировать умения и навыки решать задачи на треугольник Паскаля.

2.1. развивать умения пользоваться опорным конспектом и дидактическим материалом для постановки задачи и её выполнения в ходе решения;

2.2. развивать внимательность, собранность и аккуратность, умения работать самостоятельно;

3.1. воспитывать внимание и аккуратность в оформлении заданий.

Раздаточный дидактический материал

Перед началом занятия студент должен знать:

определение перестановок, размещений, сочетаний;
основные формулы комбинаторики;
вычислять факториал;
формулу бинома Ньютона;
свойства биномиальных коэффициентов.

По окончании занятия студент должен уметь:

Строить треугольник Паскаля, пользоваться ими при разложении бинома Ньютона.

1. Организационный этап (5 мин). Сообщение темы и целей занятия.

2. Проверка домашнего задания (разбор нерешенных задач). (10 мин).

3. Актуализация опорных знаний (10 мин).

Вычислить , .
Разложить в многочлен: .

4. Практическая работа (40 мин).

На прошлом занятии мы заметили, насколько рационализируется работа по возведению двучлена в степень, если использовать бином Ньютона. Но на самом деле нашу работу можно ещё упростить. Достаточно долго мы вычисляли биномиальные коэффициенты, а коэффициенты – это сочетания. Посмотрите внимательно, все ли свойства сочетаний, которые были ранее введены, мы использовали?

Свойство осталось не востребованным, именно его используют при построении треугольника Паскаля .

Определение: Треугольник Паскаля — это треугольник, составленный из чисел, являющихся коэффициентами в формуле бином Ньютона.

Каждый крайний элемент равен 1, а каждый не крайний элемент равен сумме двух своих верхних соседей.

Треугольник можно продолжать до бесконечности, но на практике чаще составляют таблицу для первых 10 степеней.

Видео:Треугольник ПаскаляСкачать

Конспект на тему «Бином Ньютона. Треугольник Паскаля» (для студентов)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Формула бинома Ньютона. Треугольник Паскаля

Мы познакомимся с формулой бинома Ньютона. Выясним, что эта формула согласуется с формулами квадрата и куба суммы и разности. Рассмотрим, как использовать формулу бинома Ньютона при увеличении показателя степени , выясним, какое отношение имеет треугольник Паскаля к биному Ньютона. Рассмотрим примеры, с использованием бинома Ньютона и треугольника Паскаля.

Бином Ньютона — формула разложения произвольной натуральной степени двучлена в многочлен. Каждый из нас изучал наизусть формулы «квадрата суммы» и «куба суммы» , но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности.

Чтобы не совершить ошибку и применяется формула бинома Ньютона и треугольник Паскаля.

Формула бинома Ньютона для натуральных n имеет вид:

где числа – называют биномиальными коэффициентами.

– формула для числа сочетаний, .

К примеру, известная формула сокращенного умножения «квадрат суммы» вида:

есть частный случай бинома Ньютона при n=2.

Выражение, которое находится в правой части формулы бинома Ньютона, называют разложением выражения

Запомнить формулу действительно непросто. Но попытаемся её проанализировать.

Видно, что в любом многочлене присутствуют и с коэффициентами 1. Ясно также, что всякий иной член многочлена выглядит как произведение определённых степеней каждого из слагаемых двучлена ), причём сумма степеней всегда равна n.

Например, в выражении сумма степеней сомножителей во всех членах равна трём (3, 2+1, 1+2, 3). То же самое справедливо и для любой другой степени. Вопрос лишь в том, какие коэффициенты следует ставить при членах.

Видимо, для того чтобы облегчить труд обучающихся, великий французский математик и физик Блез Паскаль триста пятьдесят лет назад придумал специальный инструмент для определения этих самых коэффициентов — «треугольник Паскаля»

Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля.

В общем виде треугольник Паскаля имеет следующий вид:

Видео:Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

Методическая разработка занятия по теме » Треугольник Паскаля.Бином Ньютона.»

Методическая разработка занятия, разработана Л.П.Утевой, преподавателем математики. Тема методической разработки – «Треугольник Паскаля Формула бинома Ньютона». Данное занятие относится к блоку «Комбинаторика, статистика и теория вероятностей», разделу «Комбинаторика».

В соответствии с новыми стандартами процесс учения понимается не только как усвоение системы знаний, умений и навыков, составляющих инструментальную основу компетенций учащегося, но и как процесс развития личности, обретения духовнонравственного опыта и социальной компетентности. В основе разработки стандартов нового поколения лежит системно-деятельностный подход, который позволяет выделить основные результаты обучения и воспитания и создать навигацию проектирования универсальных учебных действий, которыми должны владеть учащиеся. Логика развития универсальных учебных действий, помогающая ученику почти в буквальном смысле объять необъятное, строится по формуле: от действия – к мысли. Овладение учащимися универсальными учебными действиями создаёт возможность самостоятельного успешного усвоения новых знаний, умений и компетентностей, включая организацию усвоения, т.е. умения учиться.

В основе занятия лежит системно-деятельностный и компетентностный подходы к обучению, согласно которым учащиеся овладевают умением формулировать и анализировать факты, работать с различными источниками, выдвигать гипотезы, осуществлять доказательства правильности гипотез, формулировать выводы, отстаивать свою точку зрения при обсуждении учебной деятельности, что формирует нравственные качества личности. Базовыми понятиями данного подхода являются: воспитание и развитие качеств личности, соответствующих требованиям современности, коими являются гражданственность, универсальность познавательных действий, социальность, индивидуализация. Достижение результата важно через включение в деятельность.

Эффективными приемами, способствующими социализации личности, на данном занятии являются аналитическая беседа, создание ситуаций успеха, активные методы обучения («Шаг на встречу») и тд.

Тема по математике «Треугольник Паскаля. Формула бинома Ньютона». представляет собой занятие по изучению нового материала с применением мультимедиа технологий и призвана продолжать формирование всех универсальных учебных действий и общих компетенций:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

В соответствии с намеченными целями изучения темы и требованиями Федеральных государственных образовательных стандартов как среднего общего, так и среднего профессионального образования, структура занятия включает в себя следующие этапы:

1. Организационный этап.

2. Постановка цели и задач занятия. Мотивация учебной деятельности студентов.

3. Актуализация знаний, УУД, ОК.

4. Первичное усвоение новых знаний, УУД, ОК.

5. Первичная проверка понимания материала.

6. Первичное закрепление новых знаний, УУД, ОК.

7. Информация о домашнем задании.

При проведении данного занятия используются элементы современных педагогических технологий (личностно-ориентированного, проблемного обучений, информационно — коммуникационной технологий). Занятие мотивирует к дальнейшему самостоятельному изучению дисциплины, повышает уровень организованности студентов и учит работать в коллективе.

Методическая разработка данного занятия и разработанные преподавателем материалы – презентация, технологическая карта могут быть использованы для проведения занятий по дисциплине «Математика: алгебра, начала математического анализа, геометрия» у студентов I курса всех специальностей в учреждениях среднего и начального профессионального образования.

Видео:Математические секреты треугольника ПаскаляСкачать

ТЕХНОЛОГИЧЕСКАЯ КАРТА ЗАНЯТИЯ

ПРЕПОДАВАТЕЛЬ: Утева Л.П.

ТИП УРОКА: занятие по изучению нового материала.

ВИД УРОКА: смешанное занятие.

ДИСЦИПЛИНА: ОУДП. 04 Математика: алгебра, начала математического анализа, геометрия ТЕМА ЗАНЯТИЯ: «Треугольник Паскаля Формула бинома Ньютона».

МЕТОДИЧСЕКАЯ ЦЕЛЬ: показать на учебном занятии применение продуктивных методов обучения (групповая работа, активные методы, использование ИКТ) ЦЕЛИ ЗАНЯТИЯ:

• формирование комбинаторного мышления через решение задач;

• ознакомление с треугольником Паскаля и биномом Ньютона и установление взаимосвязей между ними;

• развитие умение анализировать и обобщать полученные знания;

• развитие познавательного интереса, и культуры математической речи;

• способствовать развитию кругозора, памяти, мышления, наблюдательности,

пространственного представления и пространственного воображения;

• формировать чувство ответственности, самостоятельности, аккуратности, оперативности; • формировать познавательные потребности, дисциплинированность, умение работать в коллективе.

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ: личностные:

понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;

развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и

овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественнонаучных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;

готовность и способность к самостоятельной творческой и ответственной деятельности;

умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения;

целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;

сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;

сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

МЕТОДЫ ОБУЧЕНИЯ: проблемный, активные методы, объяснительно-иллюстративный, видеообучение

ПЕДАГОГИЧЕСКИЕ ТЕХНОЛОГИИ: информационно-коммуникативные, технология развития критического мышления.

ФОРМЫ ОРГАНИЗАЦИИ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ: фронтальная

(коллективная), парная, групповая, индивидуальная.

• Мультимедийный проектор, ПК, звуковые колонки, презентация.

1. Мордкович. А.Г. Алгебра и начала математического анализа. 10-11кл. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. – 14-е изд., стер. М.: «Мнемозина», 2013. – 400с.

2. https://www.youtube.com/watch?v=6TXH5pwPRH8 — видеоролик о треугольнике Паскаля

Видео:Числа сочетаний. Треугольник Паскаля | Ботай со мной #059 | Борис Трушин |Скачать

План занятия

1. Организационный этап.

2. Постановка цели и задач занятия. Мотивация учебной деятельности студентов. • активный метод «Шаг навстречу»

• формулировка темы, целей.

3. Актуализация знаний, УУД, ОК.

• Интерактивное задание на проверку знаний определения и формул перестановок, сочетаний и размещений; • упражнение на решение комбинаторных задач;

4. Первичное усвоение новых знаний, УУД, ОК.

• вывод свойства сочетаний;

• вычисление сочетаний и построение треугольника Паскаля;

5. Первичная проверка понимания материала.

• решение примера на применение бинома Ньютона;

6. Первичное закрепление новых знаний, УУД, ОК.

• просмотр видеоролика; 7. Информация о домашнем задании.

Организационный этап. Преподаватель приветствует учащихся, задает настрой, проверяет список присутствующих.

Постановка цели и задач занятия. Мотивация учебной деятельности студентов.

На экране появляется слайд с надписями: сочетания, размещения, коэффициенты, многочлен, треугольник Паскаля, бином, n!, 0!, 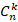, (a+b) n , (a+b) 2 . Преподаватель предлагает учащимся обсудить, какие термины и формулы им знакомы, а какие нет (активный метод «Шаг навстречу»). Основываясь на обсуждении, преподаватель совместно с учащимися формулирует тему занятия. Учащиеся записывают свои цели, опасения и ожидания.

Актуализация знаний, УУД, ОК.

Учащиеся выполняют интерактивное задание на платформе https://coreapp.ai , и задачи по вариантам на слайде , взаимоконтоль в парах.

Первичное усвоение новых знаний, УУД, ОК.

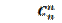
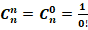
Преподаватель предлагает студентам вычислить сочетания , что приводит к формуле . Возникает вопрос, чему равен 0! (Коллизия). Учащиеся обсуждают этот вопрос, преподаватель помогает им прийти к мысли о том, что n элементов из множества n элементов можно выбрать одним способом. Аналогично 0 элементов из n можно выбрать одним способом – ничего не выбирая. Учащиеся приходят к выводу, что 0!=1.

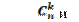
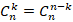
Затем учащимся предлагается вычислить , что приводит их к свойству

.Учащиеся в парах обсуждают в каких случаях, задачах будет полезна эта

Преподаватель предлагает учащимся посчитать, сколькими способами можно выбирать элементы из множества 1, 2, 3, 4,5 элементов с помощью сочетаний, при этом учащиеся используют полученное свойство.

Учащиеся получают треугольник Паскаля и совместно с преподавателем обсуждают его особенности и свойства.

Учащиеся замечают, что по краям треугольника стоят единицы, а остальные элементы каждой строки получаются путем сложения двух вышестоящих элементов, что приводит к ещё одному свойству сочетаний (биномиальных коэффициентов).

Преподаватель говорит учащимся о том, что треугольник хранит в себе ещё много тайн и загадок, с некоторыми из которых они познакомятся на занятии, а некоторые могут изучить самостоятельно.

Преподаватель задаёт учащимся раскрыть скобки в формулах

Учащиеся работают в группах, проверяют друг друга по формулам, изображенным на слайде, и обсуждают полученные результаты.

Они замечают взаимосвязь между треугольником Паскаля и коэффициентами в формулах. Преподаватель записывает общую формулу и объясняет учащимся, что эта формула называется формулой бинома Ньютона и, используя треугольник Паскаля, можно раскрыть скобки с любой степенью. Бином – это двучлен (по аналогии с многочленом). Сочетания в формуле бинома называются биномиальными коэффициентами и свойства сочетаний – это и есть свойства биномиальных коэффициентов.

Первичная проверка понимания материала.

Совместно с преподавателем учащиеся разбирают пример на применение полученной формулы, обсуждают результаты.

Первичное закрепление новых знаний, УУД, ОК.

Учащиеся смотрят видеоролик о треугольники Паскаля, его свойствах и применении, обсуждают его.

Информация о домашнем задании.

Преподаватель говорит учащимся о том, что у треугольника Паскаля ещё множество удивительных свойств и они могут найти об этом информацию и подготовить доклады.

Студенты оценивают свой уровень достижения целей урока.

Видео:Треугольник ПаскаляСкачать