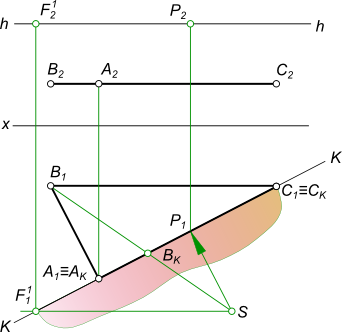
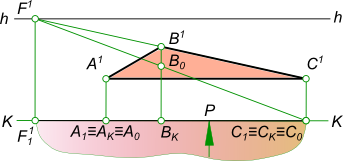
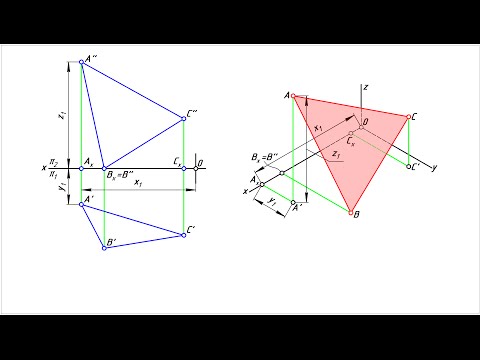
Перспектива треугольника в черчении

Перспектива плоскости треугольника ABC может быть построена если заданы ее ортогональные проекции.

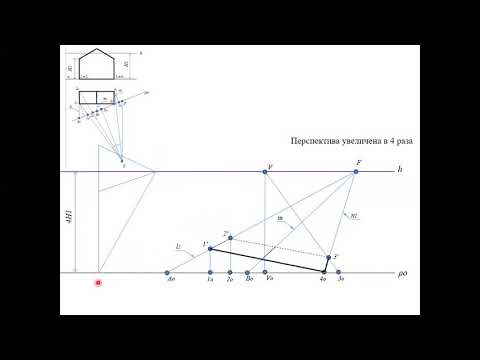
Перспектива плоскости треугольника ABC может быть построена, если будет обеспечено последовательное выполнение следующих действий:

— выбор положения следа картинной плоскости. Плоскость картины совпадает с стороной AC; — выбор положения точки зрения S выполняем так, чтобы главный луч зрения SP, перпендикулярный картинной плоскости, проходя через нее, делил перспективное изображение плоскости треугольника примерно пополам; — в дополнение к точкам A_KC_K строим точку B_K, проводя луч SB₁; — строим перспективное изображение A 1 C 1 стороны AC; — параллельно B₁C₁ проводим вспомогательный луч из точки S и находим точку схода стороны BC; — точку схода стороны BC переносим на с основания картинной плоскости на заданную линию горизонта в точку F 1 ; — из точки F 1 проводим прямые F 1 C 1 и F 1 C₀; — в пересечении перпендикуляра к основанию картины в точке B K с прямыми F 1 C 1 и F 1 C₀ находим точки B 1 и B 0 ; — соединяем прямой линией точки A 1 B 1 , замыкая контур треугольника. Таким образом, получена перспектива плоскости треугольника ABC.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Построение перспективы «методом архитекторов».

В основе «метода архитекторов» лежит построение перспективы заданного объекта по плану и фасаду с учётом положения точки зрения. В этом построении используют «способа канонического сечения» (план) и точки схода доминирующих направлений объекта (одна или две).

Положение вертикальных рёбер объекта определяют, проведя проектирующие лучи из точки стояния в точки вертикальных рёбер плана. Затем их переносят на картинув соответствующем масштабе. Высоты определяют с помощью перспективных масштабов высот, путём их приближения до совпадения с картиной, где ребро будет отображаться в натуральную величину перспективного масштаба.

Перспективное изображение зависит от положения картинной плоскости, точки зрения и высоты горизонта.

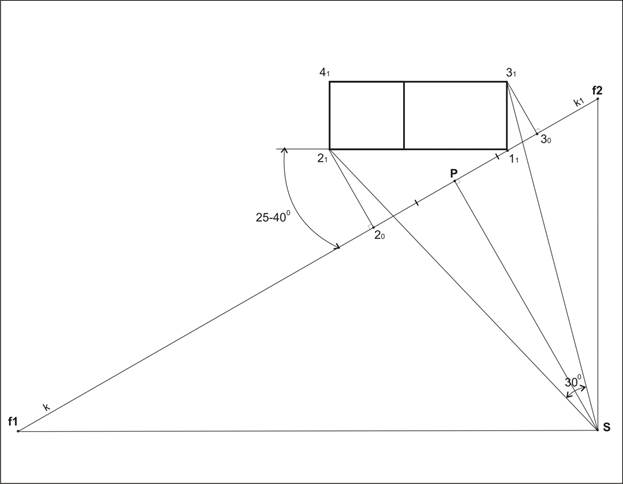
На плане картинную плоскость задают её основанием как проецирующую плоскость. Положение картинной плоскостина плане объекта выбирают так, чтобы перспектива верно отражала пропорции изображаемого объекта. Её лучше всего проводить через угол заданного объекта под углом 25 0 — 40 0

Точка зрения задаётся на чертеже объекта. В начале определяем положение главного луча зрения и отмечаем главную точку схода картины Р – место пересечения главного луча с картинной плоскостью. Как правило, главныйлуч зрения проходит через середину объекта. Для нахождения тоски Р из крайних точек объекта накартинную плоскостьопускают два перпендикуляра и расстояние между ними делит пополам и отмечает центральную точку схода Р. Из неё проводят центральный луч зрения под прямым углом к картинной плоскости.

Затем определяют расстояние от точкизрения до объекта. Необходимо чтобы объект полностью попадал в поле (конус) ясного зрения. Оптимальный угол зрения должен быть равен 28 0 — 30 0 . Для нахождения точки зрения S можно взять треугольник с одним из углов в 30 0 и, положив его вершину на главный луч зрения, двигать треугольник по лучу до тех пор, пока крайние грани ни совпадут с крайними точками объекта. Вершина отметит положение точки зренияS.

Положение точкиSможно найти графическим способом. На основании картинной плоскостипроизвольно отмечаем точкуР0 и восстанавливаем из нё перпендикуляр. Слева и справа от точкиР0на произвольно заданном одинаковом расстоянии на основании картинной плоскости откладываем точки А0 и В0. Три – четыре длинны отрезка А0В0 откладываем на перпендикуляре от точкиР0. Отмечаем точку S0. Соединяем точкуS0 с точкамиА0 и В0 . Из крайних точек объекта проводим прямые параллельные S0А0и S0В0. Их пересечение определяет точку зрения S.

Высоту горизонта принимают исходя из размеров объекта и назначения перспективы. Если горизонт высокий, то построение плана в перспективе упрощается.

На основании картины определяем точки f1 и f2.Для их нахождения из точки зренияпроводим две прямые параллельно доминирующим направляющим сторон плана объекта (горизонтальные и вертикальные). Эти прямые, пересекаясь с основаниемкартинной плоскости, отмечают искомые точкиf1 и f2.

Построение перспективы «методом архитекторов» (1).

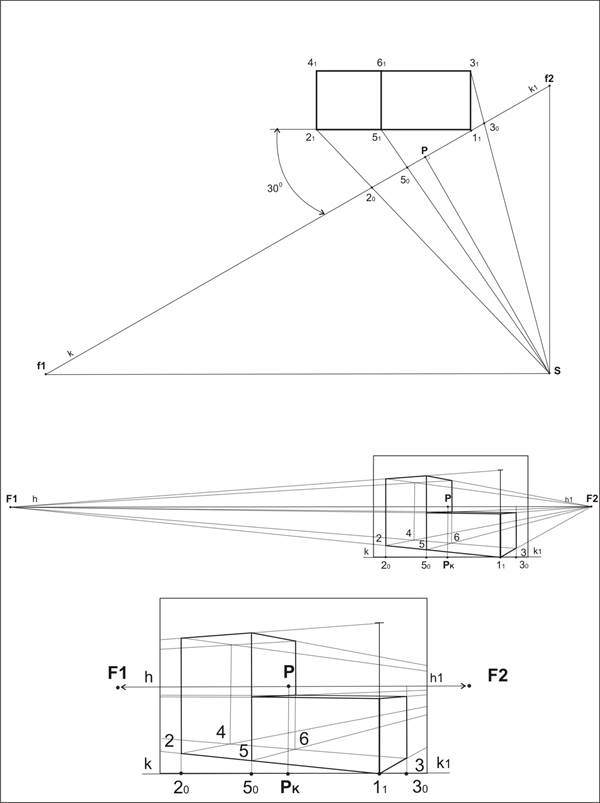
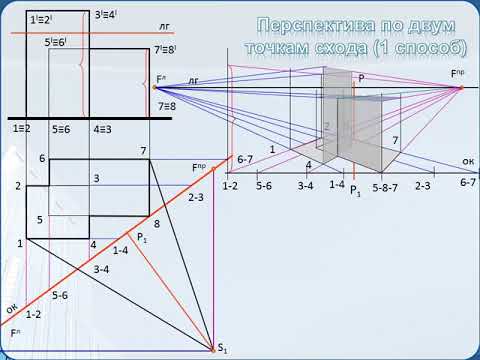
Переходим к построению перспективы объекта с двумя точками схода. На плане из точки зренияSпроводим прямые ко всем видимым вершинам объекта и отмечаем их пересечение с основанием картины 10,20,30. Ребро 11 совпадает с картиной и остается без изменений (проектируется в натуральную величину). Справа от чертежа или на отдельном листе бумаги проводим основание картинной плоскости и отмечаем на ней точку схода Р. Задаём положение линии горизонта. На неё с основания картинной плоскости переносят, с помощью вертикальных линий, главную точку схода Р, точки схода F1иF2 и точки 10,20,30.… Из точки 11 проводим прямые в точки сходаF1иF2 , которые в пересечении с вертикалями, проведёнными из вершин объекта, дают перспективу рёбер 2,3,5.

Построение перспективы «методом архитекторов» (2).

Из точек 2 и 5проводим прямые линии в F2,из точки 3 в F1 и заканчиваем построение перспективы плана объекта.

Для построения высот объекта, в рассматриваемом примере, можно использовать ребро 1. На нём откладывают натуральные величины и из этих отметок проводят прямые в точку F1.Пересекая рёбра 2 и 5, они отмечают искомые высоты.. Используя точку схода F2,достраиваем перспективу объекта.

Видео:ТЕМА 1. ОСНОВЫ ПЕРСПЕКТИВЫСкачать

Урок 3. Линейная перспектива. Построения, часть 1.

Без знания законов линейной перспективы невозможно реалистично изобразить ни один объемный предмет, будь то человек или табуретка.

Но пугаться не стоит. Несмотря на громкое название, основных законов всего два и запомнить их очень просто.

Все вы когда-нибудь ездили на электричке и переходя железнодорожные пути, смотрели не идет ли поезд. Что вы видели в этот момент?

Сходящие на линии горизонта рельсы, очевидно, параллельные друг другу.

И одинаковой высоты столбы линии электропередач, ближний из которых кажется значительно больше дальнего.

Собственно, это и есть два основных закона линейной перспективы:

1. Параллельные прямые, удаляющиеся от нас мы видим сходящимися в одной точке. Эта точка называется точкой схода. Она, или ее проекция находится на линии горизонта
2. Предметы одинаковой величины кажутся тем меньше, чем дальше от нас они расположены.

Видео:Перспектива. Метод архитекторовСкачать

Основные понятия перспективы.

Перед тем, как мы начнем применять эти законы на практике, я дам вам несколько определений. Это упростит объяснения и поможет вам легче понимать специальную литературу.

Горизонт ( линия горизонта) — плоскость, горизонтальная, бесконечная, находящаяся на высоте глаз наблюдателя и ВСЕГДА видимая в виде прямой горизонтальной линии.

Условно можно считать, что перспективный горизонт и горизонт географический в нашем зрении совпадают.

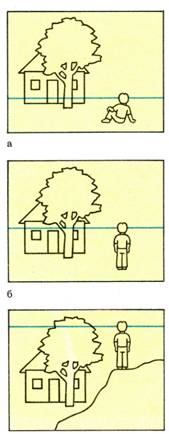
Все предметы, находящиеся ниже этой плоскости, ниже горизонта, мы видим сверху; все предметы, находящиеся выше горизонта,- видим снизу.

Важно запомнить, что линия горизонта всегда находится на уровне ваших глаз. Если вы сядете на землю, то перспективный горизонт опустится вместе с вами, при подъеме в гору он поднимается.

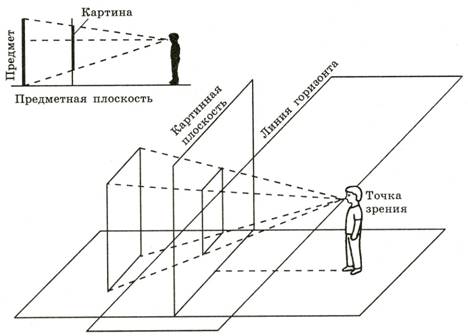
Точка зрения – условное расположение взгляда художника относительно изображаемого объекта.

Картинная плоскость — условная плоскость, на которую проецируется изображение. Она всегда вертикальна. Независимо от того, как расположен ваш лист.

Сокращения. Если поверхность находится под углом к картинной плоскости, она нам кажется более узкой, чем когда она параллельна картинной плоскости. Этот эффект называется — сокращения. Чем ближе угол между плоскостями к 90 градусам, тем больше сокращения. Если угол равен 90 градусам, мы видим поверхность, как линию.

Видео:Метод Архитекторов с одной точкой схода. Семестровая работаСкачать

Основные понятия. Тест.

Чтобы закрепить полученные знания, предлагаю вам пройти небольшой тест. Ответы присылайте, пожалуйста, мне в личном сообщении.

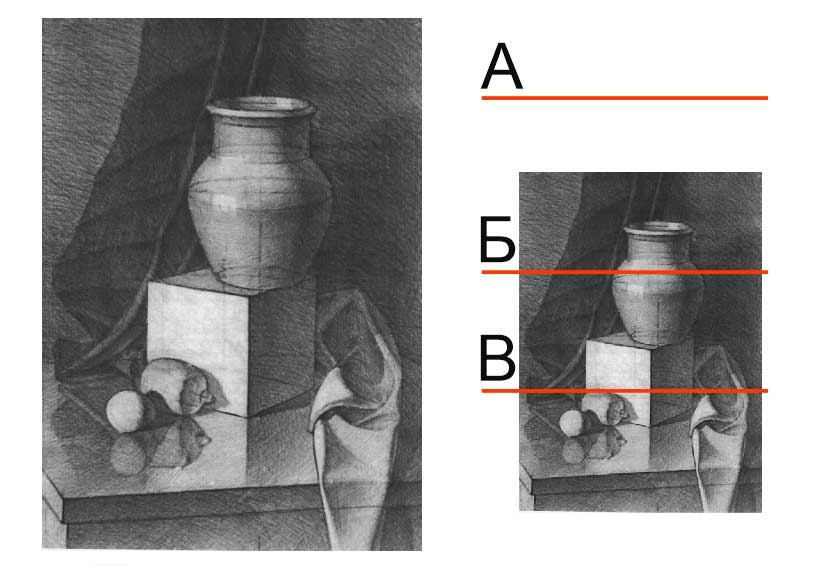
1. Где находится линия горизонта на картине.
   1. А
   2. Б
   3. В
   4. В натюрморте ее нет, горизонт виден только в пейзаже.
2. Картинная плоскость…
   1. … всегда совпадает с плоскостью листа, на котором вы работаете.
   2. … может совпадать, если лист расположен вертикально и прямо перед вами.
   3. … никогда не совпадает.
3. Геометрические тела в натюрморте находятся …
   1. … на линии горизонта.
   2. … выше линии горизонта.
   3. … ниже линии горизонта.
   4. … и выше и ниже.

Видео:Построение равностронего треугольника.Скачать

Перспектива с одной точкой схода.

Один из двух наиболее распространенных типов перспективных построений. Мы ее используем, когда рисуем объект с прямыми углами, передняя сторона которого параллельна картинной плоскости. Этот тип построений часто используется для изображений интерьеров и архитектуры.

Saint Jerome in His Study Albrecht Dürer 1514

Видео:Построение треугольника в трёх проекцияхСкачать

Разберем построения перспективы с одной точкой схода на примере построения куба.

• Нарисуем на нашем листе линию горизонта. Местоположение выбираем произвольно, лучше в середине или верхней трети листаю
• Нарисуем переднюю сторону куба, ниже линии горизонта.Она будет видна нам без искажений, то есть как квадрат.

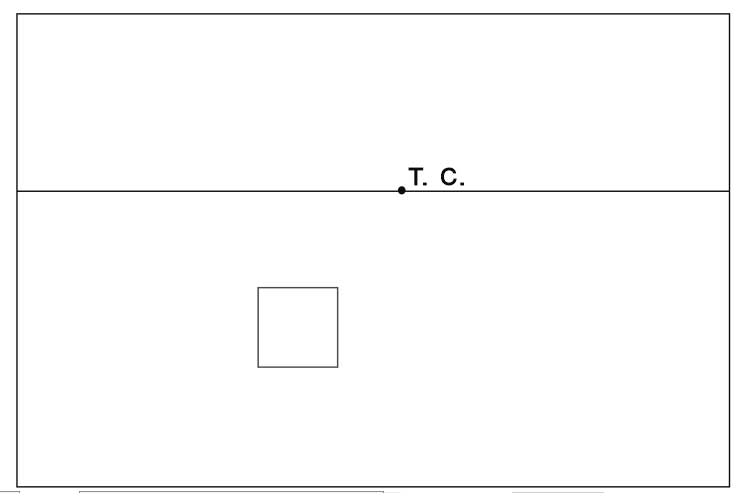
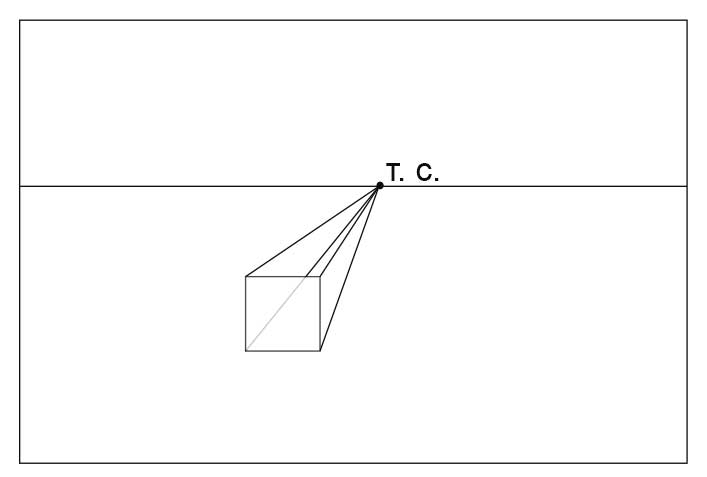
• Зададим точку схода (Т.С.) на линии горизонта. Когда мы рисуем по воображению, мы ее задаем произвольно. При натурном рисовании, она зависит от нашей точки зрения и определяется по параллельным прямым в изображаемом объекте.

• Уходящие от нас ребра куба параллельны друг другу, а значит сходятся на линии горизонта в точке схода. Проведем прямые из углов передней стороны куба в точку схода.

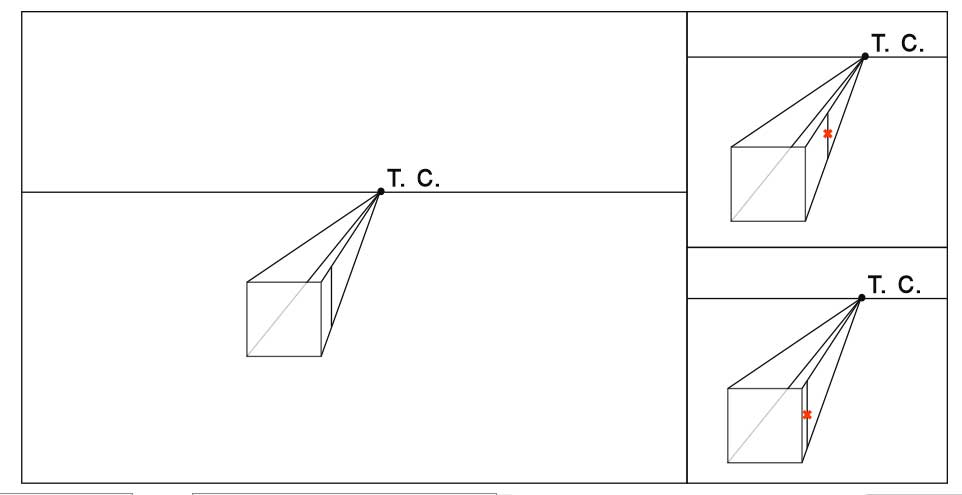
• Определим на глаз длину уходящих от нас ребер куба. Мы видим их в сокращении. Справа от рисунка показаны ошибка при определении длины.

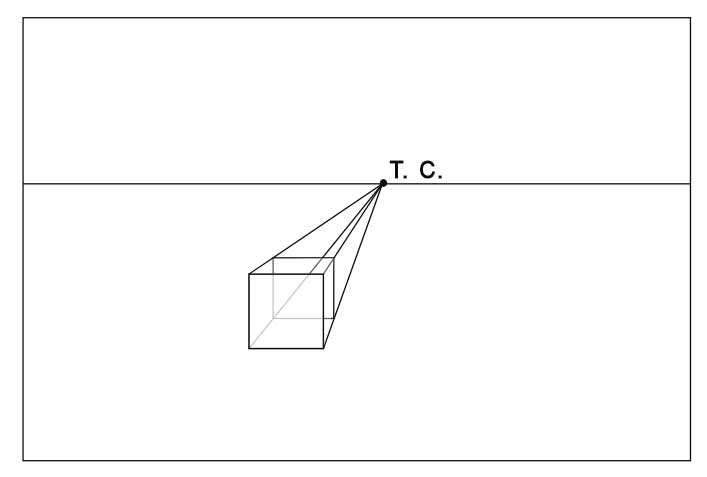
• Достраиваем дальнюю сторону куба. Обратите внимание, что она тоже видна нам без искажений, то есть, как квадрат.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Упражнение 1.

Постройте кубы на линии горизонта и выше нее.

Видео:Лекция 7. Перспектива. Часть 1.Скачать

Дополнительное упражнение 1.

Распечатайте работы, восстановите построение и найдите, где проходит линия горизонта.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

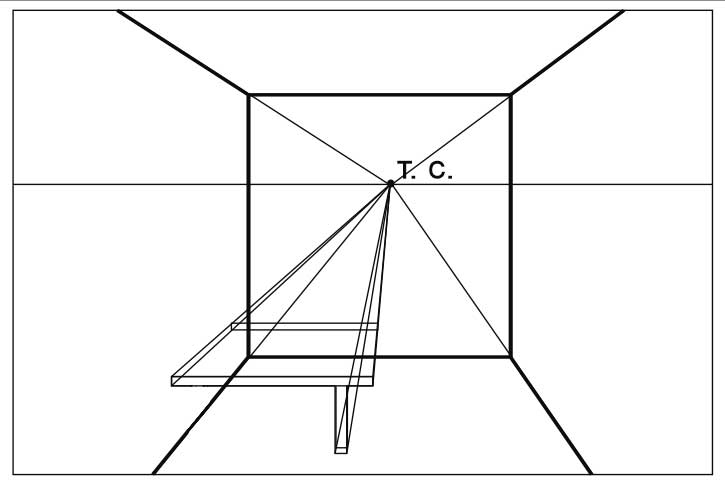
Дополнительное упражнение 2.

Постройте недостающие ножки у стола.

Видео:Построение перспективыСкачать

Перспектива с двумя точками схода.

Это более распространенный тип перспективных построений. Мы им пользуемся тогда, когда изображаем объекты, стороны которых расположены под прямым углом друг к другу. Сами эти объекты могут находиться под произвольными углом к картинной плоскости.

Обратите внимание, что несмотря на название типа построения, на одной работе точек схода может быть бесконечно много. Потому что для каждой группы параллельных прямых точка схода своя. Если у вас на работе несколько предметов, расположенных под разным углом к картинной плоскости, групп параллельных прямых тоже будет несколько.

View of Warsaw from the Terrace of the Royal Castle
Bernardo Bellotto1773

В одной работе могут совмещаться построение перспективы с одной и с двумя точками схода.

В системах построения с одной и с двумя точками схода мы условно считаем все вертикали строго вертикальны. Мы не учитываем, что вы смотрите на объект сверху или снизу и, соответственно, один из его краев ближе к вам, а вертикальные грани являются параллельными прямыми, удаляющимся от вас и должны иметь точку схода. Если вы хотите учитывать этот фактор, вам нужно использовать систему построения с тремя точками схода. Но о ней и о других системах построения объемных изображений мы будем говорить в следующем курсе.

Видео:Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

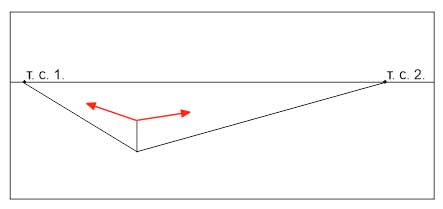
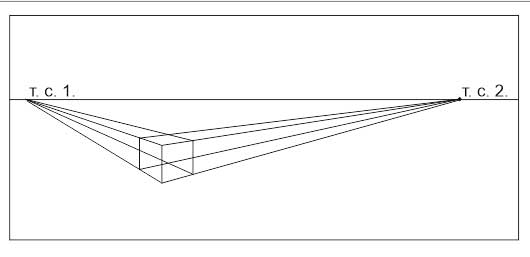
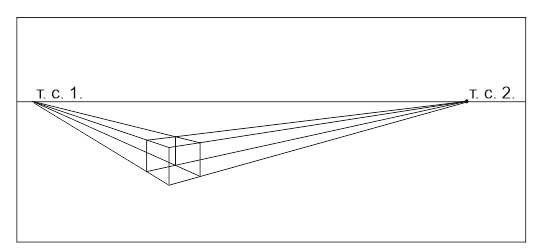
Разберем построения перспективы с двумя точками схода на примере куба.

• Проводим линию горизонта по центру листа или чуть выше.
• Произвольно задаем длину переднего вертикального ребра куба.

• Задаем направления горизонтальных, уходящих от нас, ребер куба. Углы выбираем произвольно, но стараемся, чтобы визуально угол между ребрами читался как прямой. (Он не будет прямым в геометрическом смысле, так как он находится не в плоскости, параллельной картинной, и мы видели его с перспективными искажениями)

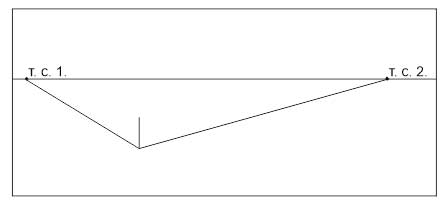
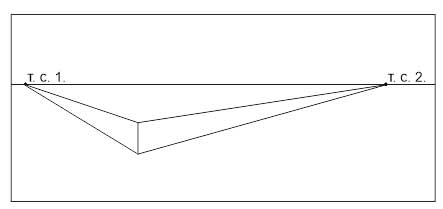
• Продлеваем горизонтальные ребра до линии горизонта. На пересечении получаем две точки схода (Т.С1 и Т.С.2).

• От верхнего края переднего ребра проводим линии в точки схода.

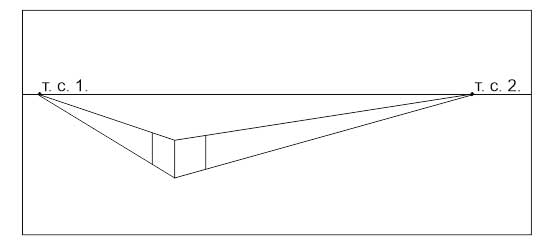
• На глаз определяем ширину боковых сторон куба. Обратите внимание, что их ширина будет меньше высоты, так как мы видим ее в сокращении, а высоту- нет. Чем на вашем рисунке меньше угол между горизонтальным и вертикальным ребром, тем уже соответствующая сторона.

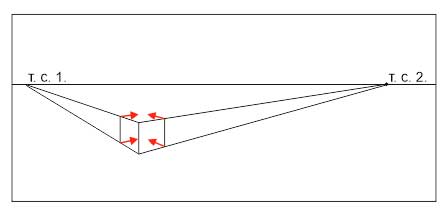
• От дальних углов боковых поверхностей проводим линии в точки схода.

• На пересечении получаем верх и низ дальнего вертикального ребра. Соединяем их — строем ребро.

Видео:Шестиугольник в изометрииСкачать

Упражнение 2.

Постройте кубы на и выше линии горизонта с теми же точками схода.

Видео:Изометрическая проекция треугольникаСкачать

Задание. Воображаемый интерьер.

То, что окружает человека иногда говорит о нем больше, чем его внешность. Мне бы хотелось, чтобы вы придумали интерьер «с характером»: пространство, глядя на которое понимаешь, кто там обитает или что там произошло. Хотя ни обитателей ни событий мы не видим.

Как примеры тем предлагаю:

» комната, где прячется преступник»

«комната одинокого человека»

«комната, где находят ответы на вопросы»

Если вы боитесь не справиться с интерьером, можно взять упрощённый вариант задания — предмет мебели, по которому можно узнать владельца, Например: » любимое кресло старого профессора». Можно пофантазировать на тему любимых предметов мебели литературных героев.

Видео:Уроки рисования. Как рисовать перспективу. Линейная перспектива. Учимся перспективе за 15 минут.Скачать

Дополнительное упражнение 3.

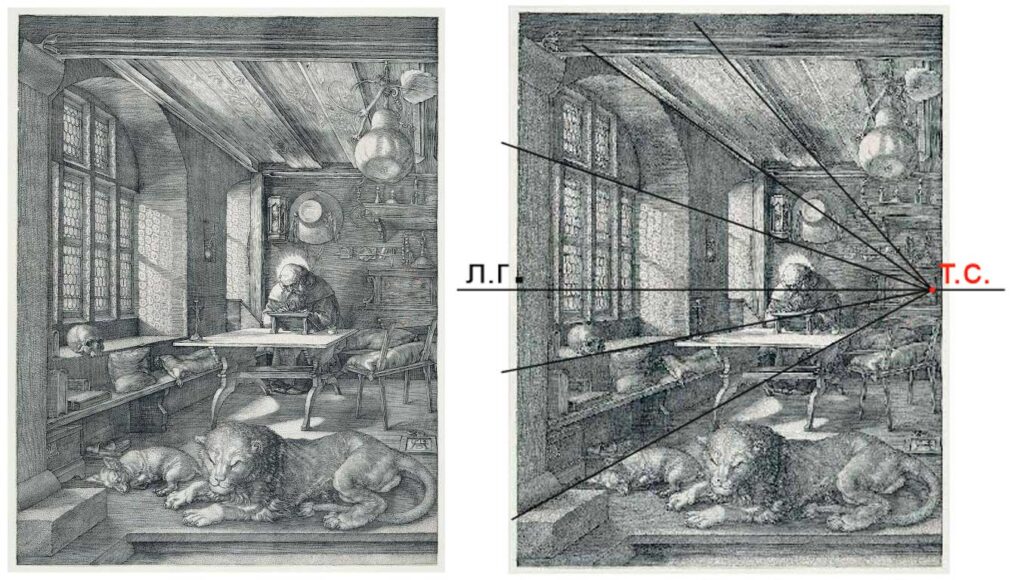
Даже мастера путались в построениях.

Распечатайте картины, восстановите линии построения и найдите, где ошиблись художники.

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Дополнительное задание.

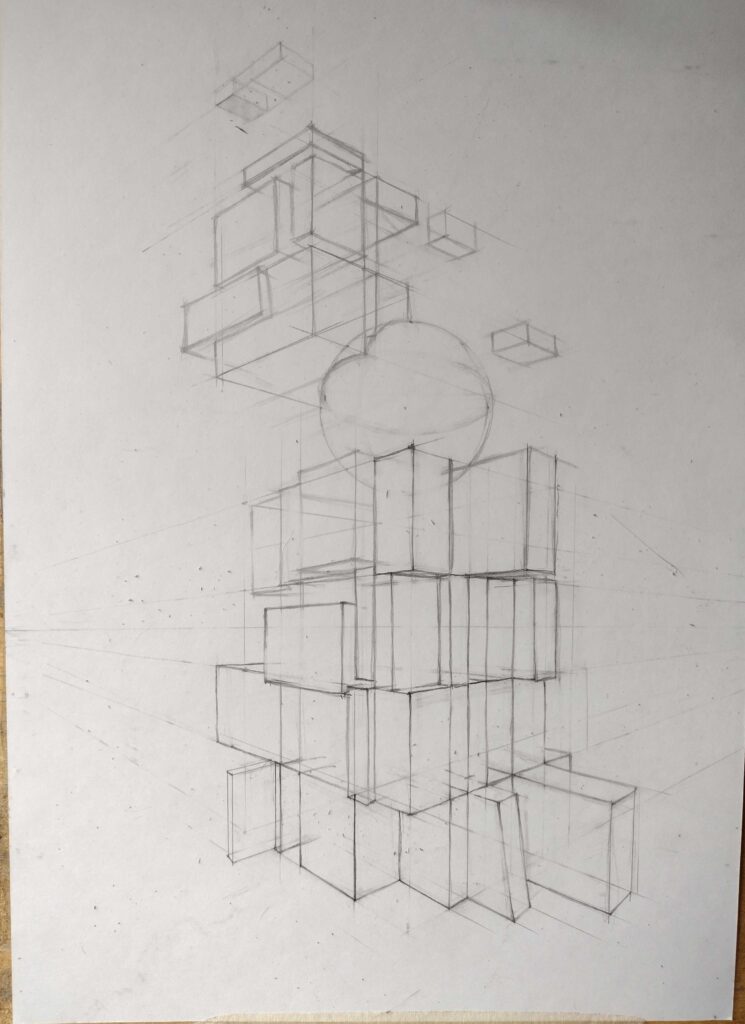
Композиция из геометрических тел. Линейный рисунок без тона. Основные элементы строим напросвет( так, как будто они из стекла) Стараемся пока использовать только кубы или прямоугольные параллелепипеды.

Кубы построены напросвет

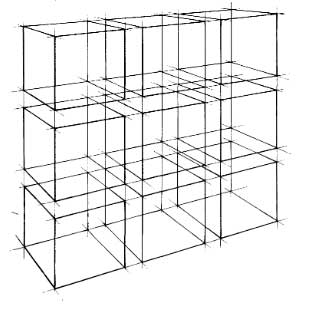
Предлагаю вам вообразить себя архитектором или скульптором-абстракционистом и придумать интересную и эстетичную конструкцию из геометрических тел. Вы можете создать просто гармоничную структуру или попробовать изобразить абстрактное понятие, например, тяжесть или легкость, величие, власть или угрозу. Любые, даже самые необычные варианты, приветствуются.

📽️ Видео

Лекция 7. Перспектива. Часть 2.Скачать

Лекция 7. Перспектива. Часть 3.Скачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

Черчение. 8 класс. Мазаева И.М. Изометрия и ДиметрияСкачать