Контрольные задания по теме: Рабочая тетрадь задача 44, задача 45
Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.
Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.
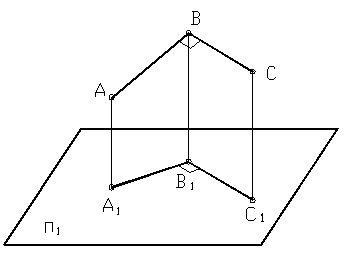
Рисунок 28
Сторона ВС прямого угла АВС, изображенного на рисунке 28, параллельна плоскости П 1 . Следовательно, проекция угла АВС на эту плоскость будет представлять прямой угол А 1 В 1 С 1 =90.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. При построении перпендикуляра из множества прямых принадлежащих плоскости, выбирают прямые уровня — горизонталь и фронталь. В этом случае горизонтальную проекцию перпендикуляра проводят перпендикулярно горизонтали, а фронтальную -перпендикулярно фронтали. На примере, изображенном на рисунке 29, показано построение перпендикуляра к плоскости, заданной треугольником АВС, из точки К. Для этого сначала проводим горизонталь и фронталь в плоскости. Затем из фронтальной проекции точки К проводим перпендикуляр к фронтальной проекции фронтали, а из горизонтальной проекции точки – перпендикуляр к горизонтальной проекции горизонтали. Затем строим точку пересечения данного перпендикуляра с плоскостью при помощи вспомогательной секущей плоскости Σ. Искомая точка – F. Таким образом, полученный отрезок КF является перпендикуляром к плоскости АВС.
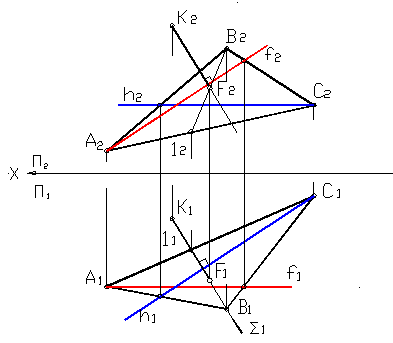
Рисунок 29
На рисунке 29 изображено построение перпендикуляра КF к плоскости АВС.
Две плоскости перпендикулярны, если прямая, лежащая в одной плоскости, перпендикулярна двум пересекающимся прямым другой плоскости. Построение плоскости перпендикулярной данной плоскости АВС показано на рисунке 30. Через точку М проводится прямая МN, перпендикулярная плоскости АВС. Горизонтальная проекция этой прямой перпендикулярна АС, так как АС является горизонталью, а фронтальная проекция перпендикулярна АВ, так как АВ – фронталь. Затем через точку М проводится произвольная прямая EF. Таким образом, плоскость перпендикулярна АВС и задана двумя пересекающимися прямыми EF и MN.
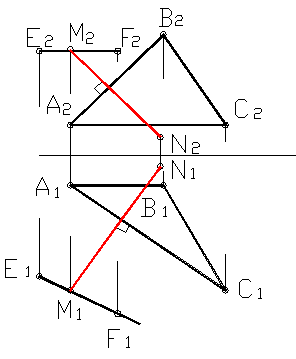
Рисунок 30
Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.
Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.
Проводим перпендикуляр к одному из концов отрезка на горизонтальной плоскости. Откладываем на нем разность высот (ZA-ZB) концов отрезка и достраиваем прямоугольный треугольник. Гипотенуза его является натуральной величиной отрезка, а угол между натуральной величиной и проекцией отрезка – натуральной величиной угла наклона отрезка к плоскости П 1 . Порядок построений на фронтальной плоскости тот же самый. По перпендикуляру откладываем разность глубин концов отрезка (YA-YB). Полученный угол между натуральной величиной отрезка и его фронтальной проекцией – это угол наклона отрезка к плоскости П 2 .
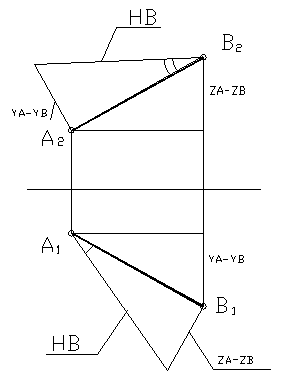
Рисунок 31
1. Сформулируйте теорему о свойстве прямого угла.
2. В каком случае прямая перпендикулярна плоскости?
3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства?
4. Для чего применяется способ прямоугольного треугольника?
5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

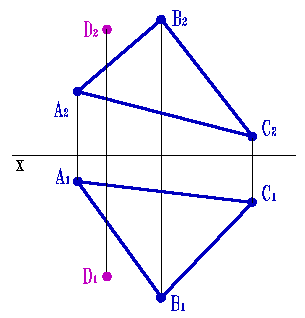
Задача 431 Через точку D провести плоскость.
Условие
Через точку D провести плоскость перпендикулярную плоскости заданной треугольником АВС.
Решение
Через точку D провести плоскость перпендикулярную плоскости заданной треугольником АВС.
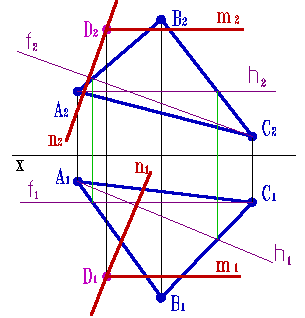
Плоскость (n,m) перпендикулярна плоскость АВС если прямая n перпендикулярна плоскости АВС, а прямая m — произвольная прямая.
Через точку D проведем прямую n перпендикулярную АВС — n1 перпендикулярна h1, а n2 перпендикулярна f2 на основании теоремы о проецировании прямого угла.
Прямая m -произвольная прямая проходящая через точку D.
Плоскость заданная двумя пересекающимися прямыми n и m перпендикулярна АВС.
Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Перпендикулярные плоскости, условие перпендикулярности плоскостей
Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Перпендикулярные плоскости – основные сведения
При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.
При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.
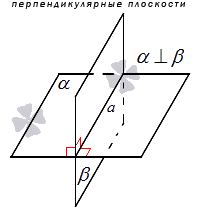
Обозначение перпендикулярности принято писать знаком « ⊥ ». Если в условии дано, что плоскости α и β перпендикулярные, тогда запись принимает вид α ⊥ β . На рисунке ниже показано подробно.
Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.
Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

Перпендикулярность плоскостей – признак и условие перпендикулярности
На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.
Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.
Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.
Доказательство имеется в учебнике по геометрии за 10 — 11 класс, где есть подробное описание. Из признака следует, что, если плоскость перпендикулярна линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.
Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.
Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.
Пусть в трехмерном пространстве задана прямоугольная система координат. Если имеем n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) , являющимися нормальными векторами заданных плоскостей α и β , то необходимым и достаточным условием перпендикулярности векторов n 1 → и n 2 → примет вид
n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0
Отсюда получаем, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) — нормальные векторы заданных плоскостей, а для действительности перпендикулярности α и β необходимо и достаточно, чтобы скалярное произведение векторов n 1 → и n 2 → было равным нулю, а значит, принимало вид n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0 .
Рассмотрим подробнее на примерах.
Определить перпендикулярность плоскостей, заданных в прямоугольной системе координат O x y z трехмерно пространства, заданного уравнениями x — 3 y — 4 = 0 и x 2 3 + y — 2 + z 4 5 = 1 ?
Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.
x — 3 y — 4 = 0 является общим уравнением плоскости, из которого можно сразу преобразовать координаты нормального вектора, равные n 1 → = ( 1 , — 3 , 0 ) .
Для определения координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 перейдем от уравнения плоскости в отрезках к общему.
x 2 3 + y — 2 + z 4 5 ⇔ 3 2 x — 1 2 y + 5 4 z — 1 = 0
Тогда n 2 → = 3 2 , — 1 2 , 5 4 — это координаты нормального вектора плоскости x 2 3 + y — 2 + z 4 5 = 1 .
Перейдем к вычислению скалярного произведения векторов n 1 → = ( 1 , — 3 , 0 ) и n 2 → = 3 2 , — 1 2 , 5 4 .
Получим, что n 1 → , n 2 → = 1 · 3 2 + ( — 3 ) · — 1 2 + 0 · 5 4 = 3 .
Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.
Ответ: плоскости не перпендикулярны.
Прямоугольная система координат O x y z имеет четыре точки с координатами A — 15 4 , — 7 8 , 1 , B 17 8 , 5 16 , 0 , C 0 , 0 , 3 7 , D — 1 , 0 , 0 . Проверить, перпендикулярны ли плоскости А В С и A B D .
Для начала необходимо рассчитать скалярное произведение векторов данных плоскостей. Если оно равно нулю, только в этом случае можно считать, что они перпендикулярны. Находим координаты нормальных векторов n 1 → и n 2 → плоскостей А В С и A B D .
Из заданных координат точек вычислим координаты векторов A B → , A C → , A D → . Получаем, что:
A B → = 47 8 , 19 16 , — 1 , A C → = 15 4 , 7 8 , — 4 7 , A D → = 11 4 , 7 8 , — 1 .
Нормальный вектор плоскости А В С является векторным произведением векторов A B → и A C → , а для A B D векторное произведение A B → и A D → . Отсюда получим, что
n 1 → = A B → × A C → = i → j → k → 47 8 19 16 — 1 15 4 7 8 — 4 7 = 11 56 · i → — 11 28 · j → + 11 16 · k → ⇔ n 1 → = 11 56 , — 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 — 1 11 4 7 8 — 1 = — 5 16 · i → + 25 8 · j → + 15 8 · k → ⇔ n 2 → = — 5 16 , 25 8 , 15 8
Приступим к нахождению скалярного произведения n 1 → = 11 56 , — 11 28 , 11 16 и n 2 → = — 5 16 , 25 8 , 15 8 .
Получим: n 1 → , n 2 → = 11 56 · — 5 16 + — 11 28 · 25 8 + 11 16 · 15 8 = 0 .
Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.
Ответ: плоскости перпендикулярны.
Можно было подойти к решению иначе и задействовать уравнения плоскостей А В С и A B D . После нахождения координат нормальных векторов данных плоскостей можно было бы проверить на выполнимость условие перпендикулярности нормальных векторов плоскостей.
📺 Видео
9. Построение плоскости, перпендикулярной заданнойСкачать

Построение следов плоскостиСкачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

14. Построение следа плоскости, заданной треугольникомСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать
Определить расстояние от точки до плоскости (от точки D до плоскости треугольника ABC)Скачать
Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Перпендикулярные прямые. 6 класс.Скачать

Параллельность прямой к плоскостиСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Линия пересечения плоскостейСкачать

Следы плоскости общего положения заданной фронталью и горизонталью. Начертательная геометрия легкоСкачать