Периметр треугольника блок схема

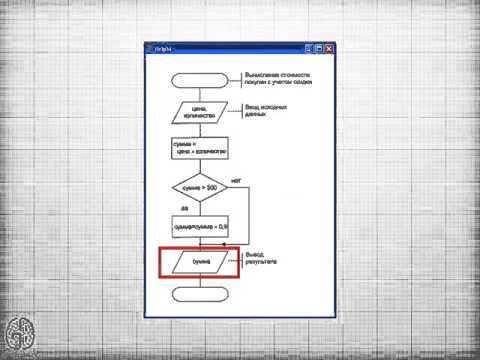
1. Даны длины сторон треугольника A , B , C . Найти площадь треугольника S . Составьте блок-схему алгоритма решения поставленной задачи.

2. Даны координаты вершин треугольника АВС. Найти его периметр. Составьте блок-схему алгоритма решения поставленной задачи.

3. Дана величина A , выражающая объем информации в байтах. Перевести А в более крупные единицы измерения информации. Составьте блок-схему алгоритма решения поставленной задачи

Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Вычисление периметра и площади треугольника

Задание на разработку проекта

Сформулируем содержательную постановку задачи: Создать приложение на VB которое должно вычислять периметр и площадь треугольника по заданным значениям трех его сторон:

Задано: А, В, С – значения сторон треугольника.
Требуется определить: Р – периметр треугольника, S – площадь треугольника.

Ограничения на значения исходных данных и их соотношения: А>0, В>0, C>0, А+В>С, А+C>В, В+C>А одновременно.

Проект должен иметь простой интерфейс пользователя:

• две кнопки управления;
• три поля, отображающие входные данные;
• два поля, отображающие выходные данные.

Формализация и уточнение задания:

Для решения задачи существуют известные формулы:
Р = А + В + С;
S = (формула Герона),

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Учитель информатики

Видео:0.Блок схема. 8 классСкачать

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Видео:Блок-схема циклического алгоритма. Вычисление n!Скачать

Структурное программирование

§ 9. Структурное программирование

Информатика. 11 класса. Босова Л.Л. Оглавление

На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.

Cтруктурное программирование воплощает принципы системного подхода в процессе создания и эксплуатации программного обеспечения ЭВМ. В основу структурного программирования положены следующие достаточно простые положения:

1. алгоритм и программа должны составляться поэтапно (по шагам).
2. сложная задача должна разбиваться на достаточно простые части, каждая из которых имеет один вход и один выход.
3. логика алгоритма и программы должна опираться на минимальное число достаточно простых базовых управляющих структур.

Структурное программирование иногда называют еще «программированием без GO TO». Рекомендуется избегать употребления оператора перехода всюду, где это возможно, но чтобы это не приводило к слишком громоздким структурированным программам.

К полезным случаям использования оператора перехода можно отнести выход из цикла или процедуры по особому условию, «досрочно» прекращающего работу данного цикла или данной процедуры, т.е. завершающего работу некоторой структурной единицы (обобщенного оператора) и тем самым лишь локально нарушающего структурированность программы.

Фундаментом структурного программирования является теорема о структурировании.

Эта теорема устанавливает, что, как бы сложна ни была задача, схема соответствующей программы всегда может быть представлена с использованием ограниченного числа элементарных управляющих структур.

Базовыми элементарными структурами являются структуры: следование, ветвление и повторение (цикл), любой алгоритм может быть реализован в виде композиции этих трех конструкций.

Первая (а) структура — тип последовательность (или просто последовательность), вторая (б) – структура выбора (ветвление), третья (в) – структура цикла с предусловием.

9.1. Общее представление о структурном программировании

Программирование как род занятий и сфера деятельности интенсивно развивается со второй половины прошлого века. За это время сложились определённые технологии, способствующие повышению производительности труда программистов, в том числе сокращению числа ошибок, упрощению отладки, модификации и сопровождения программного обеспечения. Особенно это важно при разработке больших и сложных программных комплексов, осуществляемой усилиями целых коллективов программистов.

Одна из таких технологий — структурное программирование — была разработана ещё в начале 70-х годов прошлого века и связана с именем выдающегося нидерландского ученого Эдсгера Дейкстры (1930-2002).

Структурное программирование — технология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры логически целостных фрагментов (блоков).

Перечислим некоторые принципы структурного программирования.

1. Любая программа строится из трёх базовых управляющих конструкций: последовательность, ветвление, цикл.
2. В программе базовые управляющие конструкции могут быть вложены друг в друга произвольным образом.
3. Повторяющиеся фрагменты программы можно оформить в виде подпрограмм (процедур и функций). В виде подпрограмм можно оформить логически целостные фрагменты программы, даже если они не повторяются.
4. Все перечисленные конструкции должны иметь один вход и один выход.
5. Разработка программы ведётся пошагово, методом «сверху вниз».

О методе разработки алгоритма «сверху вниз» вы получили представление в курсе информатики основной школы. Напомним его ключевые моменты на примере разработки некоторой программы.

Сначала пишется короткий текст основной программы. В ней вместо каждого логически целостного фрагмента вставляется вызов подпрограммы, которая будет выполнять этот фрагмент. Вместо настоящих, работающих, подпрограмм в программу вставляются так называемые заглушки. Как правило, они удовлетворяют требованиям интерфейса заменяемого фрагмента, но не выполняют его функций.

На следующем шаге следует убедиться, что подпрограммы вызываются в правильной последовательности, т. е. верна общая структура программы.

После этого подпрограммы-заглушки последовательно заменяются на полнофункциональные, причём разработка каждой подпрограммы ведётся тем же методом, что и основной программы. На каждом этапе проверяется, что уже созданная программа правильно работает по отношению к подпрограммам более низкого уровня.

Разработка заканчивается тогда, когда ни на одном уровне не останется ни одной заглушки. Полученная программа проверяется и отлаживается.

Такая последовательность гарантирует, что на каждом этапе разработки программист будет иметь дело с обозримым и понятным ему множеством фрагментов, осознавая, что общая структура всех более высоких уровней программы верна.

Действия по вычислению длины отрезка представляют собой логически целостный фрагмент, который целесообразно оформить в виде вспомогательного алгоритма.

9.2. Вспомогательный алгоритм

Пример 1. Применим метод «сверху вниз» для разработки алгоритма нахождения периметра треугольника, заданного координатами своих вершин.

Пусть ХА, ХВ, YA, YB, ХС, YC — координаты вершин треугольника ABC. Его периметр — сумма длин отрезков АВ, ВС и АС.

Из курса геометрии вам известна формула для вычисления длины отрезка АВ по координатам его концов (рис. 2.11):

Действия по вычислению длины отрезка представляют собой логически целостный фрагмент, который целесообразно оформить в виде вспомогательного алгоритма.

Рис. 2.11. Отрезок АВ

Вспомогательный алгоритм — это алгоритм, целиком используемый в составе другого алгоритма.

На рисунке 2.12 представлены:

1) блок-схема алгоритма вычисления периметра треугольника, предполагающая вызов вспомогательного алгоритма Отрезок;
2) блок-схема вспомогательного алгоритма Отрезок.

При вызове вспомогательного алгоритма указываются его параметры (входные данные и результаты). Параметрами вспомогательного алгоритма Отрезок являются величины XI, Y1, Х2, Y2, D. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.

Рис. 2.12. Алгоритм вычисления периметра треугольника и вспомогательный алгоритм Отрезок

Команда вызова вспомогательного алгоритма исполняется следующим образом:

1) формальные входные данные вспомогательного алгоритма заменяются значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма;
2) для заданных входных данных исполняются команды вспомогательного алгоритма;
3) полученные результаты присваиваются переменным с именами фактических результатов;
4) осуществляется переход к следующей команде основного алгоритма.

Каким будет результат работы алгоритма при следующих исходных данных: ХА = 1, ХВ = 2, ХС = 3, YA = 1, YВ = 3, YC = 1.

9.3. Рекурсивные алгоритмы

Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.

Пример 2. Как известно, факториал натурального числа n определяется следующим образом: n! = 1 • 2 • 3 • … • n; 0! считается равным единице (0! = 1).

Иначе это можно записать так:

В определении факториала через рекурсию имеется условие n ? 1, при достижении которого вызов рекурсии прекращается.

В рекурсивном определении должно присутствовать ограничение (граничное условие), при выходе на которое дальнейшая инициация рекурсивных обращений прекращается.

Пример 3. Определим функцию S(n), вычисляющую сумму цифр в заданном натуральном числе n:

Самостоятельно определите функцию К(n), которая возвращает количество цифр заданного натурального числа n.

Пример 4. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

Требуется выяснить, чему равно значение функции F(7). По условию, F(1) = F(2) = 1.

Подобные вычисления можно проводить в уме, а их результаты фиксировать в таблице:

Пример 5. Исполнитель Плюс имеет следующую систему команд:

1) прибавь 1;
2) прибавь 2;
3) прибавь 4.

С помощью первой из них исполнитель увеличивает число на экране на 1, с помощью второй — на 2, с помощью третьей — на 4. Программа для исполнителя Плюс — это последовательность команд. Выясним, сколько разных программ, преобразующих число 20 в число 30, можно составить для этого исполнителя.

Количество программ, с помощью которых можно получить некоторое число n, будем рассматривать как функцию К(n).

Число, меньшее 20, при заданных начальных условиях и системе команд исполнителя Плюс получить невозможно. Следовательно, при n 20 может быть получено из чисел n — 1, n — 2 и n — 4 одной из трёх команд, входящих в систему команд исполнителя — «прибавь 1», «прибавь 2» и «прибавь 4» соответственно. При этом каждая программа получения из исходного числа чисел n-1, n-2 и n-4 удлинится на одну команду и будет приводить к числу n. Следовательно, К(n) = К(n — 1) + + К(n — 2) + К(n — 4).

Запишем все соотношения, определяющие функцию К(n):

Заполним по этой формуле таблицу для всех значений n от 20 до 30:

Итак, существует 169 различных программ, с помощью которых исполнитель Плюс может преобразовать число 20 в 30.

Любой объект, который частично определяется через самого себя, называется рекурсивным. Нас окружает множество рекурсивных объектов. Приведём примеры только некоторых из них.

1. Матрёшка — русская деревянная игрушка в виде расписной куклы, внутри которой находятся подобные ей куклы меньшего размера.

2. Два зеркала, поставленные друг напротив друга, — в них образуются два коридора из затухающих отражений. Это, например, можно наблюдать в спальном железнодорожном вагоне.

3. Примером рекурсивной структуры является замечательное стихотворение Р. Бернса «Дом, который построил Джек» в переводе С. Маршака.

4. Рекурсивную природу имеют геометрические фракталы. На рисунке представлено построение одного из геометрических фракталов — треугольника Серпинского. Чтобы его получить, нужно взять равносторонний треугольник с внутренней областью, провести в нём средние линии и «выкинуть» центральный из четырёх образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трёх треугольников, и т. д.

9.4. Запись вспомогательных алгоритмов на языке Pascal

Запись вспомогательных алгоритмов в языках программирования осуществляется с помощью подпрограмм. В языке Pascal различают два вида подпрограмм: процедуры и функции.

Процедура — подпрограмма, имеющая произвольное количество входных и выходных данных.

Описание процедуры имеет вид:

procedure ( ; var: );

begin

end;

В заголовке процедуры после её имени приводится перечень формальных параметров и их типов. Для вызова процедуры достаточно указать её имя со списком фактических параметров. При этом между фактическими и формальными параметрами должно быть полное соответствие по количеству, порядку следования и типу.

Пример 6. Запишем на языке Pascal программу нахождения периметра треугольника, заданного координатами его вершин. Вспомогательный алгоритм оформим с помощью процедуры.

Выполните программу на компьютере.

Подумайте, каким образом можно модифицировать программу, чтобы вычислять с её помощью периметр n-угольника. Каким образом при решении этой задачи можно использовать массивы?

Функция — подпрограмма, имеющая единственный результат, записываемый в ячейку памяти, имя которой совпадает с именем функции.

Описание функции имеет вид:

В заголовке функции после её имени приводится описание входных данных — указывается перечень формальных параметров и их типов. Там же указывается тип самой функции, т. е. тип результата. В блоке функции обязательно должен присутствовать оператор

Для вызова функции достаточно указать её имя со списком фактических параметров в любом выражении, в условиях (после слов if, while, until) или в операторе write главной программы.

Пример 7. Запишем на языке Pascal программу нахождения периметра треугольника, заданного координатами его вершин. Вспомогательный алгоритм оформим с помощью функции.

Выполните программу на компьютере.

На основе этой программы напишите функцию, вычисляющую площадь треугольника по целочисленным координатам его вершин. Используйте эту функцию для вычисления площади n-угольника.

САМОЕ ГЛАВНОЕ

Структурное программирование — технология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры логически целостных фрагментов (блоков).

Основные принципы структурного программирования заключаются в том, что:

1) любая программа строится из трёх базовых управляющих конструкций: последовательность, ветвление, цикл;
2) в программе базовые управляющие конструкции могут быть вложены друг в друга произвольным образом;
3) повторяющиеся фрагменты программы можно оформить в виде подпрограмм (процедур и функций). В виде подпрограмм можно оформить логически целостные фрагменты программы, даже если они не повторяются;
4) все перечисленные конструкции должны иметь один вход и один выход;
5) разработка программы ведётся пошагово, методом «сверху вниз».

Вспомогательный алгоритм — это алгоритм, целиком используемый в составе другого алгоритма.

Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.

Запись вспомогательных алгоритмов в языках программирования осуществляется с помощью подпрограмм. В языке Pascal различают два вида подпрограмм: процедуры и функции.

Вопросы и задания

1. В чём заключается сущность структурного программирования? Какие преимущества обеспечивает эта технология?

2. Какой алгоритм называется вспомогательным?

3. Вспомните, в чём состоит суть метода последовательного построения (уточнения) алгоритма. Как он называется иначе?

4. Опишите основные шаги разработки программы методом «сверху вниз».

5. Дан прямоугольный параллелепипед, длины рёбер которого равны а, b и с.

Требуется определить периметр треугольника, образованного диагоналями его граней. Какой алгоритм целесообразно использовать при решении этой задачи в качестве вспомогательного?

6. Какой вспомогательный алгоритм называется рекурсивным? Что такое граничное условие и каково его назначение в рекурсивном алгоритме?

7. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

Требуется выяснить, чему равно значение функции F(10).

8. Исполнитель Калькулятор имеет следующую систему команд:

1) прибавь 1;
2) умножь на 2.

С помощью первой из них исполнитель увеличивает число на экране на 2, с помощью второй — в 2 раза.

1) Выясните, сколько разных программ, преобразующих число 1 в число 20, можно составить для этого исполнителя.
2) Сколько среди них таких программ, у которых в качестве промежуточного результата обязательно получается число 15?
3) Сколько среди них таких программ, у которых в качестве промежуточного результата никогда не получается число 12?

9. Попробуйте найти рекурсивные синтаксические структуры:

1) в поэме А. Блока «Двенадцать»;
2) в стихотворении М. Лермонтова «Сон»;
3) в романе М. Булгакова «Мастер и Маргарита»;
4) в фольклоре.

10. Найдите информацию о таких геометрических фракталах, как Снежинка Коха, Т-квадрат, Н-фрактал, кривая Леви, Драконова ломаная.

11. Напишите программу вычисления значения функции F(n), рассмотренной в примере 4 этого параграфа. Вычислите с её помощью значение функции F(7).

12. Напишите программу вычисления

13. Дана программа:

Не выполняя программу на компьютере, выясните, что получится в результате работы этой программы.

Проверьте свой результат, выполнив программу на компьютере.

Дополнительные материалы к главе смотрите в авторской мастерской.

💥 Видео

Решаем задачи в виде блок-схемы (7 класс)Скачать

Найдите периметр треугольникаСкачать

Самый подробный урок про Блок-схемы, Понимание, Чтение и Создание блок-схемСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Периметр прямоугольника. Как найти периметр прямоугольника?Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Блок схема алгоритма (часть 1)Скачать

№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Решение простых задач на python | Площадь и периметр прямоугольного треугольникаСкачать

Решение задачи на компьютере. Последовательное конструирование алгоритмаСкачать

№156. Периметр треугольника ABC равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона ABСкачать

Вычисление площади и периметра прямоугольника в ПаскальСкачать

Блок схема.Работа в ворде. WordСкачать

Python для чайников! Блок схема: линейная, развлетленная, циклическая.Скачать

Нахождение площади треугольника в С++Скачать

основы программирования 6 алгоритмы и блок схемыСкачать