Методы, которое мы сейчас рассмотрим, также можно использовать для нахождения пересечения прямой и плоскости. Пересечения с более сложными многоугольниками можно найти путем их триангуляции.
Исходник, помещенный внизу, скорее иллюстрирует путь решения, нежели действительно эффективен.
Модель и соглашения о наименованиях обозначены на данном рисунке
Процедура, которую мы сейчас рассмотрим, будет получать на входе отрезок, заданный двумя точками, и треугольник, заданный тремя вершинами.
Решение будет состоять из следующих шагов
- Проверка: параллельна ли прямая плоскости
- Нахождение пересечения плоскости треугольника с отрезком
- Проверка: лежит ли точка пересечения на отрезке
- Проверка: лежит ли точка пересечения внутри треугольника
Точка пересечения P находится подстановкой в уравнение плоскости Ax + By + Cz + D = 0 уравнения прямой P = P1 + мю (P2 — P1).
Заметим, что значения A,B,C являются компонентами вектора нормали к плоскости, который можно найти взятием векторного произведения любых двух нормализованных векторов, например
D можно затем получить, подставлив одну из вершин в уравнение плоскости, например
Это дает нам выражение для мю, из которого точка пересечения P может быть найдена через уравнение прямой.
Если знаменатель выше равен нулю, то прямая параллельна плоскости и пересечения нет. Для того, чтобы точка пересечения лежала на отрезке, мю должно принимать значения от 0 до 1.
Ну и в последнюю очередь необходимо установить, лежит ли точка пересечения внутри треугольника, ограниченного Pa, Pb, Pc.
Способ, которым мы воспользуемся, опирается на то, что сумма внутренних углов вида вершина-точка-вершина равна 2pi, если точка внутри треугольника. Для точки вне треугольника эта сумма будет меньше. Очевидно, сумма берется для одной точки — точки пересечения линии и плоскости и по всем сочетаниям вершин, как проиллюстрировано на рисунке
Если мы вычислим единичные векторы Pa1, Pa2, Pa3 как (мы проверяем точку P на принадлежность треугольнику)
Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Пересечение линии и треугольника в 3D
У меня есть линия и треугольник где-то в трехмерном пространстве. Другими словами, у меня есть 3 точки ([x, y, z] каждая) для треугольника и две точки (также [x, y, z]) для линии.
Мне нужно найти способ, надеюсь, с помощью C ++, чтобы выяснить, пересекает ли когда-либо линия треугольник. Линия, параллельная треугольнику и имеющая более одной общей точки, должна рассматриваться как «не пересекающаяся».
Я уже сделал некоторый код, но он не работает, и я всегда получаю ложь, даже когда визуальное представление ясно показывает пересечение.
А вот и определение inside ()
Видео:Нахождение точки пересечения прямой и треугольникаСкачать

Решение
1) Если вы просто хотите знать будь то линия пересекает треугольник (без пересечения):
Пусть p1, p2, p3 обозначают ваш треугольник
Выберите две точки q1, q2 на линии очень далеко в обоих направлениях.
Пусть SignedVolume (a, b, c, d) обозначает подписанный объем тетраэдра a, b, c, d.
Если SignedVolume (q1, p1, p2, p3) и SignedVolume (q2, p1, p2, p3) имеют разные знаки AND
SignedVolume (q1, q2, p1, p2), SignedVolume (q1, q2, p2, p3) и SignedVolume (q1, q2, p3, p1) имеют один и тот же знак, тогда существует пересечение.
SignedVolume (a, b, c, d) = (1/6) * точка (крест (b-a, c-a), d-a)
2) Теперь, если вы хотите пересечение, когда тест в 1) проходит
запишите уравнение прямой в параметрической форме: p (t) = q1 + t * (q2-q1)
Запишите уравнение плоскости: точка (p, N) — точка (p, p1) = 0, где N = крест (p2-p1, p3-p1)
Введите p (t) в уравнение плоскости: точка (q1 + t * (q2-q1), N-p1) = 0
Выведите t = -dot (q1, N-p1) / dot (q1, q2-q1)
Точка пересечения q1 + t * (q2-q1)
Видео:Пересечение прямой и плоскостиСкачать

Другие решения
Чтобы найти пересечение между линией и треугольником в 3D, используйте следующий подход:
- Вычислить плоскость, поддерживающую треугольник,
Пересечь линию с плоскостью, поддерживающей треугольник:
- Если пересечения нет, то пересечения с треугольником нет.
Если есть пересечение, убедитесь, что точка пересечения действительно лежит в треугольнике:
- Каждое ребро треугольника вместе с нормалью плоскости, поддерживающей треугольник, определяет полупространство, ограничивающее внутреннюю часть треугольника (соответствующая ограничивающая плоскость может быть получена из вершин нормали и ребер),
- Убедитесь, что точка пересечения лежит внутри всех краевых полупространств.
Вот пример кода с подробными вычислениями, которые должны работать:
Некоторые комментарии к коду размещены с вопросом:
- Предопределенные операции ofVec3f ( .dot() а также .cross() для геометрических продуктов и т. д.) следует отдавать предпочтение при их наличии (более читабельно, избегать ошибок при реализации и т. д.
- Код вначале следует описанному выше подходу, но затем проверяет только то, что точка пересечения находится в трехмерной ограничивающей рамке отрезка отрезка [P1, P2]. Это в сочетании с возможными другими ошибками может объяснить, почему результаты неверны.
- Можно убедиться, что точка пересечения находится в трехмерном ограничивающем прямоугольнике (целого) треугольника. Хотя этого недостаточно, чтобы гарантировать пересечение, его можно использовать для того, чтобы отбирать точки, которые явно не пересекаются, и избегать дальнейших сложных вычислений.
Видео:Пересечение прямой линии с плоскостью Определение видимости прямойСкачать

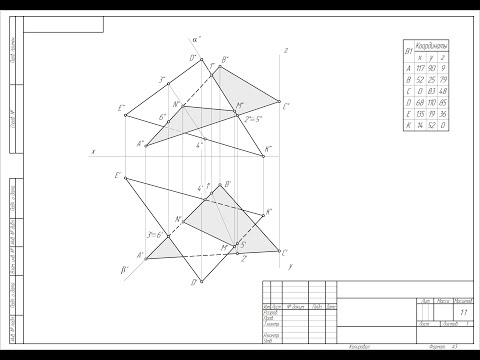
Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.
1. Строим проекции треугольника АВС.
2. Строим проекции треугольника EDK.
3. Находим точку пересечения стороны АС с треугольником EDK
4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN
5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.
6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.
7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.
Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.
8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.
💥 Видео
Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать
Линия пересечения плоскостейСкачать

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать

Точка встречи прямой с плоскостьюСкачать

Пересечение прямой и плоскости Определение видимости прямойСкачать

Точка пересечения прямой с плоскостью заданную треугольником #задачипоначертательнойгеометрииСкачать

15. Определение точки пересечения прямой с плоскостью, заданной треугольникомСкачать

Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

Нахождение пересечения двух треугольниковСкачать
Построение точки пересечения прямой с плоскостью, заданной следамиСкачать
Пересечение прямой и плоскостиСкачать

Пересечение прямой и отрезкаСкачать

9. Пересечение прямой с плоскостьюСкачать

Определение видимости.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Построение линии пересечения двух треугольников.Скачать