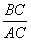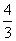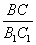- Корзина
- Параллельный перенос
- Поворот плоскости вокруг точки на угол
- Подобные треугольники
- Параллельный перенос и поворот
- Параллельный перенос
- Поворот
- Готовые работы на аналогичную тему
- Примеры задач на параллельный перенос и поворот
- Метод плоскопараллельного перемещения
- Определение натуральной величины треугольника
- Определение расстояния между параллельными прямыми
- 📽️ Видео
Корзина

Теоретический урок по предмету математики для решения задач по теме «Параллельный перенос, поворот плоскости и подобные треугольники».
Содержание данной онлайн страницы электронного справочника для школьников:
- – тема «Параллельный перенос» представлена на примере решения задач 145 — 148;
- – в контрольных работах с номерами 149 — 154 данной рабочей тетради по математике рассматривается поворот плоскости вокруг точки на угол;
- – повторение курса геометрии 9 класса в решениях приведено на примере заданий 155 — 173: углы треугольника, площадь треугольника через катеты и гипотенузу, вычисление радиуса описанной окружности, стороны ромба, подобные треугольники.
Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Параллельный перенос


Параллельным переносом на вектор 


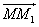

Задача 145.



A → A1 : 


B → B1 : 


Теорема:
При параллельном переносе на вектор 

f – параллельный перенос на вектор 
M 

N 



Точка M переводится движением в точку M1 с условием, что два вектора равны: M 



Точка N переводится движением в точку N1 с условием, что два вектора равны: N 



Следовательно, полученные отрезки параллельны MM1 || NN1 и построенные отрезки равны MM1 = NN1
Значит, четырехугольник MM1N1N – параллелограмм.
Поэтому MN = M1N1, значит f – движение.

Задача 146.
A 




B 




C 


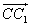


A 




B 




C 


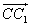



Задача 147.
точка D лежит на AC: D 
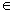
точка C лежит на AD: C 
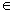
BC 
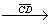
б) Доказать: ABB1D – равнобедренная трапеция
1) От точки B проведем прямую a, параллельную вектору 

2) Точка B переводится движением в точку B1



3) Проведем прямую B1D, параллельную отрезку BC:
Рассмотрим четырехугольник BB1DC.
Т.к. основания BB1 || CD и боковые стороны BC || BD параллельны, то BB1DC – параллелограмм (по определению)
По свойству параллелограмма:
основания BB1 = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B1D
Т.к. BB1 || AD параллельны и AB 
Т.к. AB = B1D, то ABB1D – равнобедренная трапеция.
Задача 148.
Дано: 
вектор 
окр (O;R) 

ΔABC 

EFPQ 

как показано на рисунке.
Видео:Параллельный перенос точки, отрезка, треугольника, четырехугольника. Геометрия 8 классСкачать

Поворот плоскости вокруг точки на угол
Определение:




O – центр поворота
α – угол поворота
Задача 149.


α = 75° (против часовой стрелки)
O – центр поворота
1) A 
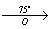


2) B 
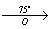


Теорема:
Поворот является движением.


α – угол поворота (против часовой стрелки)
точка O – центр поворота
Тогда треугольники равны ΔOMN = ΔOM1N1 по двум сторонам и углу между ними:




Тогда MN = M1N1, значит, f – движение.
Задача 150.
точка O – центр поворота


1) A 
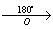


2) B 
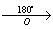


Задача 151.
точка A – центр поворота
α = 160° (против часовой стрелки)
1) B 
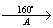


2) C 
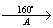


Задача 152.
точка O – центр поворота


1) A 
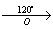


2) B 
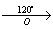


Задача 153.
точка C – центр окружности (C; R)
точка O – центр поворота
угол поворота α = 60° (против часовой стрелки)
а) точка C и точка O не совпадают
б) точка C и точка O совпадают


1) проведем луч CO
2) C 
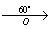



Т.к. точка О – центр поворота и точка С – центр окружности совпадают, то окружности (C;R) и (C1;R) будут тоже совпадать.

Задача 154.
Δ ABC – равнобедренный, равносторонний
D – точка пересечения биссектрис
D – центр поворота
угол поворота α = 120°
ΔABC 

Т.к. Δ ABC – правильный, то все углы в нем равны 60°.
Т.к. точка D – центр описанной и вписанной окружности, то
Δ ABD = Δ BDC = Δ DAC (по трем сторонам).
Следовательно, что 





A 

B 

C 

Таким образом, Δ ABC отображается на себя.
Повторение.
Задача 155.






Найти: наибольший угол треугольника
Пусть x – коэффициент пропорциональности. Зная, что сумма углов в треугольнике равна 180°, составим и решим уравнение:
3x + 7x + 8x = 180
Наибольший угол 

Задача 156.
треугольник ΔABC – равнобедренный,
один угол больше другого:






Найти: угол при основании треугольника
Пусть x° – угол при основании треугольника. Зная, что сумма углов в треугольнике составляет 180°, составим и решим уравнение:
(x + 60°) + x + x = 180°
Значит, 

Задача 157.
треугольник ΔABC – прямоугольный
c = 26 см – гипотенуза
Найти: больший катет b
Пусть x – коэффициент пропорциональности. По теореме Пифагора составим и решим уравнение:
(5x) 2 + (12x) 2 = 26 2
25x 2 + 144x 2 = 676
b = 12 • 2 = 24 (см)
Задача 158.


c = 13 – гипотенуза
По теореме Пифагора получаем:
a = 
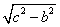

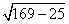

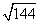
Тогда площадь треугольника
SΔABC = 


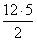
= 30 (квадратных единиц)
Задача 159.
треугольник ΔABC – равнобедренный,


c = 4 
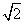
Найти: площадь треугольника SΔABC = ?
SΔABC = 

Т.к. Δ ABC – равнобедренный, то углы при основании по 45° и катеты равны a = b.
По теореме Пифагора получаем:
Тогда (4 
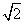
Тогда площадь треугольника
SΔABC = 


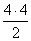
= 8 (квадратных единиц)
Задача 160.




Найти: радиус описанной окружности R = ?
Т.к. AH – медиана, то CH = 

По теореме Пифагора получаем:
Тогда CH = 


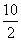
Точка H – центр описанной окружности
Т.к. R = AH, то R = AH = CH = 5 ед.
Задача 161.


соотношение острых углов




AC = 4 
Найти: радиус описанной окружности R = ?


Тогда 



Следовательно, BC = 

По теореме Пифагора получаем:
AC 2 + 
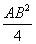
AC 2 = 

AB 2 = 
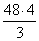
R = AD = BD = 8 : 2 = 4 (ед)
Задача 162.




радиус описанной окружности
Тогда AB = 2,5 • 2 = 5
По теореме Пифагора получаем:
AC = 
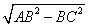

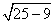

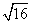




tg 


0,6 = 
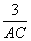

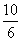
Задача 164.


Найти: 



Т.к. AH = AC, то Δ AHC – равнобедренный.
Точка H – радиус вписанной окружности, поэтому AH = CH, но AH = AC, следовательно, AH = CH = AC.
Тогда Δ AHC – равносторонний.
Значит, 





Задача 165.
треугольник Δ ABC – правильный, равносторонний,
SΔABC = 
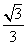
Найти: длину биссектрисы BH = ?


Рассмотрим Δ ABC – равнобедренный, где




Тогда BH – медиана, высота.
Значит, перпендикулярны отрезки BH 
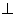
Рассмотрим треугольники Δ ABH и Δ BHC.
AB = BC, по условию.
AH = CH, BH – медиана.
Значит, треугольники равны Δ ABH = Δ BHC.
Т.е. SΔABH = 




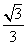

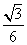
SΔABH = 

Рассмотрим треугольник Δ ABH.
Т.к. BH – биссектриса, то угол 

AH = 

SΔABH = 


AB • BH = 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
AB 2 = 

BH 2 = 

BH = 
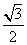
Используя результат (**) в уравнении (*), получаем
AB • 
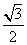

AB 2 = 
AB = 
Тогда AB • BH = 






Задача 166.
треугольник Δ ABC – правильный, равносторонний,


R = 
Найти: площадь треугольника
Рассмотрим Δ ABO (AO = BO = R) 

Проведем из вершины O к AB высоту OH.
Рассмотрим Δ AOH, где 

Т.к. 







OH = 


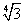

По теореме Пифагора получаем:
OH 2 + AH 2 = OA 2

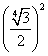

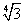



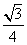
= 
AH 2 = 
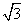

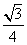

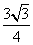



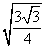

Тогда площадь треугольника
SΔAOH = 




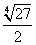

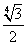

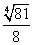

Следовательно, SΔABO = 2 • SΔAOH = 2 • 
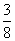


Тогда площадь треугольника
SΔABC = 3 • SΔABO = 3 • 


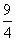




Площадь ромба SABCD = 384
Соотношение диагоналей ромба:
Найти: сторону ромба AB = ?
SABCD = 

Пусть x – коэффициент пропорциональности. Тогда
SABCD = 

Следовательно, диагональ BD = 4x = 4 • 8 = 32
AC = 3x = 3 • 8 = 24
Поэтому половина диагонали AO = 



BO = 



По теореме Пифагора получаем:
AO 2 + BO 2 = AB 2
Сторона ромба AB = 
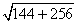

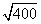
Задача 168.
треугольник Δ ABD – равнобедренный,


Найти: площадь треугольника
SΔABD = 

Проведем высоту BH к основанию AD.
По свойству равнобедренного треугольника:
BH – медиана, биссектриса, высота.
Т.к. BH – медиана, то AH = DH = 16 : 2 = 8 (ед.)
Рассмотрим треугольник Δ ABH, где угол 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
BH = 
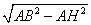

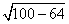

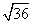
Тогда площадь треугольника
SΔABD = 



Ответ: площадь треугольника SΔABD = 48 кв.ед.

Задача 169.
треугольник Δ ABC –равнобедренный,
основание AC больше высоты BH на 15: AC > BH на 15
Найти: основание AC = ?
Т.к. треугольник Δ ABC –равнобедренный, то BH – высота, медиана, биссектриса.
Тогда AC = AH + CH = AH + AH = 2 AH
Рассмотрим Δ ABH – прямоугольный.
Пусть AC = (x) ед. 


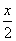
Тогда AB = (x – 15) ед. (по условию).
По теореме Пифагора решим уравнение:
(x – 15) 2 = ( 
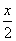



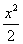
4 (x 2 – 30x) = x 2
4x 2 – 120x = x 2
3x 2 – 120x = 0 | : x
Таким образом, 40 ед. – длина основания.
Ответ: AC = 40 ед.
Видео:Перенос треугольника по векторуСкачать
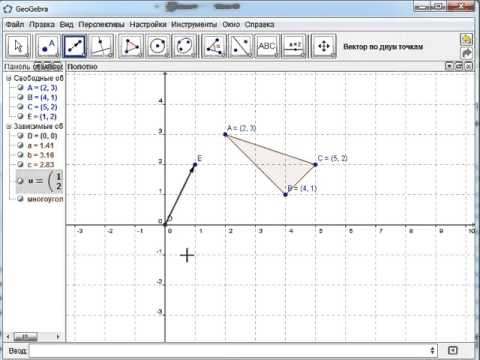
Подобные треугольники
Задача 170.






CH – биссектриса угла 

Доказать: подобие треугольников
Δ BHC 









Т.к. CH – биссектриса угла 





Рассмотрим Δ BHC








Тогда 



Поэтому треугольники подобны Δ BHC 



верхнее основание BC = 4 см
нижнее основание AD = 10 см
диагональ BD = 8 см
часть диагонали BO = ?
соотношение периметров треугольников


Углы равны 



Углы равны 



Тогда треугольники подобны Δ BCO 




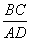

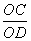







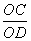













Пусть BO = x, AO = 8 – x. Тогда 10x = 4 • (8 – x)
x = 2 

Следовательно, BO = 2 



Ответ: BO = 2 



Задача 172.
ΔABC 



P (ΔABC) = 12 +16 + 20 = 48 (дм)
Т.к. треугольники подобны, то

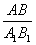

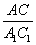




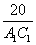


Тогда соотношение периметров треугольников

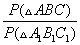
Из равенств (*) и (**) следует



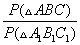




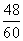

B1C1 = 
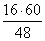
Тогда 





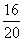



A1B1 = 
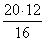
Задача 173.


стороны трапеции пересекаются в точке M:
Рассмотрим треугольники ΔAMD и ΔBMC:








Тогда, по первому признаку подобия треугольников:
треугольники подобны Δ AMD 


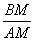

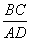

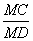


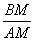

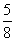
но AM = AB + BM = 3,9 + BM
8 • BM = 5 (3,9 + BM)

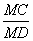

Видео:9 класс, 32 урок, Параллельный переносСкачать

Параллельный перенос и поворот
Вы будете перенаправлены на Автор24
Видео:#192 ПОВОРОТ И ПЕРЕНОС // ТРЕУГОЛЬНИКСкачать

Параллельный перенос
Введем определение параллельного переноса на вектор. Пусть нам дан вектор $overrightarrow$.
Рисунок 1. Параллельный перенос
Введем следующую теорему.
Параллельный перенос является движением.
Доказательство.
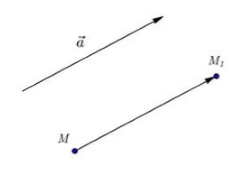
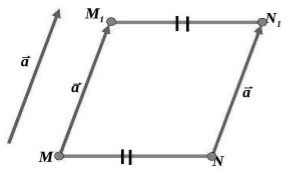
Пусть нам даны точки $M и N$. Пусть при их параллельном переносе на вектор $overrightarrow$ эти точки отображаются в точки $M_1$ и $N_1$, соответственно (рис. 2).
Рисунок 2. Иллюстрация теоремы 1
Значит четырехугольник $_1N_1N$ — параллелограмм и, следовательно, $MN=M_1N_1$. То есть параллельный перенос сохраняет расстояние между точками. Следовательно, параллельный перенос является движением.
Теорема доказана.
Видео:ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать

Поворот
Введем определение поворота вокруг точки $O$ на угол $alpha $.
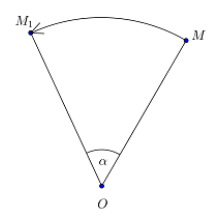
Поворот вокруг точки $O$ на угол $alpha $ — отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $_1=OM, angle M_1=angle alpha $ (Рис. 3).
Рисунок 3. Поворот
Готовые работы на аналогичную тему
Введем следующую теорему.
Поворот является движением.
Доказательство.
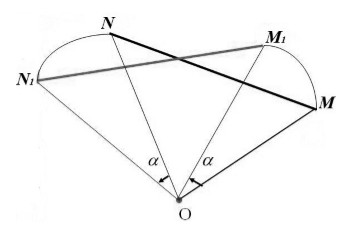
Пусть нам даны точки $M и N$. Пусть при их повороте вокруг точки $O$ на угол $alpha $ они отображаются в точки $M_1$ и $N_1$, соответственно (рис. 4).
Рисунок 4. Иллюстрация теоремы 2
Так как, по определению 2, $_1=OM, _1=ON$ и $overrightarrow<_1>=overrightarrow$, а ,$angle MON=angle M_1ON_1$, то
Следовательно, $MN=M_1N_1$. То есть поворот сохраняет расстояние между точками. Следовательно, поворот является движением.
Теорема доказана.
Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Примеры задач на параллельный перенос и поворот
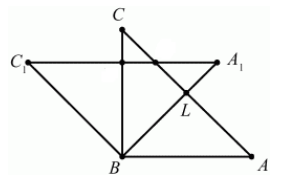
Построить треугольник $A_1B_1C_1$,образованный поворотом вокруг точки $B$ на угол $^0$ равнобедренного прямоугольного (с прямым углом $B)$ треугольника $ABC$.
Решение.
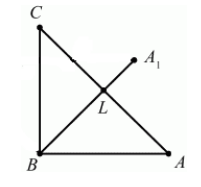
Очевидно, что точка $B$ перейдет сама в себя, то есть $B_1=B$. Так как поворот производится на угол, равный $^0$, а треугольник $ABC$ равнобедренный, то прямая $BA_1$ проходит через точку $L$ — середины стороны $AC$. По определению, отрезок $BA_1=BA$. Построим его (Рис. 5).
Построим теперь вершину $C_1$ по определению 2:
[angle CBC_1=^0, BC=BC_1]
Соединим все вершины треугольника $A_1B_1C_1$ (Рис. 6).
Решение закончено.
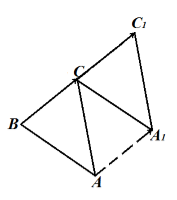
Построить параллельный перенос треугольника $ABC$ на вектор $overrightarrow$.
Решение.
Перенесем каждую вершину треугольника на вектор $overrightarrow$. Получаем треугольник $CA_1C_1$ (рис. 7).
Решение закончено.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 15 04 2021
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Метод плоскопараллельного перемещения
В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.
Свойства плоскопараллельного перемещения:
- При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
- При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»1 и D»1.
- При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.
Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П2.
- Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’1D’1 = C’D’.
- По линиям связи определяем недостающие проекции C»1 и D»1. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.
Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П2. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.
- После первого преобразования отрезок MN займет положение параллельно плоскости П1. Сначала строится M»1N»1 = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’1 и N’1.
- Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’1N’1 в положение M’2N’2, перпендикулярное оси X. После этого точки M»2 = N»2 определяются по линиям связи.
Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Определение натуральной величины треугольника
Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.
- Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
- Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’1D’1 = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’1B’1C’1 = A’B’C’. По линиям связи определяем точки A»1, B»1, C»1.
- Перемещаем проекцию A»1B»1C»1 треугольника ABC в положение A»2B»2C»2, параллельное оси X, соблюдая равенство A»2B»2C»2 = A»1B»1C»1. По линиям связи определяем точки A’2, B’2, C’2. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’2B’2C’2.
Видео:Параллельный переносСкачать

Определение расстояния между параллельными прямыми
Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.
Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’2 и B’2, расстояние между которыми является искомым. Показанные на рисунке величины d1 и d2 являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.
📽️ Видео
11 класс, 12 урок, Параллельный переносСкачать

2 3 проекция точки на конусеСкачать

Определение преобразований | Геометрические преобразования и Конгруэнтность | ГеометрияСкачать

Геометрия 9 класс : Параллельный перенос и поворотСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Параллельный перенос. Координаты точек при параллельном переносе. Геометрия 8 классСкачать

Урок 8. Параллельный перенос. Декартовы координаты на плоскости.Скачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать