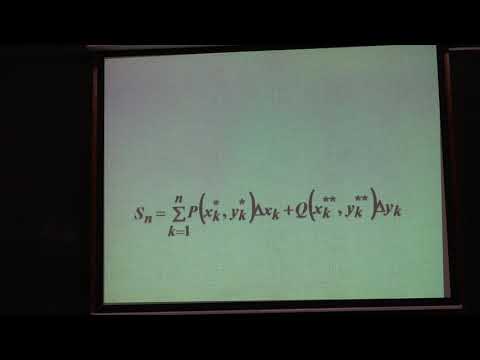Параметризация окружности на комплексной плоскости

Областью в комплексной плоскости называется множество D точек этой плоскости, обладающее свойствами:

1) открытости – вместе с точкой из D этому множеству принадлежит и достаточно малая окрестность с центром в этой точке;

2) связности – любые две точки D можно соединить ломаной, целиком состоящей из точек D.

Примером области могут служить окрестности точек на комплексной плоскости. Под e-окрестностью точки z₀ понимают открытый круг радиуса e с центром в этой точке: |z – z₀| 2 + (y – 1) 2 = e 2 – окружность радиуса e с центром в точке х = 0, у = 1 комплексной плоскости.

Область с присоединенной к ней границей называют замкнутой и обозначают D. Будем в дальнейшем предполагать, что граница области состоит из конечного числа замкнутых линий, разрезов (дуг) и точек. Линии и разрезы, входящие в состав границы будем предполагать всегда кусочно-гладкими.

Область называется односвязной, если граница состоит из одной связной линии. Область называется многосвязной, если граница области состоит из нескольких связных частей, например: двухсвязной, трехсвязной и т.д. – по числу не связных между собой частей границы. На рис. 2.2,б – пример двухсвязной области.

Обход односвязной области считается положительным, если она остается по левую руку (контур обходится против хода часовой стрелки). На рис. 2.2,б сделан разрез l, а обход области изображен положительным (область в результате разреза стала односвязной).

Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или неограниченной, односвязной или многосвязной.

а) поэтому получим: . Область (рис. 2.3) – замкнутая, ограниченная, односвязная.

б) и – лучи, выходящие из начала координат (рис. 2.4). Все точки, удовлетворяющие неравенству б) лежат внутри угла, образованного этими лучами, и на сторонах этого угла. Следовательно, область замкнутая, неограниченная, односвязная.

Неравенство означает, что расстояние каждой точки z от точки больше 1, но меньше 2. Поэтому областью есть кольцо (его внутренность), ограниченное концентрическими окружностями с центром в точке . Область – открытая, ограниченная, двухсвязная (рис. 2.5).

г) Неравенство равносильно или

или, возведя в квадрат обе части, получим:

х 2 + у 2 – 2у + 1 2 + у 2 + 2у + 1.

Отсюда: – верхняя полуплоскость (рис.

Вывод: область у>0 – открытая, неограниченная, односвязная (рис. 2.4).

Определение. Кривая называется непрерывной, если она может быть задана параметрическими уравнениями:

в которых – непрерывные функции на отрезке .

Например, окружность ; дуга окружности

; дуга параболы – непрерывные кривые; гипербола не является непрерывной, так как функции эти при и имеют точки разрыва.

С помощью комплексного переменного параметрические уравнения кривой (2.18) можно записать в виде одного уравнения:

Например, уравнение эллипса с полуосями a и b можно записать:

уравнение окружности радиуса R

уравнение окружности с центром в точке запишется так:

Задачи для упражнений

1) Построить в комплексной плоскости линии, точки которых удовлетворяют уравнениям:

а) б) в) г) д) е) ж) ; з)

2) Построить на комплексной плоскости z области, заданные условиями:

Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или нет, односвязной или многосвязной.

3) Какие кривые определяются следующими уравнениями:

Ответы: а) б) в) г) д)

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Видео:Линии и области на комплексной плоскостиСкачать

Прямая и окружность на плоскости комплексных чисел

Пусть произвольной точке М плоскости комплексных чисел соответствует комплексное число. Из равенств и однозначно выражаются декартовы координаты х и у точки М через комплексные числа и :

Поэтому комплексные числа z и называются сопряженными комплексными координатами этой точки.

Формулы (1) позволяют осуществить переход от уравнения геометрической фигуры в декартовых координатах к ее уравнению в сопряженных комплексных координатах. Однако сейчас мы предпочли непосредственное рассмотрение уравнений в сопряженных комплексных координатах.

Геометрический смысл уравнения: .

Найдем множество точек плоскости, сопряженные комплексные координаты которых удовлетворяют уравнению:

Сначала выделим особый случай, когда с=0. Тогда имеем систему относительно и :

второе уравнение которой получается из первого переходом к сопряженным числам. Уравнивая коэффициенты при , путем вычитания второго уравнения из первого получаем:

Если , т.е. , то решением полученного уравнения, а значит, и решением исходного уравнения будет единственное число z=0. При уравнение напишем в виде . Модули левой и правой частей равны. Необходимо, чтобы , откуда . Этому условию удовлетворяет каждая точка прямей m, проходящей через начало под углом к действительной оси (рис.1).

задается прямая при и точка при .

Пусть теперь . Свободный член уравнения (2) можно всегда сделать действительным числом путем умножения обеих частей уравнения на с. Поэтому сразу будем полагать Тогда имеем систему:

из которой получаем: . Рассмотрим возможные случаи.

Если , то и подстановкой в исходное уравнение получаем: или .

При его решение единственно:

При решений нет.

Если , то и , т. е. . В этом случае уравнением (2) при прямая. В самом деле, возьмем точку и вектор точки В(b) и рассмотрим множество точек М(z), для каждой из которых (MQ)(OB):

Очевидно, это множество есть прямая. При и уравнение (4) эквивалентно уравнению (2).

Таким образом, при и уравнение (2) есть уравнение прямой, которая проходит через точку перпендикулярно вектору .

Наконец, отметим случай, когда , но . Тогда система:

приводит к противоречию: , т.е. .

Подведем итоги. Уравнением , в котором хотя бы один из коэффициентов a и b отличен от нуля, задается:

• 1) прямая при |а|=|b|, с=0, а также при ;
• 2) единственная точка при ;
• 3) пустое множество в иных случаях, т. е. при |a| = |b|, , а также при , .

Достигнув поставленной цели, возвратимся снова к системе:

не налагая ограничений на коэффициенты а, b, с, кроме того, что a и b не равны нулю одновременно. Уравнивая коэффициенты при , приходим к уравнению , которое:

• а) имеет единственное решение при ;
• б) имеет бесконечное множество решений при и ;
• в) не имеет решений при и .

Отсюда и на основании результата предыдущих исследований получаем, что уравнение определяет:

• а) единственную точку при
• б) прямую при и ;
• в) пустое множество при и .

прямой в сопряженных комплексных координатах будем называть приведенным уравнением прямой.

6. Две прямые. Расстояние от точки до прямой

Пусть прямая т задана приведенным уравнением . Так как она перпендикулярна вектору , то вектор будет ей параллелен (рис.2).

Следовательно, ориентированный угол от оси х до прямой т равен аргументу числа ai:

Положительно ориентированный угол от прямой до прямой равен углу между их направляющими векторами и :

Формулы (6) и (7) позволяют находить соответствующие углы с точностью до слагаемого .

Из формулы (7) вытекает критерий перпендикулярности и критерий параллельности прямых и . В самом деле, чисто мнимое число. Это значит, что , или:

При или получаем:

Если прямая проходит через точку , то и ее уравнение можно написать в виде:

В силу условия (8) перпендикулярности для прямой, перпендикулярной данной, коэффициентами при, z и будут соответственно числа а и . Поэтому на основании уравнения (10) получаем уравнение:

прямой, проходящей через точку перпендикулярно прямой . Решение системы:

основания M₁ перпендикуляра, опущенного из точки на прямую .

Так как расстояние d от точки M₀ этой прямой равно, то:

Геометрический смысл, уравнения .

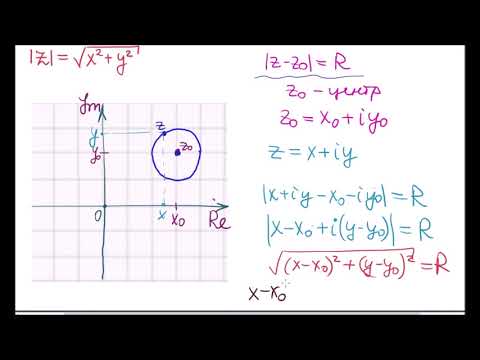
Из формулы расстояния между двумя точками получается уравнение окружности по ее центру S (s) и радиусу R :

Пусть дано уравнение:

в котором на комплексные коэффициенты а, b, с не накладывается заранее никаких условий. Требуется найти множество точек, координаты которых ему удовлетворяют. С этой целью удобно представить его в эквивалентном виде:

Рассмотрим все возможные случаи для коэффициентов а, b, с.

1. Сравнивая уравнение (16) с уравнением (14) окружности, приходим к выводу, что уравнение (16), а значит, и уравнение (15) задают окружность тогда и только тогда, когда и ab- с — действительное число. Так как в этом случае , то с должно быть действительным числом.

есть уравнение окружности с центром s=-b и радиусом .

• 2. При и с=ab уравнению (16) удовлетворяет единственная точка s=-b. В частности, этот случай имеет место при а=b=с=0. Соблюдая аналогию, говорят, что уравнением задается окружность с центром s=-b нулевого радиуса.
• 3. Если , , но , то — чисто мнимое число. Полагаем , тогда (16) можно записать так:

Уравнению (18) не удовлетворяет ни одна точка плоскости, поскольку левая часть неотрицательна, а правая отрицательна при любом значении z. Говорят, что это уравнение есть уравнение окружности мнимого радиуса iR с действительным центром S, имеющим комплексную координату s=-b.

• 4. Когда , но , уравнение (16) противоречиво: левая часть его действительна, а правая нет. В этом случае оно не задает никакого геометрического образа (даже мнимого!).
• 5. Осталось рассмотреть случай, когда . Тогда из уравнения (15) вычтем уравнение , получающееся из (15) переходом к сопряженным комплексным числам. Получаем:

Выполняя эту подстановку в уравнение (15), приводим его к виду:

При уравнения (15) и (19) равносильны. В зависимости от того, отличен от нуля или равен нулю дискриминант:

квадратного уравнения (19), оно будет определять две различные (действительные!) или две совпавшие точки. При D=0 совпавшие точки имеют комплексную координату:

В частности, при c=ab как уравнение (16), так и уравнение (19) дает пару точек z₁=-b и .

Итак, уравнением (15) задается либо окружность (действительная, мни мая, нулевого радиуса), либо две точки (различные или же совпавшие), либо пустое множество точек.

Рассмотрим одну замечательную пару окружностей.

Две пересекающиеся окружности называются ортогональными, если касательные к ним в их общей точке перпендикулярны. Тогда, очевидно, касательная к одной из ортогональных окружностей в их общей точке содержит центр другой окружности.

Для того чтобы окружности (A, R) и (В, r) были ортогональны, необходимо и достаточно, чтобы |AB| 2 =R 2 +r 2 , или:

Если окружности заданы уравнениями:

то , и поэтому критерий (20) их ортогональности трансформируется так:

Решение задач

Задача 1. Хорды АВ и PQ окружности пересекаются в точке С. Найти множество точек М пересечения прямых АР и BQ, если точки А, В, С постоянны, а точки Р и Q пробегают данную окружность (рис.3).

Решение. Пусть z — комплексная координата произвольной точки М искомого множества и данная окружность принята за единичную . В силу зависимости координат точек, принадлежащих секущей к окружности (см. предыдущую статью), имеем:

откуда . Подставляя эти выражения во второе равенство, получаем:

Привлекая , полученному уравнению придадим вид:

Теперь ясно, что искомое множество точек представляет собой пару прямых, одной из которых является прямая АВ, а другая имеет уравнение:

в приведенной форме. Как видим, эта прямая не зависит от хорды АВ, а определяется лишь окружностью и точкой С. Она называется полярой точки С относительно окружности .

Задача 2. Около окружности описан квадрат ABCD. Точки — ортогональные проекции его вершин A, В, С, D соответственно на произвольную касательную к окружности. Доказать, что:

Решение. Радиус окружности примем за единицу длины. Систему координат выберем так, чтобы точки касания сторон АВ, ВС, CD, DA с окружностью имели координаты . Тогда вершины А, В, С, D будут иметь координаты Касательная к окружности в ее произвольной точке Р (р) имеет уравнение в приведенной форме. Руководствуясь формулой (13), находим:

Задача 3. Вершины A и В прямоугольного равнобедренного треугольника АВС спроектированы параллельно некоторой прямой l на прямую, проходящую через вершину С прямого угла, соответственно в точки и . Доказать, что сумма зависит только от угла между осью проекций и прямой l (при заданном треугольнике АВС).

Решение. Примем ось проекций за действительную ось х и вершину С за начало О. Прямую l проведем через О и зададим принадлежащей ей точкой Р(р), |p|=1. Ее уравнение имеет вид. Если вершина A имеет координату а, |а|=1, то вершине В соответствует число ai (рис.4).

Прямые АА₁ и BB₁ получают уравнения и . Для точек, лежащих на оси х проекций,. Подстановкой в предыдущие уравнения получаем координаты точек А₁ и В₁:

где — указанный в условии задачи угол..

Задача 4. На окружности взяты четыре произвольные точки А, В, С, D. Окружности соответственно с центрами A, В, С и проходящие через точку D пересекаются вторично попарно в точках (рис.5). Доказать, что точки коллинеарны.

Решение. Пусть окружность является единичной и точка D имеет координату d=l. Используя уравнение (14) и тот факт, что окружность имеет центр A(а) и содержит точку D(1), получаем ее уравнение:

Аналогично окружности и будут иметь уравнения:

Решая систему уравнений окружностей и , находим координату второй общей точки М3 этих окружностей: m3=a+b-ab.

Это число сопряжено самому себе, и потому точки коллинеарны.

Задача 5. Найти множество центров окружностей, проходящих через данную точку М (т) ортогонально данной окружности .

Решение. Если окружность обладает заданным свойством, то:

Исключая получаем уравнение относительно :

Им определяется прямая с нормальным вектором , который равен вектору , где — центр данной окружности. Следовательно, эта прямая перпендикулярна прямой AM (рис.6).

Видео:Изобразить область на комплексной плоскостиСкачать

КРИВЫЕ И ОБЛАСТИ В КОМПЛЕКСНОЙ ПЛОСКОСТИ

Видео:Окружности на комплексной плоскостиСкачать

Пути и кривые в С

В некоторых разделах математики важную роль играет понятие пути. Путь в топологическом (например, метрическом) пространстве X — это непрерывное отображение отрезка действительной оси (обычно это отрезок [0; 1 ]) в X. В случае X = С путем / будем называть непрерывное отображение отрезка [а;/?]-»С. Иными словами путь в комплексной плоскости есть комплекснозначная функция z = /(/) действительного переменного, непрерывная в каждой точке /₀ е[а;/?]. Непрерывность в такой точке понимается в следующем смысле: для любого е > 0 существует окрестность</ е[ог;/?]:|/-/ ₀| С лежит на множестве М сС, если y(t) eMVte. [а; /?]. Путь проходит через точку z е. С, если z = y(t) при некотором / е [а; /3].

Положительное направление пути у определяется направлением движения точки /(/) при возрастании / от а до /?. Переход от пути y:z = (p(t G[a,p к пути у

то его носителем является окружность единичного радиуса с центром в начале координат, пробегаемая против хода часовой стрелки. Путь у

задается формулой z = cos/-/sin/; его носителем является та же окружность, но пробегаемая по ходу часовой стрелки (сделайте чертежи!).

называются эквивалентными (и это обозначается символом у_х

у₂ ), если существует непрерывная строго возрастающая функция

осуществляющая отображение «на» (т.е. сюръективное), такая, что

Соответствующая графика изображена на следующем схематическом рисунке (рис. 4).

Функцию г(/) называют идентификатором путей у_х,у₂. Говорят, что путь у₂ получен из у_х заменой параметра (2.1).

Пример 2.1. Рассмотрим пути

Носитель всех путей один и тот же — это отрезок [0;1] действительной оси в С. Но лишь первые два мути эквиваленты с идентификатором г = arcsin/. Третий и четвертый пути им не эквивалентны и не эквивалентны друг другу — в них отрезок [0;1] обходится иначе, чем в первых двух. Но очевидно, что пути /,,/₂ эквивалентны Уу. Убедитесь в этом, выполнив соответствующие рисунки.

Нетрудно проверить, что отношение

удовлетворяет обычным аксиомам эквивалентности: рефлексивности, симметричности и транзитивности. Поэтому множества путей разбиваются на классы эквивалентности.

Класс эквивалентных путей называется кривой в С или плоской кривой. Для ее задания достаточно указать один из путей, остальные пути класса могут быть получены из указанного заменой параметра (2.1). О каждом из путей класса говорят, что он задает параметризацию кривой (ее уравнение).

Таким образом, в понятие кривой включается то общее, что имеется у соответствующих эквивалентных путей: одно и то же множество точек плоскости, принадлежащих любому из путей класса, определяющего кривую, и упорядоченность точек на кривой. Заметим, что понятие кривой не всегда согласуется с нашим интуитивным представлением о ней. Например, отрезок [0;1] действительной оси С, проходимый от 0 до 1 и затем обратно, есть замкнутая кривая (четвертый путь рассмотренного выше примера). Поразителен пример кривой Пеано — существование непрерывного отображения отрезка на квадрат!

Подчеркнем, что нс следует смешивать понятие кривой с множеством точек, через которые эта кривая проходит. Согласно введенному определению кривой оно включает в себя еще и порядок прохождения точек. Может оказаться, что одна и та же точка плоскости отвечает нескольким точкам кривой. В этом случае говорят, что кривая имеет точки самопересечения (кратные точки). Наглядно кривую можно представить в виде спутанной нитки, лежащей на плоскости.

Часто под кривой понимается образ отрезка при непрерывном отображении, но на отображение налагают некоторые дополнительные ограничения. Среди них выделим те, которые обладают свойствами, используемыми в дальнейшем. Заметим, что в литературе соответствующая терминология весьма разночтимая. Здесь и далее используются следующие термины.

Путь у z = x(t) + iy(t) (/ g [or;/?]) (функции x(t),y(t) действительнозначные) называется жордановым путем (или простой дугой), если отображение у взаимно однозначное. Если оно взаимно однозначное на промежутке (or;/?] и у(а) = у(Р), то говорят, что / есть замкнутый жорданов путь. Например, рассмотренные выше пути У,у₂>Уз жордановы, у₄ -нет.

Путь y:z = x(t) + iy(t)(te[a;0]) называется непрерывно дифференцируемым, если существует непрерывная производная y ) = x f <t) + iy l (t)на [а;/3]. На концах отрезка она односторонняя; в случае замкнутого пути еще предполагается, что у (а+ 0) = у (/3-0). Указанный путь называется гладким, если он непрерывно дифференцируемый с отличной от 0 производной. Это условие вводится обычно для того, чтобы в каждой точке носителя пути можно было бы провести касательную. При этом, если у'(/) = 0,У(Г)^0, то касательная параллельна оси абсцисс; при у (t) * 0, х (t) = 0 она параллельна оси ординат. Если же у =0, т.е. при некотором значении параметра обе производные х (!),/ (/) нулевые, то для углового коэффициента касательной

будет неопределенность вида Ц, поэтому касательной может и не быть. В качестве примера рассмотрим путь y:z(t) = 0 при / = 0, z(t) = t 2 +it 3 sin— при

0 0, но этот предел не существует (почему?).

Путь y:z = x(t) + iy <t)(te.[aPY)называется кусочно гладким, если задающая функция непрерывна на отрезке [а;/?] и его можно разбить на конечное число отрезков, на каждом из которых сужение у определяет гладкий путь. Докажите, что у :z = cost +/sin/, / е[0;2;г] есть замкнутый жорданов гладкий путь, а дуга полукубичсской параболы Нсйля y:z = t 2 +/7 3 ,/ е [—1;1] — жорданов непрерывно дифференцируемый путь, не являющийся гладким. Об этом свидетельствует рисунок параболы, который мы умышленно не приводим, предоставляя его выполнить читателю.

Такие же ограничения можно ввести и на кривые. Жорданова кривая — это класс путей, эквивалентных некоторому жорданову пути (так как замены параметров (2.1) взаимно однозначны, то из жордановости пути следует жор- дановость всех эквивалентных ему путей).

Определение гладкости кривой требует некоторых уточнений: мы должны ввести это понятие так, чтобы оно не нарушалось при замене пути, представляющего эту кривую, любым другим эквивалентным ему путем. Так как непрерывная и возрастающая замена параметра (2.1) может гладкий путь перевести в негладкий, то понятие гладкости не инвариантно по отношению к таким заменам. Поэтому на преобразование (2.1) наложили дополнительные условия. Именно, гладкой кривой называется класс путей, получающихся из некоторого гладкого пути всевозможными заменами параметра (2.1), где идентификатор г — непрерывно дифференцируемая функция с положительной производной. Аналогично поступают при определении кусочногладкой кривой — требуют, чтобы допустимые замены параметров имели непрерывную положительную производную всюду, кроме, может быть, конечного числа точек, в которых существуют односторонние производные.

Примером кусочно-гладкой кривой является кривая, заданная уравнением z = / + i|/|,/€[-l;l] (сделайтерисунок!).

Из курса теории функций действительного переменного следует помнить следующую теорему Жордана: для того, чтобы кривая

была спрямляемой (т.е. имела конечную длину), необходимо и достаточно, чтобы обе функции x(t), y <t)имели ограниченные вариации на отрезке

Оказывается, что гладкая кривая спрямляемая, и этот факт справедлив для кусочно-гладкой кривой.

В заключение этого параграфа в свете описанной терминологии охарактеризуйте (сделав рисунки) следующие пути и кривые.

📹 Видео

ТФКП. Линии и области на комплексной плоскости #shorts #mathСкачать

Область на комплексной плоскости arg z = pi/2Скачать

Область на комплексной плоскости. Re z^2=-1. ГиперболаСкачать

Множества на комплексной плоскости. Связное множество. Односвязная область. Граница. Круг сходимостиСкачать

Построение областей по заданным условиямСкачать

Стереографическая проекция. Расширенная комплексная плоскостьСкачать

ТФКП. Вычислить интеграл от функции комплексного переменного по данной кривой. Дуга окружности.Скачать

Найдем определенный интеграл, используя контурный в комплексной плоскостиСкачать

Область функции комплексной переменнойСкачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Конформные отображения с помощью линейной функцииСкачать

Тригонометрическая форма комплексного числаСкачать

ТФКП. Вычислить интеграл от функции комплексного переменного по данной кривой. Задан отрезок прямой.Скачать

ТФКП. Интеграл от функции комплексного переменного. Интегралы по различным путям.Скачать

Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Попов В. Ю. - ТФКП - Вычисление интегралов от функции комплексной переменной по кривойСкачать